如何解决该等式的线通过的两点?
数学不是一个无聊的科学,因为它似乎的时候。 它有很多有趣,虽然有时令人困惑,对于那些不渴望。 今天,我们将谈论中的一个最常见和最简单的主题,在数学,并更具体地说该地区是在边缘的代数和几何形状。 谈谈关于直接和他们的公式。 这似乎是一个无聊的学校问题,没有承诺什么有趣的和新的。 然而,它不是,并且我们将在这篇文章中试图证明我们的观点。 在行动之前以最有趣,描述公式线通过的两点,我们来的历史所有的这些测量,然后找出为什么它是一切必要的,为什么现在也不会干扰知识的随后的公式。
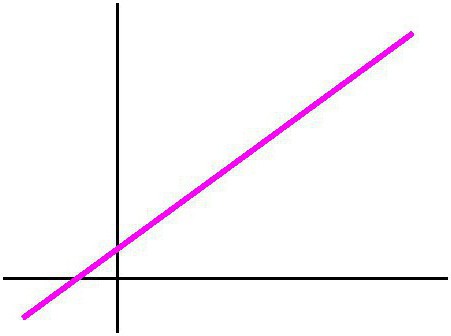
历史
在古代,数学家们喜欢的几何结构和各种图表。 它是困难的,今天说谁首先提出了公式线通过的两点。 但我们可以假设,这名男子是欧几里德,希腊的科学家和哲学家。 这是谁,他在他的论文"开始"给了基础上对未来的欧氏几何形状。 现在,这个分支的数学被认为是骨架的一个几何代表性的世界,发生在学校。 但是说,欧氏几何形状是否有效只有在宏观一级,在我们的三个方面。 如果我们考虑空间,这并不总是能够本着所有的现象发生在那里。
后,欧几里德还有其他的科学家。 和他们改善,并osmislili什么他发现和写。 最后,它变成了稳定的几何形状,这一切仍然是完整的。 和几千年来实践证明,该公式线通过的两点是非常容易和简单。 但在此之前进行解释如何做到这一点,讨论一点点的理论。
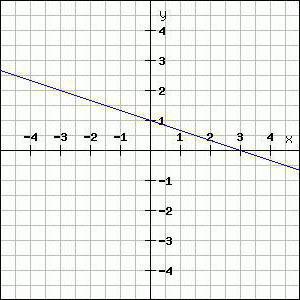
理论
线是无限两个方向的一段,可以分为一个无限的段数的任何长度。 为了提供直接、经常使用的图形。 此外,图形可以是两维和三维坐标系统。 他们是建立根据的坐标点举行。 毕竟,如果我们考虑直接的,你会发现,它包括无数的要点。
然而,有一些视频是非常不同于其他类型的线。 这是它的公式。 一般这是非常简单,不同,比如说,从圆形式。 当然,我们每个人举行了他在高中。 但我会把它写的一般形式:y=k+b。 在下一节中,我们详细分析每个什么这些信件以及如何解决的简单的公式线穿过了两点。
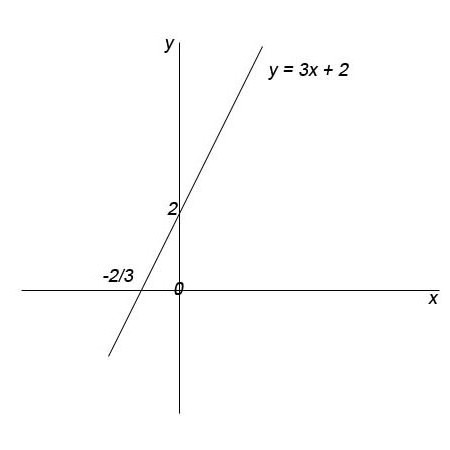
式的行
的平等,这是上文提及的是,我们有必要的公式线。 有必要澄清在这里,它意味着什么。 正如你可能猜测,y,x是每个点的坐标属于一条直线。 在一般情况下,该公式,只有存在,因为每个问题的任何线往往是在与其他连接点,因此有一项法律,结合一个协调与另一个。 该法确定的公式线通过两个给定点。
为什么两点? 所有这一切都是因为最小的点数需要建造一条直线在两个维空间,则等于两个。 如果我们采取三维空间中的点数需要建立一个单独的直以及为等于两个,三点已经做飞机。
还有一种理论证明,通过任何两点是能够进行直接的。 这一事实可以测试通过连接线的两个随机的点图。
现在考虑的一个具体实例和显示如何解决这个臭名昭着的等式线穿过两个给定点。
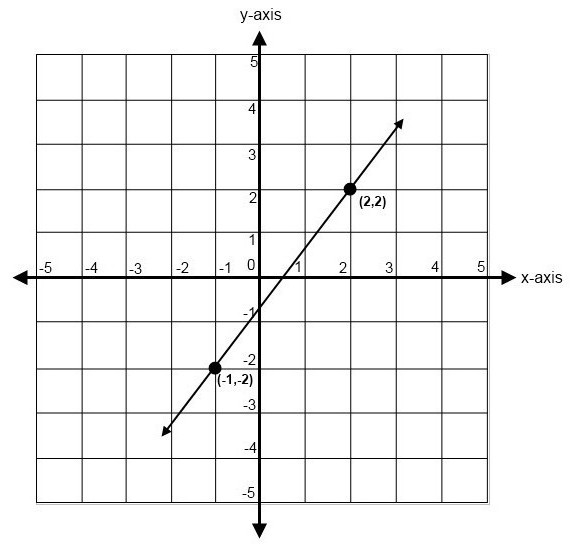
例
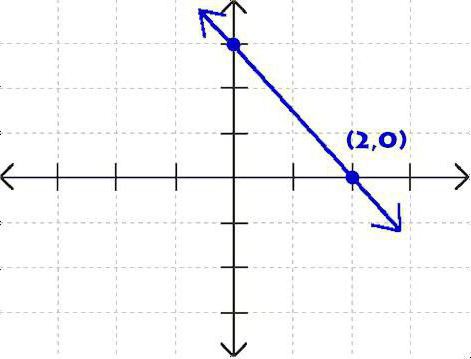
考虑的两点之间要建立直。 问问他们的坐标,例如,M<子>1(2;1)和M<子>2(3;2). 因为我们知道从学校课程,第一坐标值在牛轴线和第二轴线OY。 已给予上述公式线通过的两点,并使我们能够了解丢失的参数k和b,我们需要有一个系统的两个方程式。 事实上,它是由两个方程,这将是我们两个未知constants:
1=2k+b
2=3k+b
现在它仍然是最重要的是:解决这个系统。 这样做是相当简单。 开始快速从第一个方程式b:b=1-2k。 现在有必要的替代得到平等进入第二等式。 这是通过更换b中的公式:
2=3k+1-2k
1=k;
现在,我们已经学会了什么是系数的值k的,它的时间来学习的价值下面的恒-b。 这样做更容易。 因为我们知道的依赖b k,我们可以替代的最后价值中的第一个方程式来找到一个未知的价值:
B=1至2*1=-1.
知道这两个系数,现在可以替代他们在原来的一般性公式线通过两点。 因此,对于我们的示例,我们得到这个方程式:y=x-1。 这是所期望的平等,这是我们应该。
在进行之前的结论,我们将讨论的相关性这个主题的数学中的日常生活。
使用
如,应用程序的公式线通过的两点。 但是,这并不意味着它不是必要的。 在物理和数学是非常积极地使用的公式和性质它们所产生的。 你甚至可能不注意到,但数学是我们周围。 而即使是这样,乍一看,在不起眼的主题作为该公式线通过两点,是非常有用和非常频繁使用的一个基本的水平。 如果乍一看,这似乎是无处可能是有用的,你错了。 数学发展的逻辑思维,这绝不会伤害。
结论
现在,我们已经想出了如何建立直根据两点,我们不需要回答每一个问题与此相关联。 例如,如果老师对你说,"<跨>写的公式线穿过两点",那么你会不会很难这样做。 我希望这篇文章是对你有用。
Article in other languages:

Alin Trodden - 文章作者、编辑
"你好,我是艾琳*特罗登。 我写文章,看书,寻找印象。 我也不擅长告诉你这件事。 我总是乐于参与有趣的项目。"
相关新闻
之前,每个学生的毕业生从11类,有一种选择的哪所学校去学习。 学生,有目的、充满自信并希望获得市场需要的技能,邀请,卡卢加州大学。 齐奥尔科夫斯基。的简要信息有关的大学卡卢加州大学家庭债务还清;高等教育机构操作的在卡卢加自1948年以来。 早些时候,该大学教学的,但他后来成为经典。 此外,教育能力,还有其他的培训领域有关的不同领域的生活。[rek1]目前卡卢加州大学的一个主要在卡卢加地区。 它决定了它的发展,被认为是一个领导人之间的当地教育机构在该领域的高...
如何往往有你遇到的人以前缀的名字、姓氏或父"*阿里勒扎*奥格雷*". 但你有没有想过那意味着"*阿里勒扎*奥格雷*"? 今天,我们会回答这个问题从历史和法律的观点。原产地名称为"*阿里勒扎*奥格雷*"祖先古老的土耳其人的祖先对许多东欧国家。 这是习惯称的第一出生的男性"*阿里勒扎*奥格雷*",其翻译的意思是"儿子"。 后来的名称改为父姓或名称的子孙后代。 因此,批评男孩的名字"*阿里勒扎*奥格雷*"意味着它属于男人的儿子他的父亲。[rek1]怎么名字"*阿...
在任何语言可以找到词语,其含义是不明确的,甚至当你把它分解成部分。 例如,采取一词含义的"想像". 它是否与名词"楔子"? 如果是,它是如何改变时,你将前缀"za"?的词汇词含义的"想像"你可能会感到惊讶,但对名词"楔子"动词"za-克林-ing"没有任何关系。词的含义"召唤":尝试征服任何对象,他将通过神奇的力量:"不干扰,该法师旅行车联想到的一个墓碑躺在保护一个古老的宝藏"。征求或乞求在名称的东西的圣洁,重要的是,"大哥,我求求你的名称我们神圣的母亲:...
音乐占有重要地位,在人的生命。 一首好歌能让你振作起来伤心的时候,与她离去。 通过歌曲表达自己的情绪。 因此,没有什么令人惊讶的事实,谚语和语录音乐有在民间艺术。的歌曲谚语音乐是多种多样的。 他们说,不仅对歌曲,但也提到乐器。 也频繁提及的鸟类,这并不奇怪,因为他们的鸣叫让人联想到的旋律。"谈话的方式花费,而这首歌-的工作"-为什么人们常常开始对话与同胞的游客? 因为有趣的谈话时间飞过。 作为工作人员并不总是有机会说话的人,唱自己的人可以。 和快乐的歌曲,...
帕斯捷尔纳克一个最聪明和最有争议的作家第一半的20世纪。 他的诗都有一个哲学定向。 他早期的诗是简单明了,没有隐藏的含义。 但在同一时间,他们中的一些感觉到的影响的象征意义。 "定义的诗歌"帕斯捷尔纳克的分析,这是下文提出的,是试图提交人了解的目的诗歌。一些关于特征的创造力分析"的定义诗歌"帕斯捷尔纳克是最好开始介绍创作这个作家。 形成他的文学事业陷于艰难的岁月里,为国家。 在那个时候,许多创造性的人们沉迷于哲学思考。[rek1]不能保持冷漠的态度,从哲学...
语言的结构,因为如果该建筑建构的一个单独的目砖号;语言的单位,有的词汇的价值。 这些单位素和研究的支的语言学称为morphemics. 和文字的形成,作为一个较大的区域的语言,包括本身。有什么话?不管是什么字,我们没有探讨,这包括素家庭债务还清的一个或更多。 例如,在释放,目的菜单号;只有1素家庭债务还清的根源,这一形容词有何影响;在/吸引/a/teln/OE号;他们5:前缀,根,后缀,并且两个结束。Morphemics(和文字的形成作为主题的语言)的定义...



















评论 (0)
这篇文章没有评论,是第一!