Now - 21:10:19
A superfície da ordem de 2: exemplos
Com superfícies de 2ª ordem estudante, que é mais comum no primeiro ano. Primeiro, tarefas sobre este assunto, podem parecer simples, mas, à medida que o estudo de matemática e aprofundamento na pesquisa de lado, você pode finalmente parar de navegar na atividade. Para tal não aconteceu, é preciso não apenas memorizar e entender como é que um ou o outro superfície, como uma alteração de probabilidades afeta ela e sua localização em relação ao original, o sistema de coordenadas e como encontrar o novo sistema (aquele em que o seu centro coincide com o início de coordenadas, e o eixo de simetria paralelo a um dos eixos de coordenadas). Vamos começar desde o início.
Definição
A Superfície 2, a ordem é chamado ГМТ cujas coordenadas satisfazem a equação geral é semelhante ao seguinte:
F(x,y,z)=0.
é Claro que cada ponto pertencente a superfície, deve ter três coordenadas em qualquer identificada como linha de base. Embora, em alguns casos geométrica lugar de pontos pode degenerar, por exemplo, em um plano. Isso só significa que uma das coordenadas é constante e igual a zero em toda a área de valores válidos.
Total pintados à forma mencionado acima, a igualdade parece так:
A11X2+A22Y2+A33Z2+2A12Xy+2A23Yz+2A13Xz+2A14X+2A24Y+2A34Z+A44=0.
ANm – algumas constantes, x, y, z – as variáveis responsáveis аффинным coordenadas de qualquer ponto. Quando o fizer, pelo menos, um dos multiplicadores constantes deve ser igual a zero, ou seja, não há qualquer ponto de responder equação.
A grande maioria dos muitos exemplos numéricos multiplicadores ainda são identicamente iguais a zero, e a equação é bastante simplificada. Na prática, a definição pessoal de um ponto à superfície não é difícil (o suficiente para substituir as suas coordenadas na equação e verificar o que é observado se a identidade). O ponto-chave em tal trabalho é trazer a última a problemas de canonização.
Escrito acima, a equação especifica qualquer (todas as) da superfície de 2 ordem. Exemplos considere o seguinte.
Tipos de superfícies da ordem de 2
A Equação das superfícies de 2 ordem variam apenas os valores dos coeficientes ANm. O aspecto geral em determinados valores constantes podem resultar em superfícies diferentes, classificadas da seguinte forma:
- Cilindros.
- Tipo Elíptico.
- Hyperbolic tipo.
- Cónico tipo.
- Parabólico tipo.
- Avião.
Cada um destes tipos existem natural e o imaginário, a forma de: imaginária de forma geométrica lugar de reais pontos ou degenera em mais do que uma simples figura, está presente em tudo.
Cilindros
Este É o tipo mais simples, como é relativamente complexa a curva se encontra apenas na base, servindo como um guia. Compõem são uma reta perpendicular ao plano que contém a base.
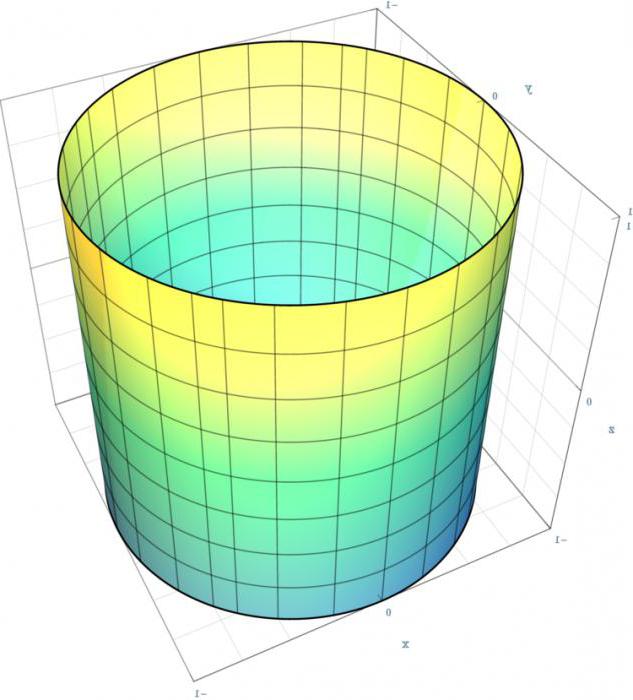
O gráfico mostra um cilindro circular – um caso particular do cilindro elíptico. No plano XY sua projeção será эллипсом (no nosso caso - round) - guia, e na XZ – um retângulo – assim como o compõem paralelas ao eixo Z. Para obtê-lo a partir de uma partilha de equações, é necessário dar as probabilidades dos seguintes valores:
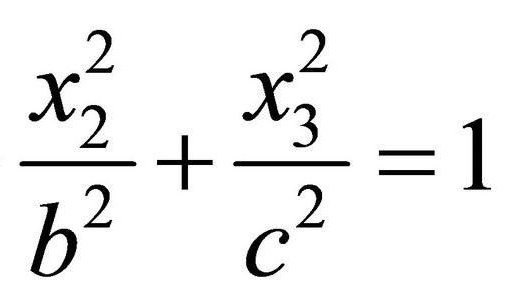
Em Vez do usual a notação x, y nós, jogo usado x com o número de série – isso não tem nenhum valor.
De fato, 1/a2 E estes aqui constantes são os mais probabilidades listados na equação geral, mas aceitou gravá-los exatamente como – é a representação canônica. Em seguida será exclusivamente utilizado este registro.
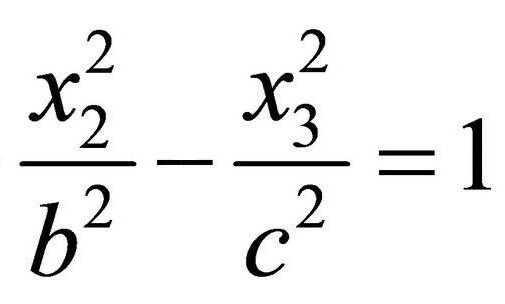
Define hyperbolic cilindro. O esquema é o mesmo – guia será hipérbole.
Y2=2px
O cilindro Parabólico é definido de forma um pouco diferente: a sua forma canônica inclui o fator p, chamado de parâmetro. Na verdade, o fator é igual a q=2p, mas aceito compartilhar sua apresentados dois multiplicador.
Há um outro tipo de cilindros: o imaginário. Esse cilindro não pertence nem a um real ponto. Ele descreve a equação do cilindro elíptico, mas em vez da unidade vale a pena -1.
Elíptico tipo
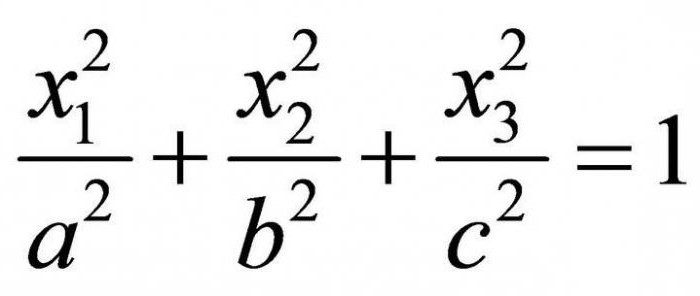
Elipsóide de referência pode ser esticado ao longo de um dos eixos (ao longo da qual seja, depende dos valores constantes a, b, c, acima, é óbvio que a maior eixo é atender o maior coeficiente).

Também existe e o imaginário elipsóide de referência – desde que a soma de coordenadas,multiplicado probabilidades é igual a -1:
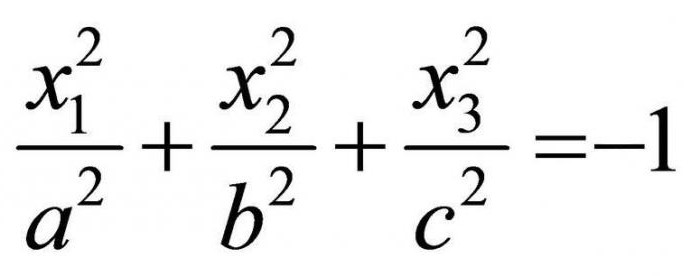
Гиперболоиды
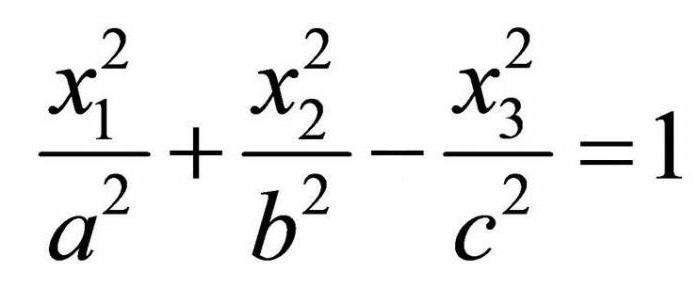
Quando aparecer o sinal de menos em uma das constantes, a equação do elipsóide se transforma na equação однополостного гиперболоида. Deve-se entender que este ponto não deve aparecer antes de uma coordenada x3! Ele apenas define qual dos eixos, o eixo de rotação гиперболоида (ou paralelo a ela, assim como quando lhe for mais termos ao quadrado (por exemplo, (x-2)2) desloca-se o centro da forma, como resultado, a superfície se move paralelamente aos eixos de coordenadas). Isso se aplica a todas as superfícies de 2 ordem.
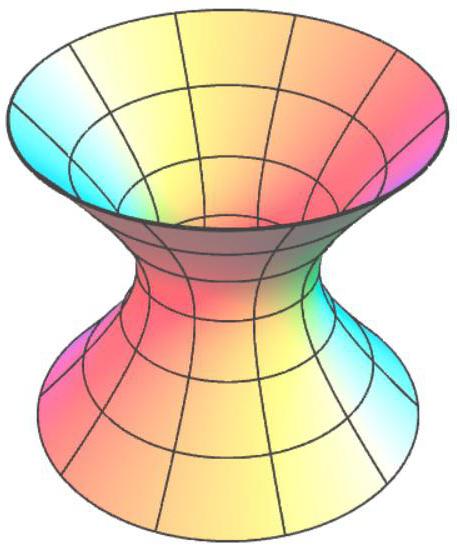
Além disso, deve-se entender que as equações são apresentados na forma canônica e eles podem ser modificados usando a variação de constantes (mantendo o sinal!); no entanto, a sua vista (гиперболоид, cone e assim por diante) permanecerá o mesmo.
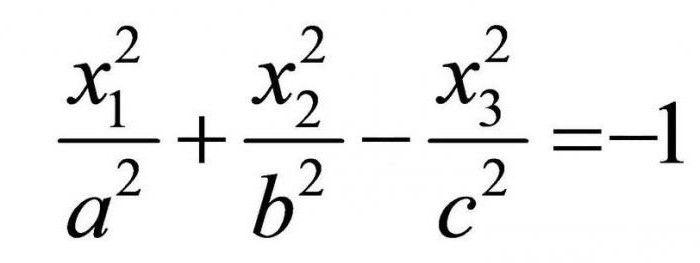
Esta equação define já двуполостный гиперболоид.
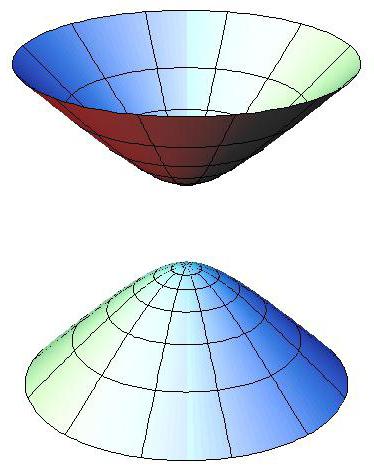
Superfície Cônica
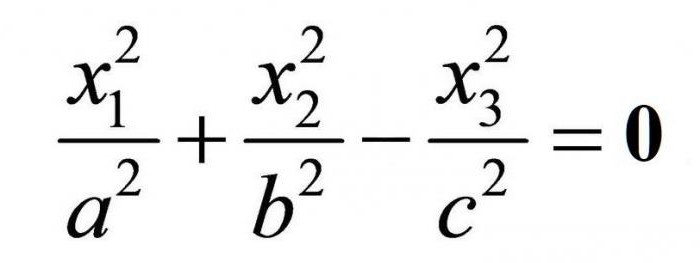
Na equação do cone unidade ausente – a igualdade a zero.
Cone chamado apenas limitada da superfície cônica. Na imagem abaixo, podemos ver que, de fato, o gráfico fica os dois chamados de cone.
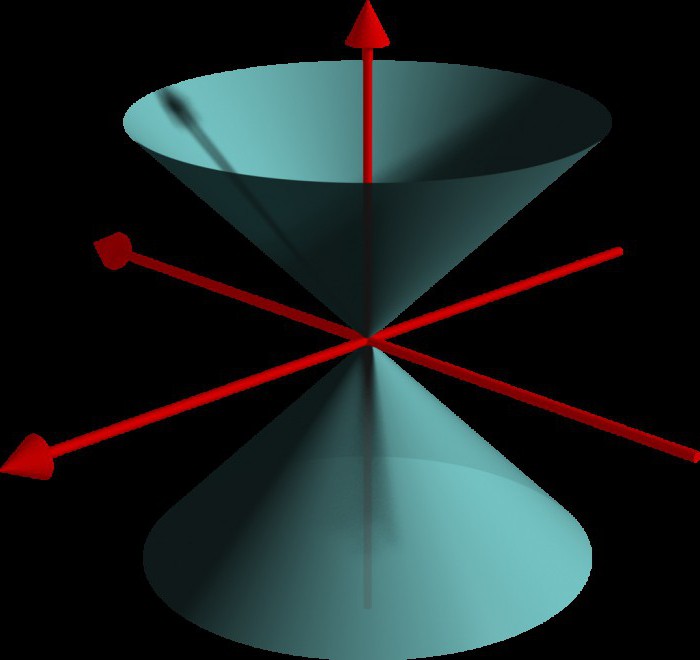
Nota Importante: todos os considerados canônicos, as equações constantes padrão aceito positivos. Caso contrário o sinal pode afetar o final do gráfico.
Eixos do plano tornam-se planos de simetria do cone, o centro de simetria está no início de coordenadas.
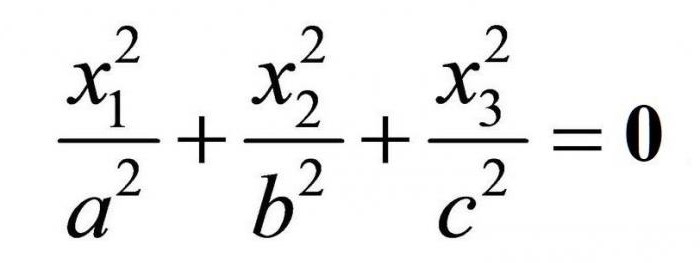
Na equação, o imaginário do cone custam apenas os profissionais; a ele pertence a um único real a ponto.
Параболоиды
A Superfície de 2 a ordem no espaço podem tomar uma variedade de formas, mesmo quando a equações semelhantes. Por exemplo, параболоиды são de dois tipos.
X2/a2+y2/b2=2z
Elíptico параболоид, quando a localização do eixo Z perpendicular com o desenho, a ser projetado em uma elipse.
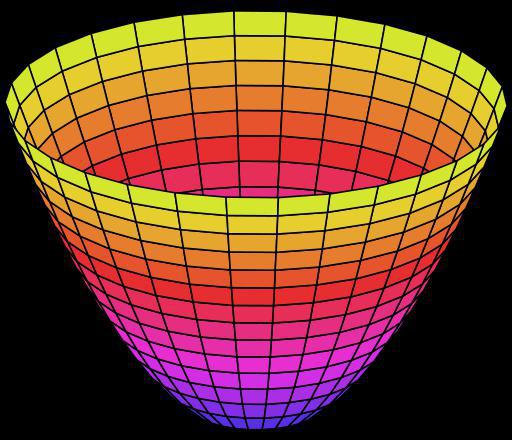
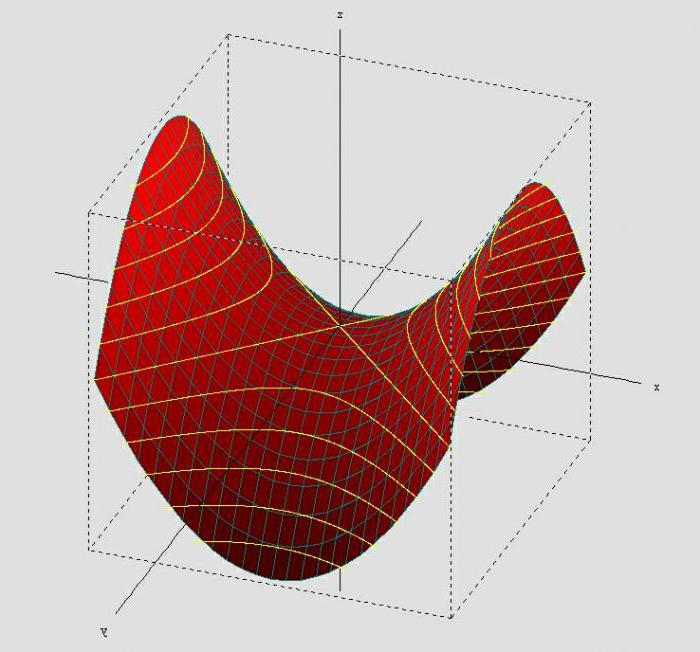
X2/a2-y2/b2=2z
Hyperbolic параболоид: em сечениях planos paralelos ZY, pode requisitar uma parábola, e сечениях planos paralelos XY – hipérbole.
Sobreposição de avião
Há casos em que a superfície de 2o ordem degeneram em um avião. Estes planos podem ser colocados de várias maneiras.
Primeiro, considere a intersecção do plano:
X2/a2-y2/b2=0
Quando tal modificação canônico da equação são obtidos apenas duas argolas de avião (imaginário!); todos os reais pontos estão localizados sobre o eixo da coordenada que está faltando na equação (em canônico – o eixo Z).
Faces Paralelas
Y2=a2
Se você tiver apenas uma coordenada da superfície de 2 ª ordem degeneram em um par de planos paralelos. Não se esqueça de, no lugar игрека pode ficar de qualquer outra variável; em seguida, será obtido plano, paralelo a outros eixos.
Y2=−a2
Neste caso, eles se tornam imaginários.
Correspondentes plano
Y2=0
Quando é tão simples equação de alguns planos de degenerar em uma – elas correspondem.
Não se esqueça de que, no caso tridimensional da linha de base é representada pela equação acima não define a reta y=0! Não há duas outras variáveis, mas isso apenas significa que o seu valor constante e igual a zero.
Criar
Uma das tarefas mais difíceis para o aluno é exatamente a construção de superfícies de 2 ordem. É ainda mais difícil de passar de um sistema de coordenadas para outro, considerando os ângulos de inclinação da curva relativamente eixos e um deslocamento do centro de. Vamos repetir, como consistentemente determinar o futuro de uma vista de desenho analítico maneira.
Para construir a superfície de 2 a ordem, a necessidade de:
- Levar a equação a problemas de canonização;
- Identificar a espécie pesquisada superfície;
- Construir, baseando-se em valores de coeficientes.
Abaixo são todos considerados tipos:
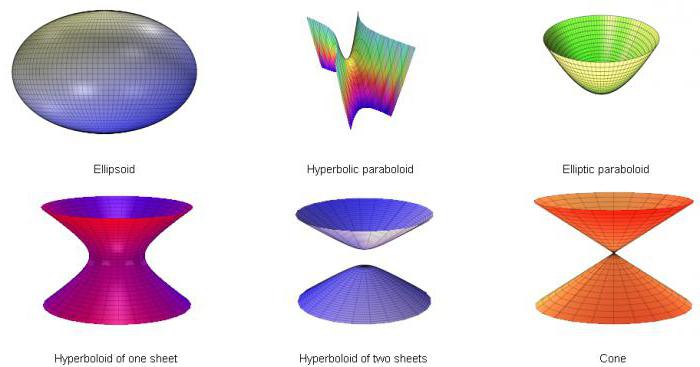
Para prender a detalhes распишем um exemplo desse tipo de trabalho.
Exemplos
Digamos que tem a equação:
3(x2-2x+1)+6y2+2z2+60y+144=0
Damos-lhe aproblemas de canonização. Destacam-se cheios de praças, ou seja, скомпонуем disponíveis soma de tal maneira que eles foram decomposição do quadrado da soma ou da diferença. Por exemplo: se a (a+1)2=a2+2a+1, então a2+2a+1=(a+1)2. Nós vamos passar a segunda operação. Parênteses neste caso, divulgar não necessariamente, pois isso só vai complicar a computação, e eis suportar multiplicador total 6 (faixa completa com o quadrado игрека), você precisa:
3(x-1)2+6(y+5)2+2z2=6
A Variável zat ocorre neste caso, apenas uma vez – você pode até não tocar em nada.
Analisando a equação nesta fase: antes de todos os desconhecidos vale a pena o sinal de "maisç a divisão em seis permanece unidade. Portanto, estamos diante de uma equação que represente o elipsóide de referência.
Note que a 144 foi decomposta em 150-6, depois -6 movido para a direita. Por que você tinha que fazer exatamente? Obviamente, o maior divisor neste exemplo, -6, portanto, para depois dividir por ele à direita, manteve-se a unidade, você precisará ão aguarde» a partir de 144 6 (sobre o que é direita deve ser a unidade, diz a disponibilidade de um membro – constantes, não vezes desconhecida).
Dividir todos os seis e obter a equação canônica elipsóide:
(x-1)2/2+(y+5)2/1+z2/3=1
é utilizada anteriormente, a classificação de superfícies 2 a ordem é considerada um caso particular, quando o centro da figura está no início de coordenadas. Neste exemplo, ele se inclina.
Acreditamos que cada um parêntese de fechamento com desconhecidos – é uma nova variável. Ou seja: a=x-1, b=y+5, c=z. Nas novas coordenadas do centro do elipsóide coincide com o ponto (0,0,0), portanto, a=b=c=0, onde: x=1, y=-5, z=0. Em originais coordenadas do centro da figura está no ponto (1,-5,0).
Elipsóide de referência será obtido a partir de duas elipses: primeiro no plano XY, e o segundo no plano XZ (ou YZ – isso não importa). Os coeficientes, em que são divididas as variáveis estão em canônico equação ao quadrado. Portanto, no exemplo acima, o correto seria dividir por raiz de dois, a unidade e a raiz de três.
Eixo Menor de primeira elipse, paralelamente ao eixo Y, é igual a dois. A maior eixo paralelo do eixo X – duas raízes dos dois. Menor eixo segunda elipse, paralelamente ao eixo Y, continua a ser a mesma – ela é igual a dois. E o maior eixo paralelo do eixo Z, é igual a dois raízes dos três.
Com a ajuda obtidos a partir da equação original através da conversão a problemas de canonização de dados podemos desenhar um elipsóide de referência.
Resumindo
Iluminado neste artigo, o assunto é bastante extensa, mas, na verdade, como você pode ver agora, não é muito complicado. Sua curva de aprendizado, de fato, termina naquele momento, quando você está aprendendo o nome e a equação da superfície (e, é claro, de como eles se parecem). No exemplo acima, detalhe da consideraram a cada passo, mas trazendo a equação a problemas de canonização requer o mínimo de conhecimento em matemática e não deve causar nenhuma dificuldade para os estudantes.
A Análise do futuro do gráfico de igualdade existente já é uma tarefa mais complexa. Mas para a sua solução perfeita o suficiente para entender o que são as correspondentes curvas de segunda ordem – elipses, parábolas e outros.
Casos de degeneração – ainda mais simples tópico. Devido à falta de algumas variáveis simplifica não só de computação, como já foi dito anteriormente, mas também a própria construção.
Uma vez que você pode certamente ser chamado de todos os tipos de superfícies, para variar constantes, transformando o gráfico em uma determinada forma – o tema será dominado.
Sucesso no treinamento!
Article in other languages:
PL: https://tostpost.com/pl/edukacja/38848-na-powierzchni-oko-o-2-przyk-ady.html
ZH: https://tostpost.com/zh/education/18836-surface-of-order-2-examples.html

Alin Trodden - autor do artigo, editor
"Olá, sou o Alin Trodden. Escrevo textos, leio livros e procuro impressões. E eu não sou ruim em falar sobre isso. Estou sempre feliz em participar de projetos interessantes."
Notícias Relacionadas
Onde foi a expressão "popa com o punho"?
A russa fala há muito divertidas e sustentáveis de expressões, que são bons e como беззлобная uma piada, e como bem-humorado censura. Um exemplo brilhante - "popa com o punho". De onde veio essa фразеологизм? O que quer dizer o ho...
as Questões ambientais, a teoria da evolução, популяционной de biologia e de outras ciências, muitas vezes afetam o conceito de variabilidade (como uma certa e incerta). Esta é a pedra angular para a compreensão da origem das espé...
A verificação e a exames de melhor, é claro, de se preparar. No entanto, você pode fazer sem ele. É sabido que bem decorada ucha pode fornecer até 85% de sucesso. Fazê-los – também é um trabalho, é uma espécie de prepa...
"A doutrina é a luz, e неученье trevas": o valor, o significado e as alternativas
Tem como ditados, que, aparentemente, não precisam de explicação, por exemplo, "doutrina – é a luz, e неученье – as trevas". Mas alguns não entendem o seu significado. Mas não só para essas pessoas, escrito p...
Ciências exatas – quais são eles
o Que são as ciências exatas? Pode-se dar algum tipo de clara de determinar-lhes, se todo o conhecimento tem a sua estrutura e características, suas teorias, leis e conceitos básicos. Com isto, exatas ciências agora chamam a...
A radiação ultravioleta e suas propriedades
a radiação Ultravioleta — é a radiação eletromagnética de comprimento de ondas, o qual varia de fronteira violeta do espectro, até o limite de raios-x. Vale ressaltar, que a primeira menção sobre esse fenômeno surgiu no sécu...



















Comentários (0)
Este artigo possui nenhum comentário, seja o primeiro!