Now - 06:20:19
Na powierzchni około 2: przykłady
Z powierzchniami 2-go rzędu student występuje najczęściej na pierwszym roku. Najpierw zadania na ten temat może wydawać się proste, ale w miarę nauki matematyki wyższej i zagłębienia się w naukową stronę, możesz w końcu przestać poruszać się w tym, co się dzieje. Aby do tego nie doszło, nie trzeba po prostu zapamiętać i zrozumieć, jak to jest ta lub inna powierzchnia, jak zmiana kursu wpływa na nią i jej położenie w stosunku do pierwotnej układu współrzędnych i jak znaleźć nowy system (taką, w której środek pokrywa się z początkiem układu współrzędnych, a oś symetrii jest równoległa do jednej z osi współrzędnych). Zacznijmy od samego początku.
Określenie
Powierzchni 2 około nazywa się zbiór punktów, którego współrzędne spełniają ogólnego równania podobny do następującego:
F(x,y,z)=0.
Jasne, że każdy punkt, należąca do powierzchni, musi mieć trzy współrzędne w jakimś wyznaczonym linią końcową. Chociaż w niektórych przypadkach zbiór punktów może się przerodzić, na przykład, w płaszczyznę. To tylko znaczy, że jedna ze współrzędnych jest stała i równa zeru w całym zakresie dopuszczalnych wartości.
Pełna rozpisany kształt wspomnianego wyżej równości wygląda так:
A11X2+A22Y2+A33Z2+2A12Xy+2A23Yz+2A13Xz+2A14X+2A24Y+2A34Z+A44=0.
ANm – niektóre stałe, x, y, z – zmienne odpowiedzialne аффинным współrzędnych żadnego punktu. Przy tym przynajmniej jeden z mnożników-stałych musi być równy zero, czyli nie każdy punkt będzie spełniać równanie.
W zdecydowanej większości przykładów wiele liczbowe mnożniki jednak tożsamość równe zero, a równanie jest znacznie uproszczone. W praktyce określenie przynależności punktu do powierzchni nie jest trudne (wystarczy podstawić jej współrzędne do równania i sprawdzić, czy przestrzegane tożsamość). Kluczowym momentem w takiej pracy jest doprowadzenie do ostatniej do kanoniczną myśli.
Napisane powyżej równanie określa wszelkie (wszystkie podane dalej) powierzchni 2 około. Przykłady rozważmy dalej.
Rodzaje powierzchni około 2
Równania powierzchni 2 około różnią się tylko wartościami współczynników ANm. Z ogólnego wyglądu przy określonych wartościach stałych mogą mieć różne powierzchnie, które zostały sklasyfikowane w następujący sposób:
- Cylindry.
- Typ Eliptyczny.
- Typ Hiperboliczny.
- Stożkowy typ.
- Paraboliczny typ.
- Płaszczyzny.
U każdego z wymienionych gatunków jest naturalna i jego forma: w wyimaginowanej postaci zbiór punktów materialnych albo przeradza się w bardziej prosty rysunek, albo nie ma wcale.
Cylindry
Jest To najprostszy typ, tak jak stosunkowo skomplikowana krzywa leży tylko w podstawie, występując jako prowadnicy. Tworząc są bezpośrednie, prostopadłe do płaszczyzny, w której leży założenie.
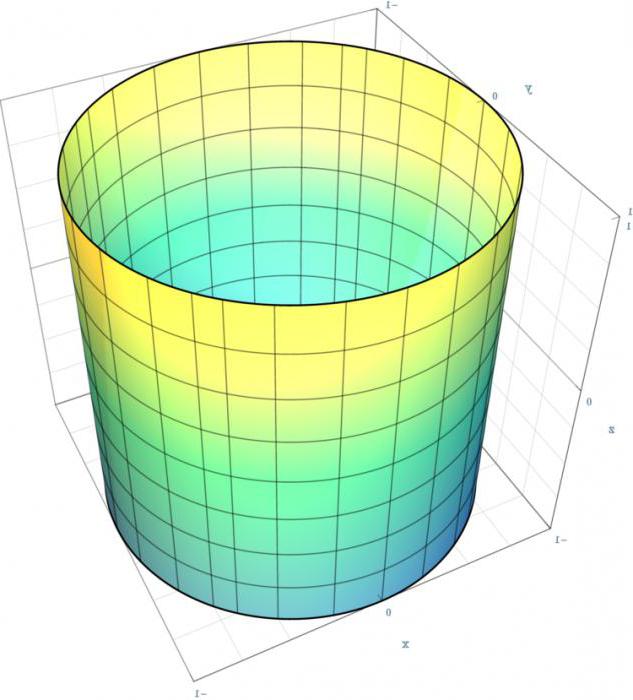
Na wykresie przedstawiono okrągły cylinder ó szczególny przypadek eliptycznego cylindra. W płaszczyźnie XY jego projekcja będzie эллипсом (w naszym przypadku około) - prowadnicy, a w XZ ó prostokątem – tak jak tworzą równoległe do osi Z. Aby dostać się z ogólnego równania, należy nadać kursy następujące wartości:
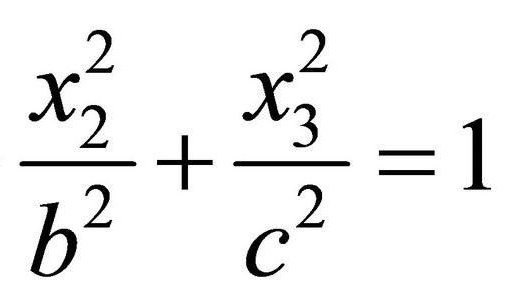
Zamiast zwykłych symboli x, y, zet wykorzystane иксы z kolejnym numerze – to nie ma żadnego znaczenia.
W istocie, 1/a2 I inne wymienione tutaj stałe są tymi samymi współczynnikami określonymi w ogólnym równaniu, ale w zwyczaju nagrywać je właśnie w takiej postaci – to jest kanoniczne przedstawienie. Dalej będą wykorzystywane wyłącznie taki zapis.
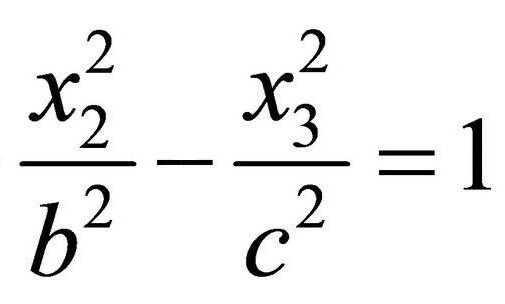
Tak określa hiperboliczny cylinder. Schemat ten sam ó prowadnicy będzie hiperbola.
Y2=2px
Paraboliczny siłownik ustawia się nieco inaczej: jego postaci kanonicznej zawiera współczynnik p, zwany parametrem. W rzeczywistości, współczynnik równy q=2p, ale przyjęto dzielić go na przedstawione dwa mnożenia.
Jest jeszcze jeden rodzaj silnika: urojone. Takiego cylindra nie należy żadna materialna punkt. Opisuje go równanie eliptyczne cylindra, ale zamiast jednostki warto -1.
Eliptyczny typ
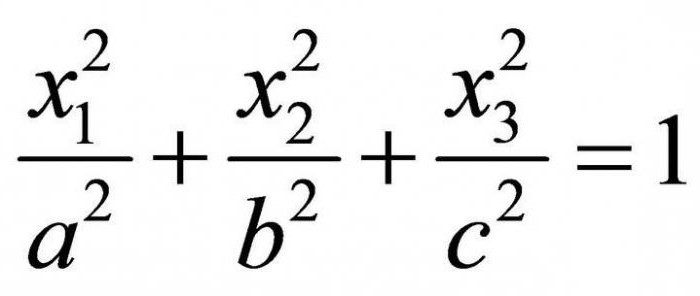
Elipsoida może być rozciągnięta wzdłuż jednej z osi (wzdłuż której właśnie zależy od wartości stałych a, b, c, o których mowa powyżej; jest oczywiste, że większą osi będzie pasował większy współczynnik).

Istnieje Także rzekomą elipsoida – pod warunkiem, że suma współrzędnych,помноженная na kursy, jest równa -1:
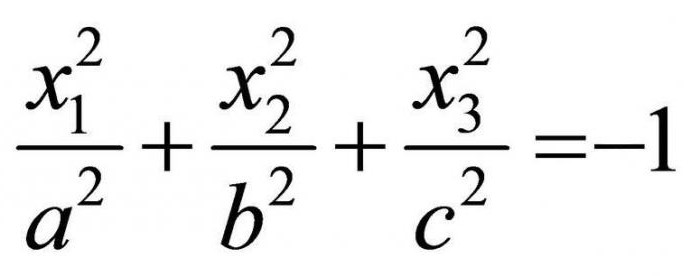
Гиперболоиды
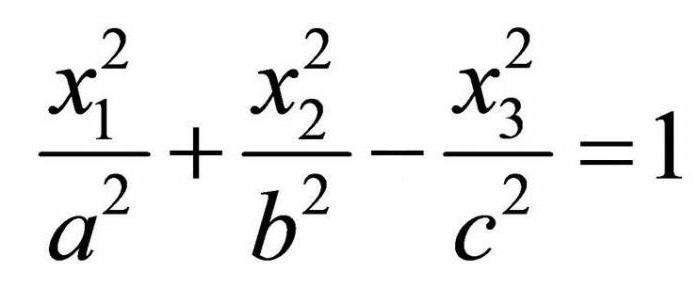
Gdy pojawi się minus w jednej ze stałych równanie elipsoidy przekształca się w równanie однополостного гиперболоида. Trzeba zrozumieć, że ten minus nie musi znajdować się przed współrzędną x3! On tylko określa, który z osi będzie osią obrotu гиперболоида (lub równoległa do niej, ponieważ po pojawieniu się dodatkowych terminów, w kwadracie (na przykład, (x-2)2) przesunięcie środka figury, w konsekwencji, powierzchnia przesuwa się równolegle do osi układu współrzędnych). To odnosi się do wszystkich powierzchni 2 rzędu.
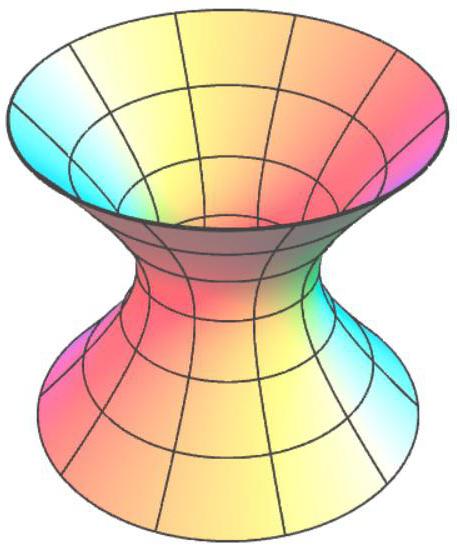
Poza tym, trzeba zrozumieć, że równania przedstawione w kanonicznym postaci i mogą być modyfikowane za pomocą zmienności stałych (z zachowaniem znaku!); przy tym ich wygląd (гиперболоид, stożek i tak dalej) pozostanie ten sam.
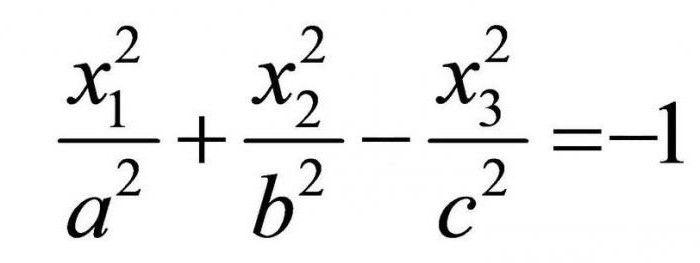
To jest równanie określa już двуполостный гиперболоид.
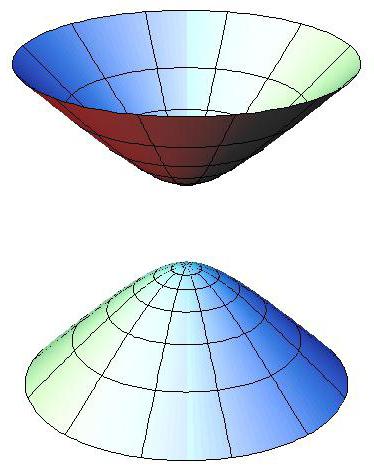
Stożkowa powierzchnia
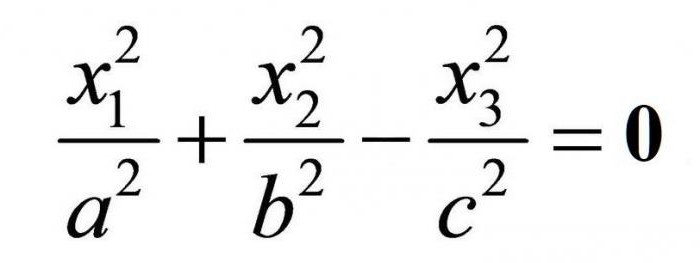
W równaniu stożka jednostka brakuje ó równość zero.
Stożkiem nazywa tylko ograniczona stożkowa powierzchnia. Na zdjęciu poniżej widać, że, w istocie, na wykresie okaże się dwa tzw. stożka.
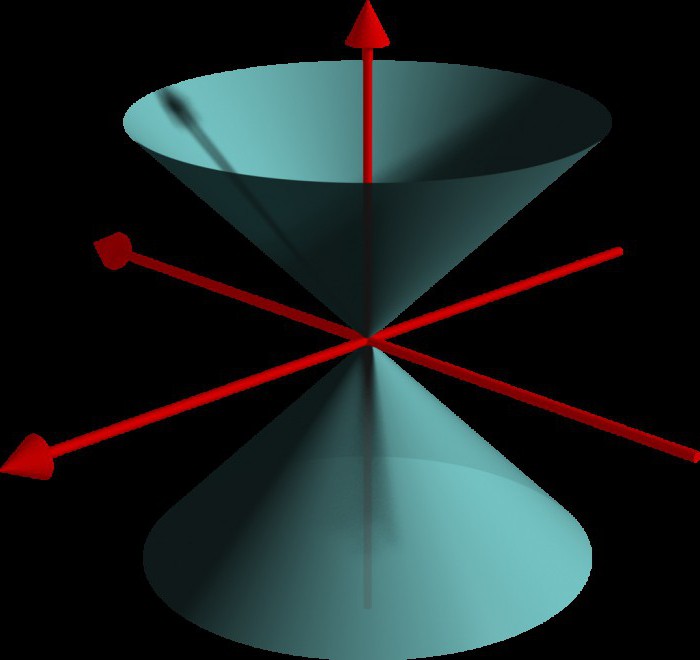
Ważne: we wszystkich rozważanych kanonicznych równaniach stałe domyślnie przyjmowane są pozytywne. W przeciwnym razie znak może mieć wpływ na końcowy wykres.
Płaszczyzny Xy są płaszczyznami symetrii stożka, centrum symetrii znajduje się w początku układu współrzędnych.
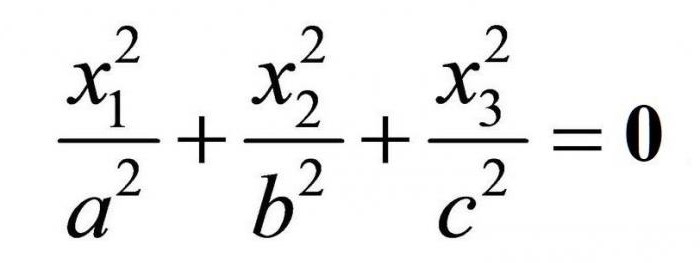
W równaniu rzekomego stożka są tylko plusy; należy do niego jedna jedyna materialna punkt.
Параболоиды
Powierzchni 2 porządku w przestrzeni mogą przybierać różne formy, nawet przy podobnych równaniach. Na przykład, параболоиды są dwóch rodzajów.
X2/a2+y2/b2=2z
Eliptyczny параболоид, w położeniu osi Z prostopadle do rysunku, będzie wyświetlany w elipsę.
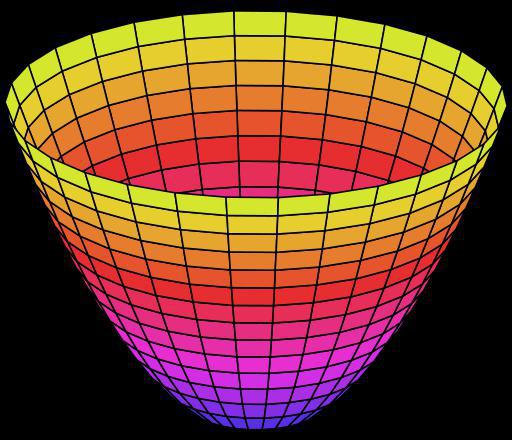
X2/a2-y2/b2=2z
Hiperboliczny параболоид: w przekrojach płaszczyznami równoległymi ZY, zostaną uzyskane paraboli, a w przekrojach płaszczyznami równoległymi XY ó hiperboli.
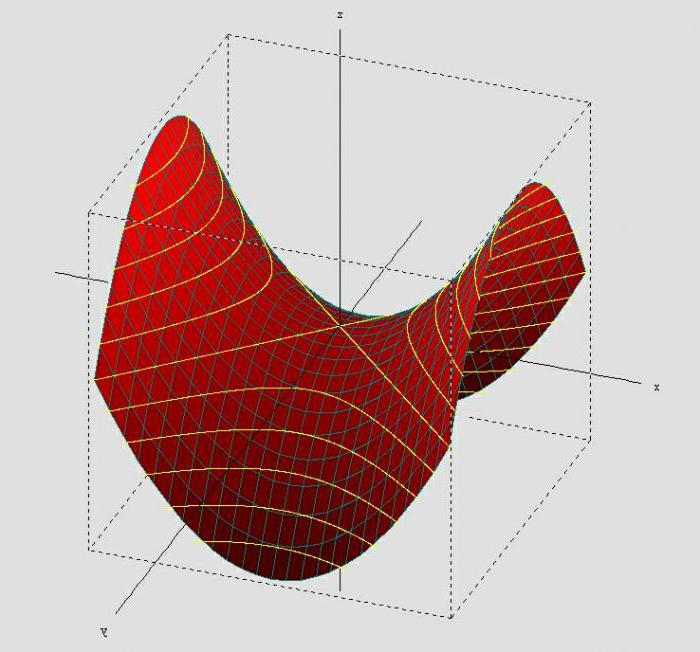
Przecinające się płaszczyzny
Istnieją przypadki, gdy powierzchnie 2-go rzędu degenerują się w płaszczyźnie. Te płaszczyzny mogą znajdować się na różne sposoby.
Rozważmy Najpierw przecinające się płaszczyzny:
X2/a2-y2/b2=0,
Przy takiej modyfikacji kanonicznej równania są tylko dwie przecinające się płaszczyzny (urojone!); wszystkie fizyczne punkty znajdują się na tej osi współrzędnych, który nie jest w równaniu (w kanonicznym ó osi Z).
Równoległe płaszczyzny
Y2=a2
Jeśli masz tylko jedną współrzędne powierzchni 2-go rzędu degenerują się w kilka równoległych płaszczyzn. Nie zapominaj, na miejscu игрека może stać jakaś inna zmienna; wtedy zostaną uzyskane płaszczyzny równoległe do innych osiach.
Y2=−a2
W tym przypadku stają się one wyimaginowane.
Pasujące płaszczyzny
Y2=0,
Przy takim prostym równaniu para płaszczyzn, co przeradza się w jedno – są one takie same.
Nie zapominaj, że w przypadku trójwymiarowego linii końcowej przedstawione powyżej równanie nie określa prostą y=0! W nim brakuje dwie inne zmienne, ale to tylko znaczy, że ich wartość jest stale i wynosi zero.
Tworzenie
Jednym z najtrudniejszych zadań dla ucznia jest właśnie budowanie powierzchni 2 około. Jeszcze bardziej trudne przejście z jednego układu współrzędnych do drugiego, biorąc pod uwagę kąty nachylenia krzywej względem osi i przesunięcie środka. Powtórzmy to, jak konsekwentnie określić przyszły wygląd rysunku analityczny sposób.
Aby zbudować powierzchnia 2 w porządku, należy:
- Doprowadzić równanie do kanoniczną myśli;
- Określić rodzaj badanej powierzchni;
- Budować, opierając się na wartości współczynników.
Poniżej znajdziesz wszystkie wspomniane rodzaje:
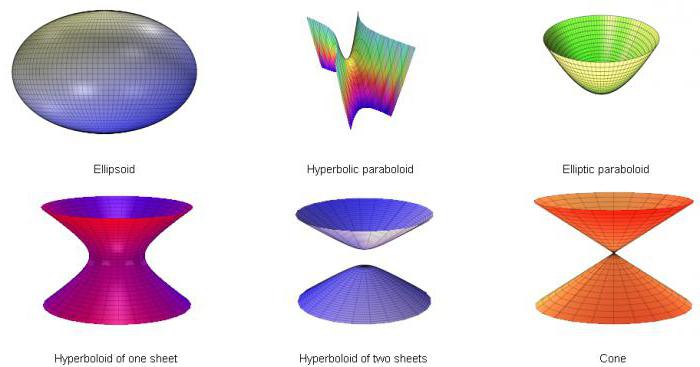
Do mocowania szczegółowo распишем jeden przykład tego typu zadania.
Przykłady
Załóżmy, że istnieje równanie:
3(x2-2x+1)+6y2+2z2+60y+144=0
Oto go dokanoniczną myśli. Podkreślić pełne kwadraty, czyli скомпонуем dostępne suma w taki sposób, aby były one rozkładem kwadratu sumy lub różnicy. Na przykład: jeśli (a+1)2=a2+2a+1, to a2+2a+1=(a+1)2. Zamierzamy przeprowadzić drugą operację. Nawiasy w tym przypadku ujawnienia nie koniecznie, tak jak to tylko komplikuje obliczenia, a to wydać wspólny mnożnik 6 (w wspornika z pełnym kwadratem игрека) należy:
3(x-1)2+6(y+5)2+2z2=6
Zmienna зэт spotyka się w tym przypadku tylko jeden raz ó można ją dopóki nie dotykać.
Analizujemy równanie na tym etapie: przed wszystkimi niewiadomymi stoi znak óplus»; przy podziale na sześć pozostaje jednostka. Zatem przed nami równanie, określająca elipsoida.
Zauważ, że 144 było ustanowione na 150-6, po czym -6 przeniesiono w prawo. Dlaczego trzeba było zrobić tak? Jest oczywiste, że największy dzielnik w tym przykładzie -6, dlatego też, aby po podzieleniu na niego z prawej strony została jednostka, należy «odłożyć» od 144 właśnie 6 (o tym, że po prawej stronie powinna być jednostka, mówi dostępność wolnego członka ó stałe, nie razy na nieznanej).
Podzielimy na sześć i otrzymamy kanonicznej równanie elipsoidy:
(x-1)2/2+(y+5)2/1+z2/3=1
W stosowanej wcześniej klasyfikacji powierzchni 2 około uważany jest przypadek, gdy w centrum formacji znajduje się w początku układu współrzędnych. W tym przykładzie jest on przesunięty.
Wierzymy, że każda klamra z nieznanymi – to nowa zmienna. Czyli: a=x-1, b=y+5, c=z. W nowych współrzędnych środek elipsoidy pokrywa się z punktem (0,0,0), a zatem a=b=c=0, skąd: x=1, y=-5, z=0. W początkowych współrzędnych centrum kształty leży w punkcie (1,-5,0).
Elipsoida będzie się układało się z dwóch części: pierwszej w płaszczyźnie XY i drugiego w płaszczyźnie XZ lub YZ – to nie ma znaczenia). Kursy, na które podzielone są zmienne, są w kanonicznym równania do kwadratu. Zatem w powyższym przykładzie lepiej byłoby podzielić na pierwiastek z dwóch, jednostkę i pierwiastek z trzech.
Mniejsza przednia pierwszej elipsy, równoległa do osi Y, równa się dwa. Duża oś równoległa do osi X – dwóch korzeni z dwóch. Mniejsza przednia drugiego elipsy, równoległa do osi Y, pozostaje ten sam – jest ona równa dwóm. A duża oś równoległa do osi Z, równa się dwóm korzeni z trzech.
Za pomocą pochodzących z pierwotnego równania przez konwersję do kanoniczną rodzaju danych możemy narysować elipsoida.
Podsumowując
Oświetlony w tym artykule temat jest dość obszerna, ale, w rzeczywistości, jak można teraz zobaczyć, nie jest bardzo skomplikowany. Jej opanowanie, w rzeczywistości kończy się na tym momencie, kiedy заучиваете nazwy i równania powierzchni (i, oczywiście, jak one wyglądają). W powyższym przykładzie możemy szczegółowo traktowali każdy krok, ale doprowadzenie równania do kanoniczną rodzaju wymaga minimalnej wiedzy w wyższej matematyce i nie powinno powodować żadnych trudności u ucznia.
Analiza przyszłości grafika istniejącej równości już trudniejsze zadanie. Ale dla jej pomyślnego rozwiązania wystarczy zrozumieć, jak są zbudowane odpowiednie krzywe stożkowe ó elipsy, paraboli i inne.
Przypadki degeneracja – jeszcze bardziej prosty temat. Z powodu braku niektórych zmiennych łatwiejsze i nie tylko obliczenia, jak już było powiedziane wcześniej, ale i samo budowanie.
Jak tylko można śmiało nazwać wszystkie rodzaje powierzchni, zmieniać stałe, przekształcając wykres w tę lub inną figurę ó tematem będzie opanować.
Sukcesów w nauce!
Article in other languages:
PT: https://tostpost.com/pt/educa-o/38928-a-superf-cie-da-ordem-de-2-exemplos.html
ZH: https://tostpost.com/zh/education/18836-surface-of-order-2-examples.html

Alin Trodden - autor artykułu, redaktor
"Cześć, jestem Alin Trodden. Piszę teksty, czytam książki, Szukam wrażeń. I nie jestem zły w opowiadaniu ci o tym. Zawsze chętnie biorę udział w ciekawych projektach."
Nowości
Rozgałęźników Rodion Romanowicz - biedny i sponiewierane student, główny bohater powieści "Zbrodnia i kara". Autorem dzieła jest Dostojewski Fiodor Michajłowicz. Dla psychologicznego przeciwwagi teorii Rodion Romanowicza pisarzem ...
Skąd powiedzenie "popa z uchwytem"?
W rosyjskiej mowy, istnieje wiele zabawnych trwałych wyrażeń, które są dobre i jak беззлобная żart, i jak dobroduszny naganę. Znamiennym przykładem - "popa z uchwytem". Skąd w ogóle wziął się tego języka? Co chce powiedzieć człowi...
Problemy ekologii ewolucyjnej teorii, популяционной biologii i innych nauk często dotyczą pojęcie zmienności (jako określonej i nieokreślonej). To kamień węgielny dla zrozumienia pochodzenia gatunków, ich zdolności do przystosowan...
Jak pisać wypracowania o sobie? Jak opowiedzieć o sobie prawda?
Często w szkołach zadają uczniom napisać pisma o sobie. Zadania te zwykle dają w liceum, bo w 16-17 lat uczniowie myślą całkiem świadomie i już mogą przedstawić swoje myśli na ten temat.Podstawowe pomysłPisma o sobie są popularną ...
Co to jest zginać kolan? Znaczenie słowa w różnych słownikach wyjaśnia około równie: leniuchować, wagary, wymigać od pracy. A oto względem występowania tego terminu językoznawcy dopóki nie zgodzili. Ktoś uważa, że słowo to pochodz...
"W rzeczywistości": przecinek gdzie umieścić? "W rzeczywistości" wyróżnia się przecinkami?
Jest takie obroty w języku polskim, o których nie można powiedzieć od razu, – to wstępne konstrukcji lub członkowie oferty, co oczywiście stwarza pewną trudność w postawieniu znaków interpunkcyjnych. Dziś za jeden taki przyp...



















Uwaga (0)
Ten artykuł nie ma komentarzy, bądź pierwszy!