Nedir teoremi ve teoremi bir kanıtı? Pisagor teoremi ispat

Sadece her öğrenci, ama her onurlu eğitimli kişi bilmeli ki, böyle bir teorem ve kanıtı teoremleri. Belki kavramları ve karşılamak için gerçek hayatta, ama yapısı pek çok bilginin yanı sıra, çıkarımlar yapmak, onlar kesinlikle yardımcı olacak. Bu yüzden biz ve düşünün bu makalede, yollar teoremleri kanıtlar, hem de aşina bir çok ünlü Pisagor teoremi.

Nedir teoremi

Eğer kabul lise matematik ders, çok sık onu karşılamak gibi bilimsel terimler gibi, teorem, aksiyom, tanım ve kanıt. İçin gezinmek programda okumak gerekir her biri, bu tanımları. Şimdi düşünün, böyle bir teorem ve kanıtı teoremleri.

Yani teoremi – bu tür bir iddia kanıt gerektirir. Düşünün bu kavram gerek paralel aksiyom gibi son kanıt gerektirmez. Tanımı zaten bir gerçek, bu yüzden hafife alınır.

Kapsam teoremleri

Yanlış düşünüyorum, bu teoremi uygulanır matematik. Aslında bu kadar değil. Örneğin, orada sadece inanılmaz sayıda teoremleri, fizik, izin, ayrıntılı olarak ve tüm tarafların dikkate bazı olgu ve kavramları. Buraya bağlanabilir teoremi Amper, Steiner ve diğer birçok. Kanıtlar gibi teoremleri izin iyi anlamak noktaları ataleti, statik, dinamik, ve diğer birçok kavramlar fizik.

Kullanım teoremleri matematik

Zor bir hayal bu, bilim, matematik gibi olmadan, teoremleri ve kanıt. Örneğin, kanıt teoremleri üçgenin izin ayrıntılı olarak incelemek için, bütün şekil özellikleri. Çünkü çok önemli anlamak belirtileri benzerlik özellikleri, ikizkenar üçgen ve birçok diğer şeyler.

Teoreminin Kanıtı meydanı için izin verir anlamak kolay hesaplamak için kare şekiller dayanarak bazı bilgiler. Çünkü, bilindiği gibi, çok sayıda formüller anlatan bulunabilir üçgenin alanı. Ama önce bunları kullanmak için çok önemli olduğunu kanıtlamak için mümkün ve rasyonel bir şekilde belirli bir durumda.

Nasıl ispat teoremi

Her öğrenci bilmeli ki, böyle bir teorem ve kanıtı teoremleri. Aslında kanıtlamak için herhangi bir onay o kadar kolay değil. Bunun için ameliyat birçok veri ve yapmak mümkün mantıksal çıkarımlar. Tabii ki, eğer iyi bir bilgi sahibi ve belirli bir bilimsel disiplin, bir teoremi kanıtlamak için zor olmayacaktır. En önemlisi, yordamı gerçekleştirmek için kanıt belirli bir mantıksal tutarlılık.

Daha:

Sinir impuls, onu dönüştürme ve aktarım mekanizması

Sinir sistemi savunan bir tür koordinatörü vücudumuzda. O komutları iletir beyin мускулатуре, organlara, dokulara ve işler sinyalleri gidiyor onlara. Tür olarak veri taşıyıcı tarafından kullanılan bir sinir dürtü. Neyi temsil ettiğini? Hangi hızda ça...

Isıl işlem çelik

Isıl işlem çelik yapılabilir çeşitli yolları vardır. Uzmanlar ayırt aşağıdaki seçenekleri sunar: 1. Ateş. 2. Normalleştirme. 3. Sertleşme olduğunu. 4. Tatil. Isıl işlem çelik kızartma temsil ısıtma ürün sıcaklık 840 900 derece. Sırasında belirtilen s...

Ana tür duyumlar: sınıflandırma, özellikleri

Psikoloji – bu çalışmalar bilim farklı zihinsel süreçler, olaylar ve durum. Bu bilgilendirici zihinsel süreçleri içerir hissi, görünüm, algı, hayal gücü, konuşma, düşünme, ezberleme, dinleme, kaydetme, vb. bu makalede, biz daha duralım böyle bi...

öğrenmek için bir teoremi kanıtlamak için bu bilimsel disiplinler gibi geometri ve cebir olması gerekir iyi bir bagaj, bilgi, bilmek de kendisi algoritması kanıtı. Ana eğer böyle bir prosedür, o zaman matematik problemlerini çözmek daha sonra sizin için zor olmayacaktır.

Hakkında bilinmesi gerekenler kanıtı teoremleri

Nedir teoremi ve teoremleri kanıtlar? Bu soru, bir sürü insan endişe günümüz toplumunda. Öğrenmek çok önemlidir kanıtlamak için matematiksel teoremi, bu size yardımcı olacaktır gelecekte inşa mantıksal ve gelmek, belirli bir sonuç.

O halde, ispat teoremi doğru yapmak çok önemli, doğru bir resim. O görüntüleyin bütün verileri, belirtilen koşulu. Ayrıca çok önemli tüm bilgileri kaydetmek, bir altında görev. Bu, size yardımcı doğru analiz etmek, görevi anlamak, tam olarak hangi değerler içinde verilmiştir. Ve sonra gibi işlemleri yürütmek geçebilirsiniz geçirmez. Bunun için mantıklı bir sıraya zinciri düşünceler kullanarak diğer teoremleri, aksiyomları veya belirlemek. Sonuç kanıt olması sonucu, gerçeği olduğu tartışılmazdır.

Ana yolları teoremleri kanıtlar,

Okul ders matematik iki yolu vardır teoremi kanıtlamak için. En sık görevleri kullanmak için doğrudan bir yöntem, hem de ispat yöntemi kötü. İlk durumda, sadece bir analiz mevcut veriler ve onlara güvenerek, yapmak соответственные sonuçlar. Ayrıca çok sık kullanılan bir yöntem kötü. Bu durumda, biz tam tersi bir iddia ve kanıtlamak, bu yanlıştır. Buna göre biz tam tersi bir sonuç ve diyoruz ki, bizim yargı yanlıştı, yani belirtilen sağlanan bilgilerin doğru olduğunu.

Aslında pek çok matematik problemleri olabilir çözmek için birkaç yol vardır. Örneğin, Fermat teoremi kanıt vardır. Tabii ki, bazı kabul edilir tek bir yolu var, ama, örneğin, Pisagor teoremi düşünebilirsiniz, hemen birkaç tanesi.

Nedir Pisagor teoremi

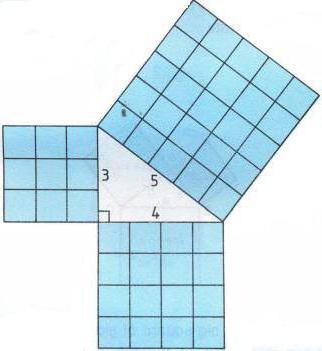
Tabii ki, her öğrenci bilir ki, Pisagor teoremi ile ilgilidir tam olarak dik üçgen. Ve sesler o kadar: «Kare hipotenüs karelerinin toplamına eşittir катетов». İsmine rağmen, bu teoremi, açık değildi kendisi Пифагором ve daha önce ona. Varbirkaç yolu bir kanıt bu iddiaları, ve biz bunlardan bazılarıdır.

Göre, bilimsel verilere göre, başlangıçta ele eşkenar dik üçgen. Daha sonra inşa kareler tüm yüze. Kare üzerine inşa гипотенузе, oluşacak dört eşit arasında bir üçgen. O zaman nasıl bir şekil inşa катетах, yalnızca oluşacaktır böyle iki üçgen. Böyle bir kanıt Pisagor teoremi için en kolay.

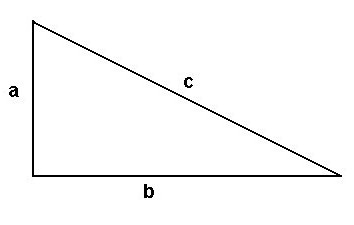
Düşünün bir başka kanıtı bu teoremi. Onu kullanmak için gereken bilgi değil, sadece geometri, aynı zamanda, cebir. Kanıtlamak için bu teoremi bu şekilde, yeniden inşa etmemiz gereken dört benzer dikdörtgen, üçgen, ve imzalamak, onların bir parçası gibi a, b ve c

Oluşturmak için bu üçgenler gerekir böylece sonuç olarak başardık iki kare. Açık biri olacak taraf (a+b), ve bu iç – s. bulmak İçin meydanı iç kare bulmalıyız eseri ile*s. Ve burada bir bulmak için kare büyük kare katlanabilir kare küçük kareler eklemek meydanı alınan dikdörtgen, üçgen. Şimdi, seçtiğiniz bazı cebirsel işlemler, almak için böyle bir formül:

Ve²+ve²=c²

Aslında, orada çok sayıda yöntem teoremleri kanıtlar. Dik, üçgen, kare veya diğer şekiller ve onların özellikleri düşünebilirsiniz kullanarak çeşitli teoremleri uygulama ve kanıt. Pisagor teoremi sadece bir zamanda, bir onay.

Yerine hapis

önemlidir formüle teoremi, hem de onları doğru kanıtlamak. Tabii ki, bu işlem oldukça zordur, bunu uygulamak için gerekli değil, sadece bilmek ve bir ameliyat, bir sürü bilgi, ama aynı zamanda mantıksal zinciri oluşturmak için. Matematik – bu çok ilginç bir bilim, bir sonu yok, kenar.

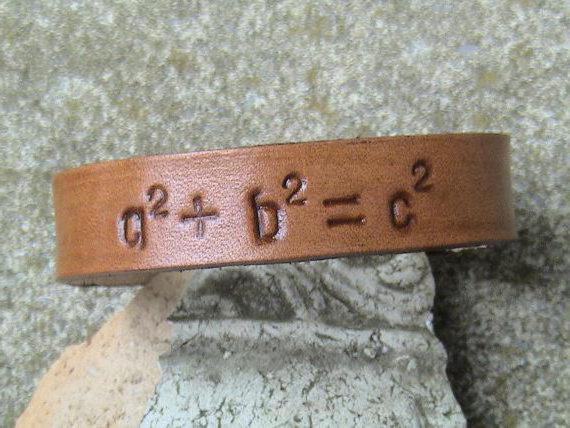
Başlayın, onu öğrenmek için, ve sadece düzeyini yükseltmek, onun zeka, ama almak çok sayıda ilginç bilgi. Takipteyim çok iyi bir eğitim zaten bugün. Anlayarak temel ilkeleri kanıt teoremleri, sen vakit geçirmek için büyük yarar.