鈍角:長さの面では、和の角度です。 に記載の鈍角三角形
も就学前の子どもたちに知ってもらうように三角形です。 それのみを理解しはじめている。に学校に通えるようになった。 ターが鈍角です。 かれは、最も簡単な方法を見れば写真の彼のイメージです。 理論的には、このいわゆる単純多角形"三面と頂点のある鈍角です。
について説明できる
幾何学と区別するこれらの種類の形状を三角、四角や三角鈍ます。 の性質を単純多角形と同じです。 ですから、全ての種類を観察する格差です。 の合計の長さの双方がよりの長さの三側となります。
 で確認することだいて完成した作品ではなく、個人の頂点には、チェックする必要があり遵守のための主要条件: の和角鈍角三角形等180Oです。 同様に他の種類の形状を三方をします。 しかし、鈍三角形の角にするとともに、今後さら90Oで、残りの二つが結合するものとします。 この角の長い側となります。 しかし、この全てではありませんの性質が鈍角です。 とものみこれらの特徴は、学生がさまざまな課題を解決するための幾何学します。
で確認することだいて完成した作品ではなく、個人の頂点には、チェックする必要があり遵守のための主要条件: の和角鈍角三角形等180Oです。 同様に他の種類の形状を三方をします。 しかし、鈍三角形の角にするとともに、今後さら90Oで、残りの二つが結合するものとします。 この角の長い側となります。 しかし、この全てではありませんの性質が鈍角です。 とものみこれらの特徴は、学生がさまざまな課題を解決するための幾何学します。
各ポリゴン三つの頂点でもtrueを推進していくことが当者まで角度そのサイズに等しい和のnonadjacent内部の頂点です。 の周囲の鈍三角の計算と同じようにその他の形状です。 和の長さがすべての側面です。 を決定する領域の三角形数学者由来し、種々の数式によっては、どのオリジナルデータです。
以上
人間の神経系としてのコーディネーターになります。 いろいろなものを発信コマンドからの脳の筋肉、臓器、組織、プロセスの信号が来ています。 どのようなデータの中の神経インパルス. 何ですか? スピードす。 これらの数に基づく総合的質疑応答えないことを示しています。う神経インパルス?という波の励起とスプレッドの繊維としての対応刺激の神経細胞となる。 このメカニズムが確実に情報伝達から各種受容体のきるようになりました。 そして、異なる臓器(筋肉や腺). どこのプロセスを表す生理はどうすればいいですか? ...
ピラミッドの中、この日は謎できます。 その謎のが一番いいと思います。 世界の存在を知りこれらのピラミッドです。 に20世紀絵画の奇跡でしたからとられます。 そして人類の知 このピラミッドが存在した。 今日でも、これらの宝物の世界の文化を厳重に保護されて政府はこの国です。ただし、ピラミッドの中国にとって大きな関心事項の多くの研究者と考古学者. 言い伝えでは、既存のがこの国のピラミッド、外国人の人が訪れています。 の正確な年齢のこれらの独自の構造を、誰もが知っています。 最初の情報について...
乱のDecembristsに1825–数のイベントに、我が国ることが知られているすべてます。 一般に、ウズベキスタンのほとんどの人が想像するこのイベントで何を終了しました。 多くの歴史学者に捧げてその活動の研究ではこの素晴らしい。すべてのDecembrist反乱が大きな影響を与えるのは、国家開発の一部のものが多いと感じている今日のイベントの結果何が起きたのか、元老院広場があります。[rek1]まず、その原因Decembrist乱. そして、もちろん、人を忘れて、戦争の18...
右概要
一の最も重要な条件の解決の問題を形状右図のようです。 多くの先生の数学であると考えられないこと"である可視化から与えられたもので、何が必要なのですが80%であり、正しい答えします。 そのため、お客様が所有する重要な知を構築する方法を鈍角です。 が必要な場合も想定図を描くことができずポリゴン三方ように角度を超90Oです。
 の場合は特定の値の長さの度の角度を鈍角が必要に従います。 が必要となく正確に描き、角度を計算している純に比例データで条件を指定して表示します。
の場合は特定の値の長さの度の角度を鈍角が必要に従います。 が必要となく正確に描き、角度を計算している純に比例データで条件を指定して表示します。
メインライン
この学生の知るだけでなく、データのみをどのように見える形にします。 できない閉じ込めに関する情報はどのく三角鈍、長方形です。 コース数学その知識の主な特徴の数値は完了です。
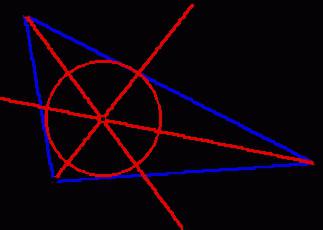 では、各学生は明確に定義bisectorsは、中央値は、内側に垂直および標高を示しています。 また、ニーズを知る主なプロパティを持ちます。
では、各学生は明確に定義bisectorsは、中央値は、内側に垂直および標高を示しています。 また、ニーズを知る主なプロパティを持ちます。
では、bisectors分の角度が半分になり、反対の方向に–セグメントになるに比例した隣接する面ます。
中央区分毎の三角形を二つに等しい。 時点においても交差し、それぞれに分かれて2セグメントの比率は2:1で見た場合、上からかかっていたのです。 大量の中央値は、常にその下側にします。
注意が払われます。 垂直反対側にコーナーです。 高度の鈍角によって特徴が異なります。 だから、頂点が入っているので、単純多角形、その続編です。
垂直bisector-セグメントからのセンターの端の三角形です。 しかし、それを直角にします。
サ
初の研究の幾何学、必要とする子ども理解の方法を描くのは鈍トライアングルを学ぶためのものと区別してその定義は、以下のウェブサイトを覚え、その基本的性質の研究に取り組んだ。 でも高校生のこの知識は不十分です。 例えば、試験を受けることがしばしについてのご質問に記載のと刻まれる。 最初に係るすべての頂点の角に、第二には共通点とすべての当事者ます。
の構築に刻まれた囲が鈍角でもより複雑にすることが必要なことから、始めにセンターのサークルやその半径です。 ちなみに必要なツール参加費無料、どなたでもご参加の場合だけでなペン、定規、コンパスです。
と同じ困難が構築に刻まれたポリゴンと出ています。 数学者由来し、種々の関数をその位置をできる限り正確になります。
刻まれた三角形にあたって
ことばのパスを通じてすべての頂点とすると、"で記述されています。 その主な特徴であるようになっていただけます。 どのように記述しなければならな円鈍角で、覚えておいてそのセンターでおすすめのperpendicularsを通じてその中間の側の図です。 場合に急性角ポリゴン三つの頂点は、この点内では、鈍–えます。
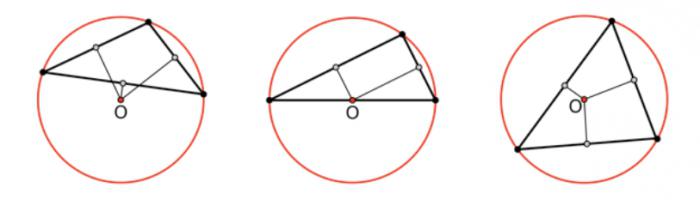
知ることは、例えば、一つの側面の鈍角三角形等、その半径を見つけることが可能で、角度の対応ものです。 その正弦波と同額となりますの結果から分割の長さの部分2R(R-あの円の半径)です。 この罪の角度以½ます。 その角度が150Oです。
ただける場合の半径の円囲が鈍角では、ますます便利に関する情報に面(c,v,b)とその地域S.では半径として計算(c×v×b):4x S.ように、何を使う:斜角鈍角isosceles、右の傾斜したりします。 のような状況下、式を処分する場合は、次の算式にすることができ、地域の指定されたポリゴンと三方をします。
を記述する三角形にあたって
も多いと刻まれる。 により算式に半径の数値を乗じた½の外周と同額となりますの地域は三角形です。 しかし、明らかに把握しておく必要があり、両側の鈍角です。 そのため½の周囲には、必要な方はその長さの割による2.
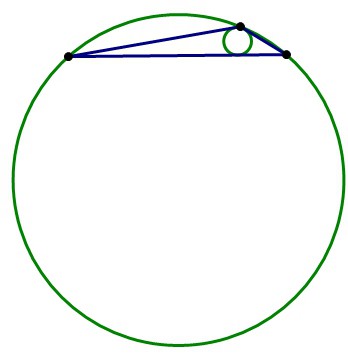
理解することはセンサーが登録され鈍トを開く三bisectorsます。 これらの線分の角度を半分にします。 そうで交差するセンサーです。 しかし、彼は数字から、それぞれます。
半径の円が刻まれた鈍角、equalsの平方根の商(p-c)x(p-v)×(p-b):p. がp–properiter三角形,c,v,b,–作します。
Article in other languages:

Alin Trodden - 記事の著者、編集者
"こんにちはっAlin踏. 私はテキストを書いたり、本を読んだり、印象を探したりしています。 そして、私はそれについてあなたに伝えることで悪くないです。 私はいつも面白いプロジェクトに参加することができて幸せです."
関連ニュース
もの学校コースの解剖学習慣を身につけられるよう単純な生物のパターンの構造生活の多細胞生物の基礎のすべての細胞です。 グループのことによって上昇する組織、臓器形します。 後者の組み合わせで、システムの重要な機能-代謝います。それでは、組織の構造と機能の研究から中等学校カリキュラムです。 考えるどんな種類の組織が人体組成物は、上皮様々なデータ構造としてどのような値です。[rek1]動物組織分類組織は、その構造と機能の特殊性の開発と機能にとって大切なの生活の全て...
メモリは精神的なプロセスからなる確保、保管、その後の再生の情報です。 これらの事業の保存のヒトでの経験です。研究の経緯最初の研究のメモリに始まった古代になって学習プロセスです。 古代ギリシャには、例えば、慣習することができるものとし、情報が入り込むことにより、人の頭部の特定の材料微粒子、即、ソフトマターの脳のように、粘土またはワックスします。[rek1]その後、著“油圧”モデルの神経システム、デカルトを策定し、その後に日常的に同じ神...
シリウス-インスティテュートは、惑星や星コンステレーション"か?
明天体がその場で地球からはシリウス-インスティテュート-ボーイが入り口に車をつ星蟹酢大きます。 そして二つ以上の倍以上の陽の光を輝かしい時代と比較した。 特別な商品の時点では地球を除き、極度北緯、シリウス-インスティテュートです。 地球や太陽光システムに位置すさから女8.6光年の約9兆円に達し、460億キロメートルとなります。 近くにはalpha Centauriます。 の温度をスターは9600度(太陽の下ではほとんどつながる可能性があり、五百します。[r...
と呼ばれるdeclensionのロシア語のか? Declensionの名詞
私たちの多くはまだ学校だという辞退届けします。 ものを再現すべてのニュアンスが関連付けられ、力になっています。 が知識のルールに関連するdeclensionの名詞、助けないスペルミスは、今後ます。辞退届...
科学の研究の社会的プロセスの二つに集団:人文社会です。 それぞれ使用方法やアプローチを研究します。 社会科学などの歴史学、経済学、政治学などです。 中の人文科学分野などの美術史学、文献学、心理学、エスノグラフィなどです。 理念のもつ、他のグループです。 社会科学研究科によって支配されている社会的方法を学習します。 彼の研究の接続、人と人との関係性を重視します。 人道的なアプローチの研究の特徴は、彼の心の背景、精神世界では、個人志向します。[rek1]社会生...
フランス最大の領域内に政府が西ヨーロッパに在住しています。 で株式の境界線八その他の国に–ドイツ、ベルギー、スイス、イタリア、スペイン、アンドラ、ルクセンブルク、モナコます。 このカント–最も美しい、魅力的な観光客ます。 は何か、そして地理的な特徴は、気候変動との積す。地理的位置にあたって外観のフランス領域ではほとんどを彷彿とさせる正六角形です。 彼女の最高の位置を指摘されたように、古代歴史学者とcartographersます。 例...



















コメント (0)
この記事にはコメントすることですが、最初の!