Verteilungsfunktion Zufallsvariable. Als eine Funktion der Verteilung der Zufallsvariable
Um eine Verteilungsfunktion der zufälligen Variablen und deren Variablen verwenden, sollten Sie alle Besonderheiten dieser Fachgebiete. Es gibt ein paar verschiedene Methoden für die Suche nach den betrachteten Werten, einschließlich der änderung der Variablen und die Erzeugung des Augenblicks. Verteilung - ein Konzept, in dessen Grundlage bilden die Elemente wie Dispersion, Variation. Aber Sie Kennzeichnen nur den Grad des Ausmaßes der Streuung.

Weitere wichtige Funktionen zufällige Werte sind diejenigen, die gebunden sind und sind unabhängig und identisch verteilt. Zum Beispiel, wenn X1 - Gewicht zufällig ausgewählten Individuum der population Männchen, X2 - Gewicht des anderen, ..., Xn - Gewicht einer weiteren Person aus der männlichen Bevölkerung, dann müssen Sie lernen, wie eine zufällige Funktion X verteilt. In diesem Fall gilt das klassische Theorem, genannt zentralen äußerste. Sie können zeigen, dass bei großen n die Funktion sollte Standard-Software-Distributionen.
Funktion einer Zufallsvariable
Zentrale Grenzwertsatz ist für die diskrete approximation der betrachteten Werte, wie Binomialverteilung und Poisson. Die Funktion der Verteilung von zufälligen Größen, behandelt in Erster Linie auf die einfachen Werte einer Variablen. Zum Beispiel, wenn X ist eine kontinuierliche zufälligen Wert, der einen eigenen Wahrscheinlichkeitsverteilung. In diesem Fall untersucht, wie eine Funktion der Dichte von Y, indem Sie zwei verschiedene Ansätze, nämlich die Methode zur Verteilung der Funktionen und ändern der Variablen. Zunächst beschreibt nur wechselseitig eindeutige Werte. Dann die Technik ändern müssen änderungen der Variablen, die Wahrscheinlichkeit Sie zu finden. Schließlich müssen Sie wissen, wie die inverse Funktion der Verteilungsfunktion verwendet kann helfen, Zufallszahlen zu simulieren, die Folgen von bestimmten aufeinander folgenden Schemas.
Mehr:
Das Deutsche Flugzeug "Messerschmitt-262": die Geschichte der Entstehung, Merkmale, Foto
High-Speed-Strahltriebwerk-Kämpfer-Abfangjäger Messerschmitt ME-262 Schwalbe („Messerschmitt ME-262 Schwalbe») erschien auf dem Schlachtfeld nur im Jahr 1944. Man kann nicht genau sagen, für welchen Job diese Maschine bestimmt. Experiment...
Moderne Schule: Geschichte, Voraussetzungen, Probleme. Modelle der modernen Schulen
Historische Entstehung von Schulen förderte den Wunsch der Menschen die Welt zu erkennen und erweitern Ihre Kenntnisse. Deshalb versucht der Mensch zur Gemeinschaft mit den weisen und sehnte sich danach von Ihnen zu lernen wissen.die Geschichte der m...
"Haare zu Berge": Bedeutung, Herkunft фразеологизма
In der Russischen Sprache treffen eine ausreichende Anzahl von geheimnisvollen Floskeln, über deren Bedeutung schwer zu erraten. Die sprachliche Konstruktion „die Haare» gehört eindeutig zu den solchen. Zum Glück, der Ursprung dieses Ausd...
Die Methodik der Verteilung der betrachteten Werte
Die Methode der Verteilungsfunktion die Wahrscheinlichkeitsverteilung der Zufallsvariable ist anwendbar, um zu finden Ihre Dichte. Bei der Verwendung dieses Verfahrens berechnet kumulative Wert. Dann, differenzieren, können Sie die Dichte der Wahrscheinlichkeit. Wenn Sie nun eine CUDA-Methode Verteilungsfunktion, kann man sich überlegen noch ein paar Beispiele. Lassen Sie X – kontinuierliche Zufallsvariable mit einer bestimmten Dichte der Wahrscheinlichkeit.
Was ist die Dichtefunktion der Wahrscheinlichkeit von x2? Wenn die Karte oder der graph der Funktion (oben und rechts) Y = X2, kann man bemerken, dass es mit steigendem X und 0 <y<1. Jetzt müssen Sie die betreffende Methode zu finden, Y., Zuerst wird die kumulative Verteilungsfunktion, differenzieren müssen nur um die Dichte der Wahrscheinlichkeit. Auf diese Weise erhalten wir: 0<y<1. Die Methode der Verteilung der erfolgreich umgesetzt wird, um eine Y, wenn Y ü zunehmende Funktion X. Übrigens, f (y) integriert 1 über y.
Im letzten Beispiel, die mit großer Sorgfalt für die Indizierung verwendeten kumulativen Funktionen und Dichte der Wahrscheinlichkeit entweder mit einem X oder Y, um anzugeben, zu welcher Zufallsvariable Sie gehörten. Zum Beispiel, wenn Sie sich eine kumulative Verteilungsfunktion Y haben X. Wenn Sie eine zufällige Größe X und seine Dichte, es muss nur differenzieren.
Die Technik der änderung der Variablen
Let X – kontinuierliche Zufallsvariable die Verteilungsfunktion angegeben als mit dem gemeinsamen Nenner von f (x). In diesem Fall, wenn Sie den Wert y in X = v (Y), so erhält man den Wert für x, z.B. v (y). Nun, brauchen eine kontinuierliche Verteilungsfunktion Zufallsvariable Y. wobei die erste und die zweite Gleichheit gilt der Ort der Bestimmung der kumulativen Y. die Dritte Gleichheit erfolgt, weil Teil der Funktionen, für die u (X) ≤ y, gilt auch, dass X ≤ v (Y). Und zuletzt wird für die Bestimmung der Wahrscheinlichkeit in einem kontinuierlichen zufälligen Größe X. Jetzt muss man die abgeleitete von FY (y), kumulative Verteilungsfunktion Y, um die Dichte der Wahrscheinlichkeit Y.
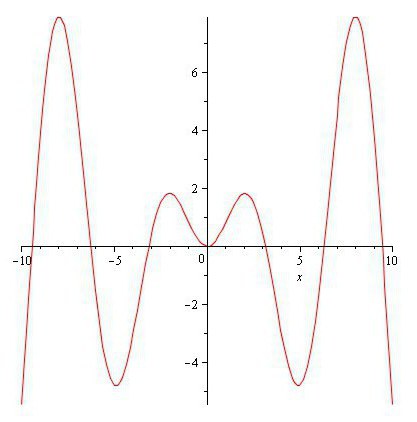
Verallgemeinerung für Funktionen reduzieren
Let X – eine kontinuierliche Zufallsvariable mit der gemeinsamen f (x), definiert über c1<x<c2. Und lassen Sie Y = u (X) – Abnehmender Funktion von X mit der inversen X = v (Y). Da die Funktion kontinuierlich ist und nachläßt, gibt es eine inverse Funktion X = v (Y).
Für die Lösung dieser Frage möglich, quantitative Daten zu sammeln und verwenden Sie die empirische kumulative Verteilungsfunktion. Mit diesen Informationen und unter Berufung auf Ihr, kombinieren müssen Proben der Mittel, Standardabweichungen, Medien und so weiter.
Ebenso auch eine ziemlich einfache probabilistische Modell kann eine große Anzahl von Ergebnissen. Zum Beispiel, wenn die Münze werfen 332 mal. Dann wird die Anzahl der Ergebnisse von coups mehr, als bei google (10100) – eine Zahl, aber nicht weniger als 100 Trillion mal höher als die der Elementarteilchen im bekannten Universum. Nicht interessant ist die Analyse, die eine Antwort auf jedes mögliche Ergebnis. Benötigen Sie mehr als ein einfaches Konzept, wie die Zahl der Köpfe oder die am längsten laufende Schwänze. Um sich auf Themen zu konzentrieren, von Interesse, nimmt sich ein bestimmtes Ergebnis. Die Definition in diesem Fall Folgendes: Zufallsvariable ist die reellen Funktion mit probabilistischen Platz.
Band S Zufallsvariable manchmal als Raum der Zustände. So, wenn X- überdachte Wert, also N = X2, exp ↵X, X2 + 1, tan2 X, bXc und so weiter. Der Letzte von Ihnen, rundet X auf die nächste ganze Zahl, nennt man die Funktion des Geschlechts.
Verteilungsfunktion
Sobald definiert das interessierende Funktion der Verteilung der Zufallsvariable x, die Frage wird in der Regel wie folgt: „Was sind die Chancen, dass X fällt in eine Teilmenge der Werte B?». Beispiel: B = {ungerade zahlen}, B = {1 mehr} oder B = {zwischen 2 und 7} angeben, um diese Ergebnisse, die einen X-Wert der Zufallsvariable, der Teilmenge von A. also im obigen Beispiel beschrieben werden die Ereignisse wie folgt.
{X ungerade}, {X 1} = {X> 1}, {X liegt zwischen 2 und 7} = {2 <X <7}, um die drei Optionen oben für eine Teilmenge B. Viele Eigenschaften von zufälligen Größen nicht verbunden mit einer bestimmten X. vielmehr davon abhängen, wie X verteilt seine Werte. Dies führt zu einer Definition, die lautet wie folgt: die Verteilungsfunktion Zufallsvariable x die kumulative und ermittelt die quantitativen Beobachtungen.
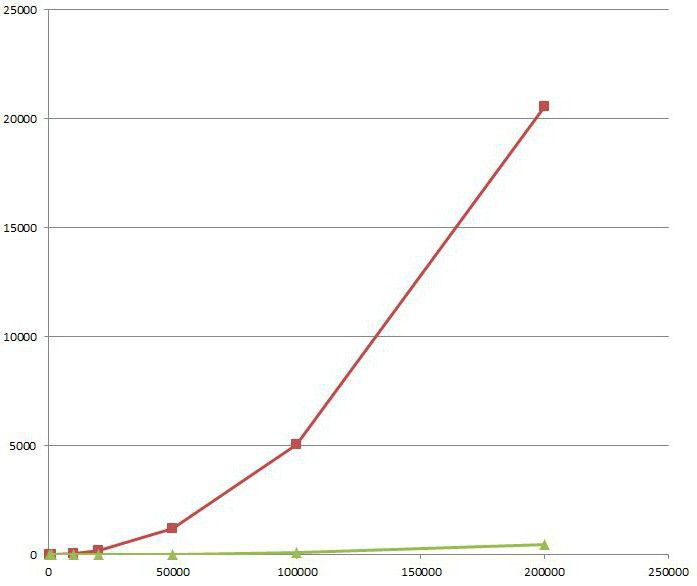
Zufällige Variable und Verteilungsfunktion
So können Sie die Wahrscheinlichkeit berechnen, dass die Verteilungsfunktion Zufallsvariable x nimmt Werte im Intervall durch Subtraktion. Sollte man über die Aufnahme oder den Ausschluss von Endpunkten.
Wir nennen eine zufällige Variable diskret, wenn es eine endliche oder zählbar unendlichen Raum der Zustände. So, X - Anzahl der Köpfe auf drei unabhängigen флипсах verschobenen Münzen, die steigt mit der Wahrscheinlichkeit p. Muss eine kumulative Verteilungsfunktion einer diskreten Zufallsvariable FX für X. sei X - Anzahl der Peaks in der Sammlung von drei Karten. Dann ist Y = X3 durch FX. FX beginnt mit 0, endet auf 1 und nicht abnimmt mit der Zunahme der x-Werte. Die kumulative Verteilungsfunktion FX einer diskreten Zufallsvariable X ist eine Konstante, mit Ausnahme von Sprüngen. Beim Sprung von FX ist stetig. Beweisen Sie die Aussage über die richtige Kontinuität der Verteilungsfunktion aus der Eigenschaft der Wahrscheinlichkeit ist es möglich mit Hilfe von Definitionen. Es klingt so: eine Konstante Zufallsvariable hat eine kumulative FX, die дифференцируема.
Um zu zeigen, wie dies geschehen kann, können Sie ein Beispiel nennen: ein Ziel mit einem einzigen Radius. Vermutlich. Dart gleichmäßig verteilt auf den jeweiligen Bereich. Für einiges λ> 0. Somit werden die Funktionen der kontinuierlichen Verteilung von zufälligen Größen stufenlos erhöht. FX hat die Eigenschaften einer Verteilungsfunktion.
Der Mann wartet auf den Bus an der Haltestelle, bis er eintrifft. Entscheiden Sie selbst, was aufgeben, wenn die Wartezeit 20 Minuten erreicht. Hier muss man eine kumulative Verteilungsfunktion für T. Zeit, als der Mensch noch wird auf dem Busbahnhof oder nicht Weggehen. Trotz der Tatsache, dass die kumulative Verteilungsfunktion bestimmt für jede Zufallsvariable. Immer noch Häufig verwendet werden andere Eigenschaften: Masse für die diskreten Variablen und die Dichtefunktion der Verteilung der Zufallsvariable. Normalerweise wird der durch eine dieser beiden Werte.
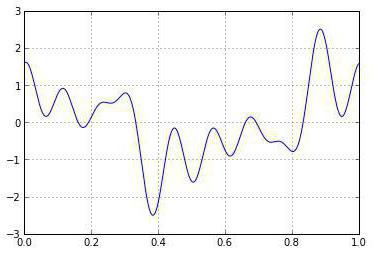
Massive
Diese Werte gelten die folgenden Eigenschaften, die eine Allgemeine (Massiv). Die erste beruht auf der Tatsache, dass Wahrscheinlichkeiten nicht negativ. Die zweite folgt aus der Beobachtung, dass der Satz für alle x=2S, Raum der Zustände für das X, bildet einen Gruppenwechsel wahrscheinlichen Freiheit X. Beispiel: Würfe einseitigen Münzen, deren Ergebnisse unabhängig voneinander sind. Sie können weiterhin bestimmte Aktionen durchführen, bis Sie Tore werfen. Lassen Sie das X kennzeichnet eine zufällige Größe, gibt die Anzahl der Schwänze vor dem ersten Kopf. Und p ist die Wahrscheinlichkeit in jeder gegebenen Aktion.
Also, die Masse ist eine Funktion der Wahrscheinlichkeit hat folgende charakteristische Merkmale. Da die Mitglieder bilden eine numerische Sequenz, X heißt geometrisch zufälligen Wert. Geometrische Schema c, cr, cr2,. , , , crn hat den Betrag. Und damit sn hat eine Grenze bei n 1. In diesem Fall ist die unendliche Summe ist die Grenze.
Die Masse oben bildet eine geometrische Abfolge mit Haltung. Daher natürlichen zahlen a und b. Die Differenz zwischen den Werten in der Verteilungsfunktion entspricht dem Wert des Bulk-Funktionen.
Die Betrachteten Werte Dichte eine Definition: X - Zufallsvariable, Verteilung der FX hat eine abgeleitete. FX, udovletvoryayuschaya Z xFX (x) = fX (t) dt-1, wird als Funktion der Dichte der Wahrscheinlichkeit. Und X heißt eine kontinuierliche random Wert. In der Haupt-Theorem Berechnung der Dichtefunktion ist die Ableitung der Verteilungsfunktion. Kann die Berechnung der Wahrscheinlichkeit durch die Berechnung bestimmter Integrale.
Da die Daten gesammelt und über mehrere Beobachtungen, dann sollte mehr als eine Zufallsvariable für die Zeit zu simulieren experimentellen Verfahren. Also, viele dieser Werte und Ihre gemeinsame Verteilung von zwei Variablen X1 und X2 bedeutet Ereignisanzeige. Für diskrete zufällige Größen definiert gemeinsame probabilistische massive Funktionen. Für kontinuierliche behandelt fX1, X2, wo die gemeinsame Dichte der Wahrscheinlichkeit erfüllt ist.
Unabhängige zufällige Variablen
Zwei zufällige Größen X1 und X2 sind unabhängig, wenn keine zwei damit verbundenen Veranstaltungen sind die gleichen. In Worten ist die Wahrscheinlichkeit, dass zwei Ereignisse {X1 2 B1} und {X2 2 B2} gleichzeitig auftreten,y ist gleich dem Produkt aus den oben genannten Variablen, dass jede von Ihnen ist individuell. Für unabhängige diskrete zufällige Größen eine gemeinsame probabilistische Bulk-Funktion, die ein Werk seitenhöchstzahlen Ionen. Für kontinuierliche zufällige Werte völlig unabhängig, die gemeinsame Dichtefunktion der Wahrscheinlichkeit - das Produkt der Werte der Cutoff-Dichte. Abschließend betrachtet n unabhängige Beobachtungen x1, x2,. , , , xn, die sich aus einer unbekannten Dichte oder Masse der Funktion f. Beispiel: der unbekannte Parameter in den Funktionen für exponentielle Zufallsvariable, die die Wartezeit des Busses.
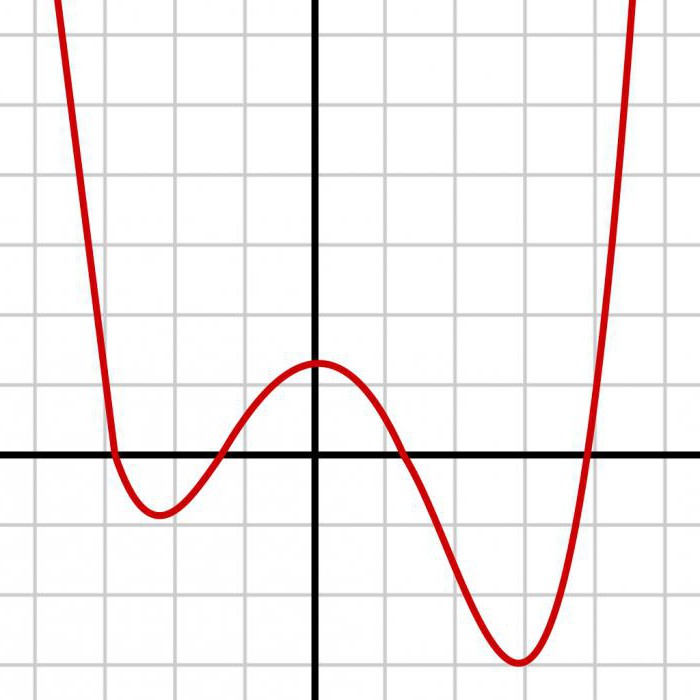
Simulation von zufälligen Variablen
Das Hauptziel dieser theoretischen Bereich – bieten Werkzeuge zum entwickeln умозаключительных Prozeduren, die auf fundierten Prinzipien der statistischen Wissenschaft. Also einer der ganz wichtigen Möglichkeiten der Anwendung der Software ist die Fähigkeit zur Erzeugung псевдоданные für die Simulation der tatsächlichen Informationen. Es gibt die Möglichkeit zu testen und zu verfeinern, die Methoden der Analyse vor der Notwendigkeit, den Einsatz in realen Datenbanken. Dies ist erforderlich, um die erforschten Eigenschaften der Daten durch die Simulation. Für viele Familien Häufig verwendete random variables R bietet Befehle, um Sie zu erstellen. Für andere Umstände benötigen Methoden der Modellierung einer Sequenz von unabhängigen zufälligen Größen, die eine gemeinsame Verteilung.
Diskrete zufällige Variable und Probe Command. Der Befehl sample verwendet für die Erstellung von einfachen und geschichteten Stichproben. Als Ergebnis, wenn Sie eine Sequenz von x, sample (x, 40) 40 wählt die Datensätze aus x so, dass alle Varianten der Größe 40 haben die gleiche Wahrscheinlichkeit. Es verwendet den Befehl R Standard für die Probenahme ohne Ersatz. Sie können auch für die Simulation von discrete random variables. Hierzu müssen Sie einen Raum der Zustände im Vektor x und Masse Funktion f. Die Herausforderung für replace = TRUE gibt an, dass das Sampling erfolgt mit dem Ersatz. Dann geben eine Probe von n unabhängigen zufälligen Variablen, die eine gemeinsame Masse Funktion f, wird eine Probe (x, n, replace = TRUE, prob = f).
Definiert, dass 1 ist der kleinste Wert dargestellt und 4 ist die größte von allen. Wenn der Befehl prob = f weggelassen, wird eine Probe wird gleichmäßig wählen der Werte im Vektor x. Überprüfen Simulation gegen Massen-Funktionen, die Daten erzeugen, können Sie die Aufmerksamkeit auf die Zeichen des doppelten Gleichheitszeichen, ==. Und nachgerechnet Beobachtungen, die nehmen jeden möglichen Wert für x. Sie können eine Tabelle machen. Wiederholen Sie dies für 1000 und vergleichen Sie die Simulation mit der entsprechenden Funktion der Masse.
Transformation Illustrieren Wahrscheinlichkeit
Zuerst simulieren homogene Verteilungsfunktion der zufälligen Variablen u1, u2,. , , , un auf dem Intervall [0, 1]. Etwa 10 % der zahlen sollte im Bereich [0,3, 0,4]. Dies entspricht 10 % der Simulationen auf dem Intervall [0,28, 0,38] für eine Zufallsvariable mit der gezeigten die Verteilungsfunktion FX. Ebenso etwa 10 % Zufallszahlen muss im Intervall [0,7, 0,8]. Dies entspricht 10 % der Simulationen auf dem Intervall [0,96, 1,51] Zufallsvariable mit der die Verteilungsfunktion FX. Diese Werte auf der x-Achse kann erhalten werden aus der Entnahme der Rückseite von FX. Wenn X eine kontinuierliche Zufallsvariable mit Dichte fX, positive überall in Ihrem Bereich, dann ist die Verteilungsfunktion streng erhöht. In diesem Fall ist die inverse Funktion FX FX-1, die als Funktion квантиля. FX (x) u nur dann, wenn x FX-1 (u). Konvertierung der Wahrscheinlichkeit folgt aus der Analyse der Zufallsvariable U = FX (X).
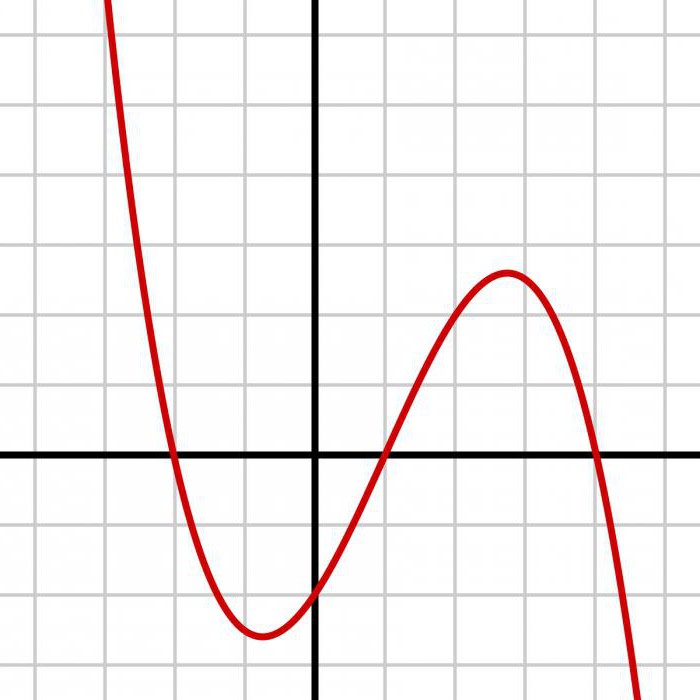
FX hat einen Bereich von 0 bis 1. Er kann keine Werte unter 0 oder über 1. Für Werte von u zwischen 0 und 1. Wenn man U simulieren, simulieren, ist es notwendig, eine zufällige Größe mit der Verteilung FX durch die Funktion квантиля. Nehmen Sie die Ableitung, um zu sehen, dass die Dichte von u variiert 1. Da die Zufallsvariable U besitzt eine Konstante Dichte im Intervall seine mögliche Werte, es heißt Uniform auf dem Intervall [0, 1]. Er simulierte in R mit dem Befehl runif. Identität heißt probabilistischen Transformation. Zu sehen, wie es funktioniert in dem Beispiel mit дротильной Brett. X zwischen 0 und 1, die Verteilung von u = FX (x) = x2, und damit die Funktion квантиля x = FX-1 (u). Sie modellieren unabhängige überwachung des Abstandes von der Mitte der Platten Dart, und die Schaffung eines einheitliche Zufallswerte U1, U2,. , , Un. Verteilungsfunktion und empirische basieren auf 100 Simulationen Verteilung der Dartscheibe. Für exponentielle Zufallsvariable, vermutlich u = FX (x) = 1 - exp (- x), und damit x = - 1 ln (1 - u). Manchmal ist die Logik besteht aus äquivalenten Aussagen. In diesem Fall verschmelzen die beiden Teile des Arguments. Die Identität mit der überquerung gilt für alle 2 {S i} S, anstelle von einiger Bedeutung. Die Vereinigung der Ci gleich dem Raum der Zustände S und jedes paar gegenseitig ausgeschlossen. Da Bi - gliedert sich in die drei Axiome. Jede Validierung basiert auf einer entsprechenden Wahrscheinlichkeit P. Für eine beliebige Teilmenge. Verwendung der Identität, um sicherzustellen, dass die Antwort nicht hängt davon ab, ob die Endpunkte des Intervalls.
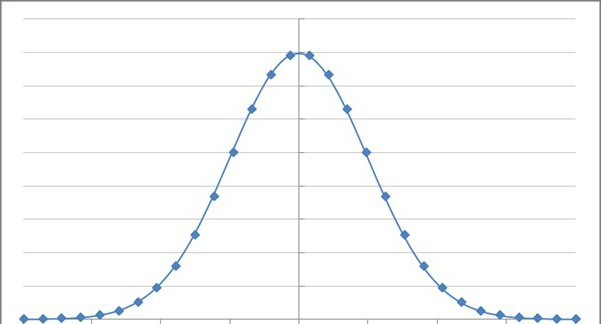
Exponentialfunktion und Ihre Variablen
Für jedenErgebnis in allen Ereignissen letztlich wird die zweite Eigenschaft der Kontinuität der Wahrscheinlichkeiten, die als аксиоматическим. Das Gesetz der Verteilung der Funktionen Zufallsvariable hier zeigt, dass jeder seine Entscheidung und Antwort.
Article in other languages:

Alin Trodden - autor des Artikels, Herausgeber
"Hi, ich bin Alin Trodden. Ich schreibe Texte, lese Bücher und suche nach Eindrücken. Und ich bin nicht schlecht darin, dir davon zu erzählen. Ich freue mich immer, an interessanten Projekten teilzunehmen."
Verwandte News
Wie richtig übersetzen Kilowatt in Pferdestärken
eine Solche Maßnahme, wie die Pferdestärke, wird in unserem Land für die Bestimmung der Leistung seit langem, immer vertrauter und verständlicher. Aber immer mehr Staaten, darunter auch Russland sich weigern, seine offizielle Anwe...
Was zu tun im Urlaub: die besten Ideen
die Schule und der Unterricht sind vorbei – kam die lang ersehnte Pause in der unendlichen Reihe Schultage und Hausaufgaben. Oft Jungs vorab viel darüber nachdenken, was zu tun ist im Urlaub. Vielleicht jemand plant, ein Aus...
Geschichte Кесем Sultan - brillante Leben der Frauen glänzend
die Geschichte Кесем Sultan überraschend kombiniert dichten historischen Gewebe mit feiner Patina von der Fiktion. Historiker, Studium der Sitten und der Chronik des osmanischen Reiches, unterschiedliche Meinungen über seinen Einf...
Am Anfang des 20 Jahrhunderts in Russland hauptsächlich landwirtschaftlich Stand die Frage. Während der Zarismus bediente Wirtschaftspolitik, die darauf abzielt, war überwiegend auf die Aufrechterhaltung des adeligen Grundbesitzes...
ein Ökosystem wird als eine Besondere Einheit von Pflanzen, Mikroorganismen und Tiere, in dessen Rahmen zwischen Ihnen ist ein Austausch von verschiedenen Stoffen und Energie. Jedes ökosystem hat einen charakteristischen nur für I...
Der Dänische Physiker Niels Bohr: Biografie, Entdeckung
Niels Bohr – der Dänische Physiker und Staatsmann, einer der Begründer der Physik in seiner heutigen Form. War der Gründer und Leiter des Kopenhagener Instituts für theoretische Physik, der Schöpfer der weltweiten wissenscha...





















Kommentare (0)
Dieser Artikel wurde noch kein Kommentar abgegeben, sei der erste!