Funkcje dystrybucji losowej wartości. Jak znaleźć funkcję rozkładu losowa
Aby znaleźć funkcje dystrybucji losowych i ich zmiennych, należy zbadać wszystkie cechy danej dziedziny wiedzy. Istnieje kilka różnych metod w celu znalezienia omawianych wartości, w tym zmiana zmiennej i generowanie momentu. Rozkład - takie pojęcie, u podstaw którego legły takie elementy, jak wariancja, wariacje. Jednak są one charakteryzują tylko stopień rozmachu rozpraszania.

Bardziej ważnych funkcji losowych są te, które odnoszą się i są niezależne od siebie, i tak samo rozmieszczone. Na przykład, jeśli X1 - waga losowo wybranego osobnika z populacji samców, X2 - waga innego, ..., Xn - waga jeszcze jednej osoby z męskiej populacji, to należy dowiedzieć się, jak funkcja losowa X jest rozprowadzany. W tym przypadku stosuje się klasyczne twierdzenie, zwana środkowej granicznej. To pozwala, aby pokazać, że przy dużych n funkcja należy standardowym распределениям.
Funkcji jednej zmiennej losowej
Centralnego twierdzenia granicznego jest przeznaczony do zbliżenia dyskretnych omawianych wartości, takich jak rozkład dwumianowy i Poissona. Funkcje dystrybucji losowych, rozpatrywane są w pierwszej kolejności na prostych wartości jednej zmiennej. Na przykład, jeśli X jest ciągła losowej wielkością, która ma własny rozkład prawdopodobieństwa. W tym przypadku bada się, jak znaleźć funkcję gęstości Y, stosując dwa różne podejścia, a mianowicie metoda funkcji rozkładu i zmian zmiennej. Najpierw rozpatrywane są tylko wzajemnie jednoznacznych wartości. Następnie należy zmodyfikować technikę zmiany zmiennej, aby znaleźć jej prawdopodobieństwo. Wreszcie, trzeba dowiedzieć się, jak odwrotna funkcja skumulowanego rozkładu może pomóc modelować liczby losowe, które podążają za pewnymi kolejnymi schematami.
Bardziej:
Główne etapy rozwoju psychiki w филогенезе
Rozwój psychiki w филогенезе charakteryzuje się kilkoma etapami. Rozważmy dwie główne historie związane z tym procesem.Филогенез - to historyczny rozwój, obejmującego miliony lat ewolucji, historię rozwoju różnych gatunków organizmów żywych.Ontogenez...
Co to jest gronkowiec i metody jego leczenia
Wielu w swoim życiu miał do czynienia z zakażeniem gronkowca. Dlatego konieczne jest posiadanie pełnej informacji o tej chorobie, aby w pełni zrozumieć, co dzieje się w organizmie. Więc co to jest gronkowiec? To bakterie, lub jedną z ich odmian, z kt...
Przed podjęciem się, że studiuje morfologia, należy zauważyć, że sam studiuje ten dział gramatyki. Tak, morfologia studiuje słowo jako część mowy, a także sposoby jego edukacji, jego formy, struktury i gramatyki wartości, a także poszczególne j...
Metoda dystrybucji omawianych wartości
Metoda funkcji rozkładu prawdopodobieństwa przypadkowej wartości odnosi się do tego, aby znaleźć jej gęstość. W przypadku tej metody jest obliczana kumulatywna wartość. Następnie, różnicowanie go, można uzyskać gęstość prawdopodobieństwa. Teraz, w przypadku metody funkcji rozkładu, można wziąć pod uwagę jeszcze kilka przykładów. Niech X ó ciągły losowa wartość z określonej gęstości prawdopodobieństwa.
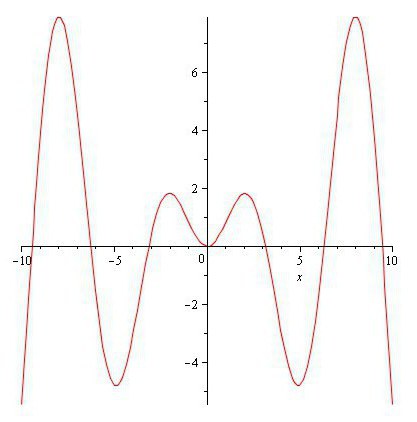
Jaka jest funkcja gęstości prawdopodobieństwa od x2? Jeśli spojrzeć lub narysuj wykres funkcji (na górze i po prawej) u = x2, można zauważyć, że jest ona coraz większej X i 0 <y<1. Teraz należy stosować takie metody, aby znaleźć Y. Najpierw jest skumulowana funkcja rozkładu, po prostu trzeba odróżnić aby uzyskać gęstość prawdopodobieństwa. Postępując w ten sposób, otrzymujemy: 0<y<1. Metoda dystrybucji z powodzeniem realizowany, aby znaleźć Y, gdy Y ó rosnąca funkcja X. przy Okazji, f (y) integruje się w 1 nad y.
W ostatnim przykładzie dużą ostrożność używane do indeksowania kumulacji funkcji gęstości prawdopodobieństwa lub za pomocą X, albo Y, aby określić, do jakiej zmiennej losowej należały. Na przykład, natomiast skumulowana funkcja rozkładu Y otrzymałeś X. Jeśli chcesz znaleźć zmienną losową X i jej gęstość, to ją po prostu trzeba odróżnić.
Technika zmiany zmiennych
Niech X ó ciągły losowa wartość zadana funkcji rozkładu z wspólnym mianownikiem f (x). W tym przypadku, jeśli umieścić wartość y w X = v (Y), to wartość x, np. v (y). Teraz trzeba uzyskać funkcję rozkładu ciągłego losowej wartości Y. Gdzie pierwsze i drugie równość ma miejsce z definicji skumulowana Y. Trzecia równość odbywa się dlatego, że część funkcji, dla której u (X) ≤ y, jest również prawdą, że X ≤ v (Y). I ostatnia jest wykonywane w celu określenia prawdopodobieństwa w ciągłej losowej wielkości X. Teraz trzeba wziąć pochodną od FY (y), skumulowana funkcja rozkładu Y, aby uzyskać gęstość prawdopodobieństwa Y.
Uogólnienie dla funkcji redukcji
Niech X ó ciągły losowa wartość z ogólnej f (x), określona nad c1<x<c2. I niech Y = u (X) – malejąca funkcja od X z odwrotnej X = v (Y). Ponieważ funkcja ciągłe i ubywa, istnieje funkcja odwrotna X = v (Y).
W Celu rozwiązania tego problemu można zbierać dane ilościowe i używać lek na kumulatywną funkcję rozkładu. Dzięki tej informacji i odwołując się nimi, trzeba kombinować próbki środków, odchylenia standardowe, multimedia i tak dalej.
Podobnie nawet dość prosta вероятностная model może mieć ogromną ilość wyników. Na przykład, jeśli odwrócić monetę 332 razy. Wtedy liczba otrzymanych wyników od przewrotów więcej, niż google (10100) – liczba, ale nie mniej niż 100 квинтиллионов razy wyższa cząstek elementarnych w znanym wszechświecie. Nie ciekawa analiza, która daje odpowiedź na każdy możliwy wynik. Konieczne jest bardziej prosta koncepcja, takie jak ilość głowic lub najdłuższy bieg ogonów. Aby skupić się na sprawach, będących przedmiotem zainteresowania, przyjmuje się określony wynik. Definicja w tym przypadku następujący: losowa wartość materialnej jest funkcją z вероятностным przestrzeni.
Zakres S losowa czasami nazywany przestrzenią stanów. Tak więc, jeśli X- dana wartość, to tak N = X2, exp ↵X, X2 + 1, tan2 X, bXc i tak dalej. Ostatnia z nich, zaokrągla X do najbliższej liczby całkowitej, nazywa się funkcją podłogi.
Opcje dystrybucji
Jak tylko określona potrzebne funkcja rozkładu losowa x, pytanie zazwyczaj staje się następująco: «Jakie są szanse, że X wpada w jakiś podzbiór wartości B?». Na przykład, B = {nieparzyste}, B = {1} lub B = {między 2 i 7}, aby określić te wyniki, które mają X, wartość losowa, w domenie A. w Ten sposób, w powyższym przykładzie można opisać wydarzenia w następujący sposób.
{X - nieparzysta liczba}, {X, 1} = {X> 1}, {X znajduje się między 2 a 7} = {2 <X <7}, aby spełniać trzy opcje powyżej dla części B. Wiele właściwości losowych nie są ze sobą powiązane z konkretnym X. Są raczej zależy od tego, jak X dystrybuuje swoje wartości. To prowadzi do definicji, która brzmi następująco: funkcja rozkładu losowa x kumulatywny i zależy ilościowymi spostrzeżeniami.
Losowe zmienne i funkcje dystrybucji
W Ten sposób można obliczyć prawdopodobieństwo tego, że funkcja rozkładu losowa x przyjmuje wartości w przedziale poprzez odjęcie. Należy pomyśleć o włączeniu lub wykluczeniu punktów końcowych.
Będziemy nazywać zmienną losową dyskretną, jeśli ona ma skończoną lub tablica nieskończona przestrzeń stanów. W ten sposób X - liczba głowic na trzech niezależnych флипсах przesuniętym monety, która wznosi się z prawdopodobieństwem p. Trzeba znaleźć kumulatywną funkcję rozkładu dyskretna losowa FX dla X. Niech X - liczba wierzchołków w kolekcji z trzech kart. To Y = X3 przez FX. FX zaczyna się od 0, kończy się na 1 i nie zmniejsza się wraz ze wzrostem wartości x. Kumulatywny FX funkcja rozkładu dyskretna losowa X jest stały, za wyjątkiem skoków. Podczas ucieczki FX jest ciągła. Udowodnić twierdzenie o prawidłowej ciągłości funkcji rozkładu z właściwości prawdopodobieństwa można za pomocą definicji. Brzmi ono tak: stała losowa wartość ma kumulatywną FX, która дифференцируема.
Aby pokazać, jak to może się zdarzyć, można przytoczyć przykład: cel z pojedynczym promieniem. Przypuszczalnie. dart równomiernie na określonym obszarze. Dla pewnego λ> 0. W ten sposób funkcji rozkładu ciągłych losowych płynnie wzrasta. FX ma właściwości funkcji rozkładu.
Człowiek czeka na autobus na przystanku, dopóki tego nie przybędzie. Decydując się na dla siebie, że zrezygnuje, gdy czekam osiągnie 20 minut. Tutaj trzeba znaleźć kumulatywną funkcji rozkładu dla T. Czas, kiedy człowiek jeszcze będzie znajdować się na dworcu autobusowym lub nie odejdzie. Mimo, że skumulowana funkcja rozkładu określona dla każdej losowej wartości. Nadal dość często będą wykorzystywane inne cechy: masa dla dyskretna zmienna i funkcja gęstości rozkładu losowej wartości. Zwykle pojawia się wartość przez jedną z tych dwóch wartości.
Masowe funkcje
Te wartości są traktowane następujące właściwości, które mają wspólny (masowy charakter). Pierwszy opiera się na tym, że prawdopodobieństwo nie jest negatywne. Drugie wynika z obserwacji, że zestaw dla wszystkich x=2S, przestrzeń stanów X, tworzy podział вероятностной wolności X. Przykład: rzuty необъективной monety, których wyniki są niezależne od siebie. Można nadal wykonywać pewne czynności, dopóki nie uda się rzut goli. Niech X oznacza zmienną losową, która daje liczbę ogonów przed pierwszą głową. A p oznacza prawdopodobieństwo, że w danym działaniu.
Tak Więc, masowa funkcja prawdopodobieństwa ma następujące cechy charakterystyczne. Ponieważ członkowie tworzą численную sekwencja, X nazywa geometrycznej losowej wielkości. Geometryczny schemat c, cr, cr2,. , , , crn ma sumę. I dlatego sn ma granicę przy n 1. W tym przypadku nieskończona suma jest limit.
Funkcja masy powyżej tworzy ciąg geometryczny z postawy. Zatem liczb naturalnych a i b. Różnica wartości funkcji rozkładu jest równa wartości masowego funkcji.
Rozważających wartości gęstości mają definicja: X - losowa wielkość, rozkład FX której ma pochodną. FX, która Z xFX (x) = fX (t) dt-1 nazywamy funkcją gęstości prawdopodobieństwa. A X nazywa ciągłej losowej wielkości. Do podstawowego twierdzenia rachunku całkowego funkcji gęstości jest pochodną dystrybucji. Można obliczyć prawdopodobieństwa poprzez obliczenie całki.
Ponieważ zbierają dane z wielu obserwacji wynika, że to powinno być traktowane więcej niż jednej losowej wartości na raz, aby modelować eksperymentalne procedury. W konsekwencji, wiele z tych wartości, a ich łączna alokacja dla dwóch zmiennych X1 i X2 oznacza podgląd zdarzeń. Dla dyskretnych losowych wartości określane są wspólne prawdopodobieństwa masowe funkcji. Dla ciągłych są traktowane fX1, X2, gdzie łączna gęstość prawdopodobieństwa jest zadowolony.
Niezależne zmienne losowe
Dwie losowe wartości X1 i X2 są niezależne, jeśli dowolne dwa związanych z nimi wydarzenia takie same. W słowach prawdopodobieństwo tego, że dwa zdarzenia {X1 2 B1} i {X2 2 B2} występują jednocześnie,y równa iloczynowi zmiennych wymienionych powyżej, że każda z nich odbywa się indywidualnie. Dla niezależnych dyskretnych losowych jest wspólna вероятностная masowa funkcja, która jest dziełem limitu ilości jonów. Dla ciągłych losowych będących niezależnymi, łączna funkcja gęstości prawdopodobieństwa - iloczyn wartości granicznej gęstości. Na zakończenie omówiono n niezależnych obserwacji x1, x2,. , , , xn, wynikające z nieznanej gęstości lub masowego funkcji f. Na przykład, nieznany parametr w funkcji wykładniczej dla losowej wielkości opisujące czas oczekiwania na autobus.
Symulacja zmiennych losowych
Głównym celem tej teoretycznej obszar ó zapewnić narzędzia niezbędne do rozwoju умозаключительных procedur opartych na uzasadnionych podstawach statystycznej nauki. Tak więc, jednym z bardzo ważnych zastosowań oprogramowania jest zdolność do generowania псевдоданные symulować rzeczywisty informacji. To daje możliwość testować i doskonalić metody analizy przed koniecznością wykorzystania ich w rzeczywistych bazach. Jest to konieczne do tego, aby zbadać właściwości danych za pomocą symulacji. Dla wielu często używanych rodzin losowych R zawiera polecenia do ich tworzenia. Dla innych okoliczności potrzebne metody modelowania sekwencji niezależnych losowych, które mają łączny rozkład.
Dyskretne zmienne losowe i wzorzec Command. Zespół sample służy do tworzenia prostych i uwarstwionych losowych próbek. W rezultacie, jeśli wprowadza sekwencję x, sample (x, 40) wybiera 40 rekordów z x w taki sposób, że wszystkie opcje rozmiaru 40 mają równe szanse. To wykorzystuje polecenie R domyślne dla próbki bez wymiany. Można używać również do modelowania dyskretnych losowych. Aby to zrobić, należy zapewnić przestrzeń stanów w wektorze x i masowej funkcji f. Wyzwanie dla replace = TRUE wskazuje, że сэмплирование dzieje się z wymianą. Następnie, aby dać próbkę z n niezależnych losowych, mających wspólną masową funkcji f, stosowany wzorzec (x, n, replace = TRUE, prob = f).
Ustalono, że 1 jest najmniejszą przedstawiających wartości, a 4 jest największym ze wszystkich. Jeśli zespół prob = f opuszczona, to próbka będzie wybierać równomiernie z wartości w wektorze x. Sprawdź symulację przeciwko masowej funkcji, która генерировала dane, można zwracając uwagę na znak podwójnego równości ==. I пересчитав obserwacji, które biorą każdą możliwą wartość dla x. Można zrobić tabelę. Powtórz to dla 1000 i porównać modelowanie z odpowiednią funkcją masy.
Ilustrowanie transformacji prawdopodobieństwa
Najpierw wymodelować jednorodne funkcje dystrybucji losowych u1, u2,. , , , un na przedziale [0, 1]. Około 10 % liczb musi mieścić się w zakresie [0,3, 0,4]. Odpowiada to 10 % symulacji na przedziale [0,28, 0,38] losowej wartości z przedstawionej funkcji rozkładu FX. Dokładnie tak samo około 10 % liczb losowych musi znajdować się w przedziale [0,7, 0,8]. Odpowiada to 10 % symulacji na przedziale [0,96, 1,51] losowej wartości z funkcji rozkładu FX. Te wartości na x oś może być uzyskane z pobierania zwrotnego od FX. Jeśli X - ciągłe losowa wartość o gęstości fX, pozytywnej wszędzie w swojej dziedzinie, to funkcja rozkładu ściśle wzrasta. W tym przypadku FX ma odwrotną funkcję FX-1, znany jako funkcja квантиля. FX (x) u tylko wtedy, gdy x FX-1 (u). Konwersja prawdopodobieństwa wynika z analizy zmiennej losowej U = FX (X).
FX ma zakres od 0 do 1. On nie może przyjmować wartości poniżej 0 lub powyżej 1. Dla wartości u między 0 i 1. Jeśli można modelować U, to należy naśladować zmienną losową z rozkładu FX poprzez funkcję квантиля. Wziąć pochodną, aby zobaczyć, że gęstość u waha się w granicach 1. Ponieważ losowa wartość U ma stałą gęstość w zakres swoich możliwości, to się nazywa równomiernego na przedziale [0, 1]. Jest on wzorowany na R za pomocą polecenia runif. Tożsamość nazywa вероятностным transformacją. Widać, jak to działa w przykładzie z дротильной deską. X między 0 i 1, funkcja rozkład u = FX (x) = x2, i, w konsekwencji, funkcja квантиля x = FX-1 (u). Można modelować niezależnych obserwacji odległości od centrum panelu dart, i tworząc przy tym jednolite losowe wartości U1, U2,. , , Un. Funkcja dystrybucji i empiryczne oparte są na 100 симуляциях dystrybucji rzutki-deski. Dla wykładniczej losowa, prawdopodobnie u = FX (x) = 1 - exp (- x), a zatem x = - 1 ln (1 - u). Czasami logika składa się z równoważnych zarzutów. W tym przypadku należy połączyć dwie części argumentu. Tożsamość z przekraczaniem podobnie dla wszystkich 2 {S i i} S, zamiast pewnej wartości. Stowarzyszenie Ci jedno przestrzeni stanów S i każda para wzajemnie wykluczona. Ponieważ Bi - podzielona jest na trzy aksjomaty. Każda kontrola opiera się na odpowiedniej prawdopodobieństwa P. Dla każdego podzbioru. Wykorzystując tożsamość, aby upewnić się, że odpowiedź nie zależy od tego, czy są włączone punkty końcowe okrążenia.
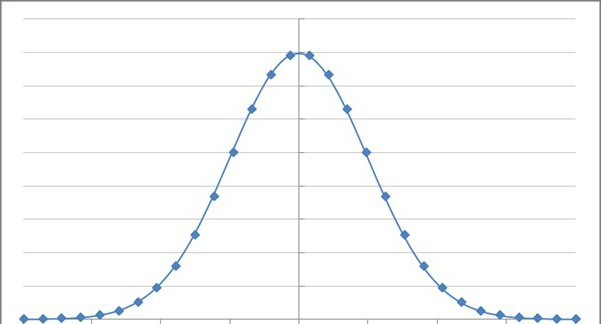
Funkcja Wykładnicza i jej zmienne
Dla każdegowyniki we wszystkich wydarzeniach, w końcu służy druga właściwość ciągłości prawdopodobieństwa, który jest uważany za аксиоматическим. Prawo podziału funkcji losowej wielkości tutaj pokazuje, że każdą swoją decyzję i odpowiedź.
Article in other languages:

Alin Trodden - autor artykułu, redaktor
"Cześć, jestem Alin Trodden. Piszę teksty, czytam książki, Szukam wrażeń. I nie jestem zły w opowiadaniu ci o tym. Zawsze chętnie biorę udział w ciekawych projektach."
Nowości
Jak poprawnie przetłumaczyć kws w mocy
Taki środek, jak końska siła, używane w naszym kraju do określenia mocy od dawna, stając się znanym i zrozumiałym. Jednak coraz więcej państw, w tym Rosja, rezygnują z jej oficjalnej aplikacji. Jednej miarą mocy, mającej wspólny o...
Radziecki propagandowy plakat jako narzędzie propagandy w różnych epokach
Nowoczesne PR-technologii daleko do przodu w porównaniu z środkami propagandowymi stosunkowo niedawna. Dziś na świadomość społeczna wpływają w największym stopniu media elektroniczne, wśród których kluczowe znaczenie w coraz więks...
Buriacji state university: wydziały, specjalności i opinie studentów
Przy wyborze uczelni ważne jest, aby wybrać to, w którym zostały stworzone odpowiednie warunki, aby uzyskać wysokiej jakości edukacji i wszechstronnego rozwoju osobowości. W podobny zaleceń odpowiada Buriacji uniwersytet państwowy...
Видовременная forma czasownika w języku angielskim. Tabela form czasowników języka angielskiego
Czasownik zmienia się w zależności od tego, w jakim czasie jest on stosowany. Czasy czasowników w języku angielskim, jak i rosyjskim, są podzielone na trzy główne kategorie ó przeszłość, teraźniejszość i przyszłość. Również...
Piramidy w Chinach – zagadki ludzkości
Piramidy w Chinach i po dziś dzień pozostaje tajemnicą dla ludzkości. Je rozwiązać zagadkę nie udało się jeszcze nikomu. Cały świat dowiedział się o istnieniu tych piramid stosunkowo niedawno. Dopiero w połowie 20 wieku zdjęcia te...
Powstanie dekabrystów: przyczyny porażki
Powstanie dekabrystów 1825 roku – jest to jedno z niewielu wydarzeń w historii naszego kraju, o którym wiedzą wszyscy jej mieszkańcy. W ogólnych zarysach prawie każdy wyobraża sobie, co to było za wydarzenie, czym to b...




















Uwaga (0)
Ten artykuł nie ma komentarzy, bądź pierwszy!