La función de distribución de una variable aleatoria. Cómo encontrar la función de distribución de una variable aleatoria
Para encontrar la función de distribución de variables aleatorias y sus variables, es necesario estudiar todas las características de esta área de conocimiento. Hay varios métodos diferentes para encontrar considerados de valores, incluyendo el cambio de la variable y la generación del momento. La distribución es un concepto inspirado en elementos tales como la varianza de las variaciones. Sin embargo, se caracterizan sólo la medida de la magnitud de la dispersión.

Más importantes de las funciones de variables aleatorias son aquellos que están relacionados y son independientes e igualmente distribuidas. Por ejemplo, si X1 es el peso de un individuo seleccionado aleatoriamente de la población de machos, X2 - peso de otro, ..., Xn - el peso de una persona de la población masculina, entonces, debe saber, como una función de X se distribuye. En este caso, se aplica el clásico teorema, llamado límite central. Permite mostrar que si n grande, la función debe estándar распределениям.
Características de una variable aleatoria
El teorema del límite central está diseñado para aproximarse discretos definidos los valores, tales como биномиальное y de poisson. Funciones de distribución de variables aleatorias, se examinan, en primer lugar, en simples valores de una variable. Por ejemplo, si X es continua aleatoria el valor que tiene su propia distribución de probabilidad. En este caso, se analiza cómo encontrar la función de densidad de Y, a través de dos enfoques diferentes, a saber, el método de la función de distribución y de los cambios de la variable. Primero sólo se tratan mutuamente valores únicos. A continuación, se debe modificar la técnica de cambio de variable, para encontrar su probabilidad. Por último, es necesario conocer como la inversa de la función de distribución acumulativa puede ayudar a modelar números aleatorios que siguen ciertos sucesivos esquemas.
Más:
El general walter von Reichenau: su biografía, sus logros y la historia
El General mariscal de campo de la alemania nazi walter von Reichenau (Walter von Reichenau) se contaba entre los pocos altos oficiales del ejército de la wehrmacht, que apoyó activamente el nazismo. Durante la Segunda guerra mundial fue comandante d...
Trajes espaciales de los astronautas: de la asignación de la unidad. El primer traje espacial
Trajes espaciales de los astronautas – no es simplemente trajes de vuelo en órbita. El primero de ellos se remonta a principios del siglo veinte. Era la época de antes de los vuelos espaciales restaba casi medio siglo. Sin embargo, los científi...
Oriental de la plataforma europea: forma de alivio. Minerales oriental de la plataforma europea
La Mayor parte del territorio europeo de rusia, así como de algunos países de la cei se encuentra en la parte continental de un tramo de la corteza terrestre, que lleva el nombre oriental de la plataforma europea. La forma del relieve aquí es predomi...
La Metodología de asignación definidos los valores de
El Método de la función de distribución de probabilidad de una variable aleatoria se aplica para encontrar su densidad. Cuando utiliza este método, se calcula acumulada valor. Luego, diferenciándose de él, se puede obtener la función de densidad de probabilidad. Ahora, si hay un método de la función de distribución, se puede considerar un par de ejemplos. Supongamos que X – una variable aleatoria continua con una cierta densidad de probabilidad.
¿Cuál es la función de densidad de probabilidad de x2? Si mostrar o construir la gráfica de la función (parte superior derecha) y = x2, se puede señalar que es creciente X y 0 <y<1. Ahora es necesario utilizar el método para encontrar Y. el Primero se encuentra total acumulada de la función de distribución, sólo es necesario diferenciar para obtener la función de densidad de probabilidad. De esta manera, obtenemos: 0<y<1. El método de distribución implementado con éxito, para encontrar Y, cuando el S – la creciente función de X. por Cierto, f (y) se integra dentro de 1 sobre y.
En el último ejemplo, una mayor cautela utilizado para la indización acumulativos y funciones de densidad de probabilidad o con X o con Y, para especificar a qué variable aleatoria pertenecían. Por ejemplo, cuando se encuentre la función de distribución acumulativa Y recibieron X. Si desea encontrar aleatoria el valor de X y de su densidad, lo que tan sólo es necesario diferenciar.
La Técnica de cambio de variables
Supongamos Que X – una variable aleatoria continua definida la función de distribución con el común denominador de f (x). En este caso, si se coloca un valor de y en X = v (Y), se obtiene el valor de x, por ejemplo, v (y). Ahora, es necesario obtener la función de distribución continua de una variable aleatoria Y. Donde la primera y la segunda igualdad tiene lugar a partir de la definición acumulativa Y. la Tercera igualdad se cumple debido a que parte de la función u (X) ≤ y, también es cierto que X ≤ v (Y). Y por último se realiza para determinar la probabilidad continua aleatorio más grande X. Ahora es necesario tomar la derivada de FY (y), la función de distribución acumulativa Y, para obtener la función de densidad de probabilidad de Y.
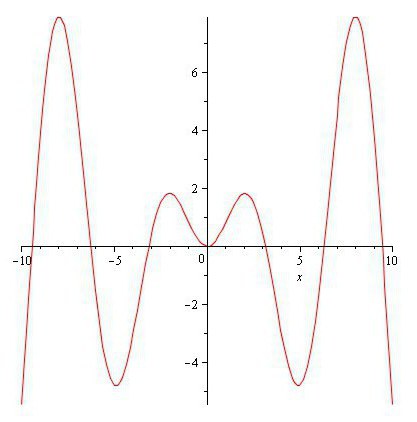
Síntesis de la función de reducción de
Supongamos Que X – una variable aleatoria continua con el total de f (x) definida sobre c1<x<c2. Y que Y = u (X) – menguante función de X inversa X = v (Y). Dado que la función es continua y se van, existe la función inversa X = v (Y).
Para abordar esta cuestión, se pueden recoger datos cuantitativos y utilizar empírica кумулятивную la función de distribución. Con esta información y apelando a ella, hay que combinar las muestras de los medios, la desviación estándar, medios y así sucesivamente.
De manera Similar, bastante simple modelo probabilístico puede tener un gran número de resultados. Si, por ejemplo, lanzar una moneda 332 veces. Entonces el número de los resultados de golpes de estado mayor, que el de google (10100) – el número, pero no menos de 100 квинтиллионов veces mayor a la de las partículas elementales en el universo conocido. No es interesante el análisis que da respuesta a cada resultado posible. Se requiere más simple concepto, tal como el número de cabezas o de más largo recorrido de colas. Con el fin de centrar la atención en las cuestiones de interés, se toma un cierto resultado. La definición en este caso la siguiente: variable aleatoria es real en función de probabilística del espacio.
La Gama S de una variable aleatoria a veces se denomina espacio de estados. Por lo tanto, si X- se analiza el valor de lo que N = X2, exp ↵X, X2 + 1, tan2 X, bXc y así sucesivamente. El último de ellos, redondeando X al entero más cercano, se llama la función de sexo.
La Función de distribución de
Una vez determinada la que interesa la función de distribución de una variable aleatoria x, la pregunta que normalmente se convierte en la siguiente: «cuál es la probabilidad de que X se mete en algún subconjunto de los valores de B?». Por ejemplo, B = {números impares}, B = {más 1} o B = {entre el 2 y el 7} para especificar estos resultados, que son de X, el valor de una variable aleatoria, en un subconjunto de a. Por lo tanto, en el ejemplo anterior, se puede describir el suceso de la siguiente manera.
{X es un número impar}, {X más 1} = {X> 1}, {X está entre 2 y 7} = {2 <X <7}, para que coincida con las tres variantes de arriba para un subconjunto de B. Muchas de las propiedades de variables aleatorias no están muy relacionados con un determinado X., más bien, depende de como X distribuye sus valores. Esto lleva a la definición, que es el siguiente: la función de distribución de una variable aleatoria x acumulados y se determina la cantidad de observaciones.
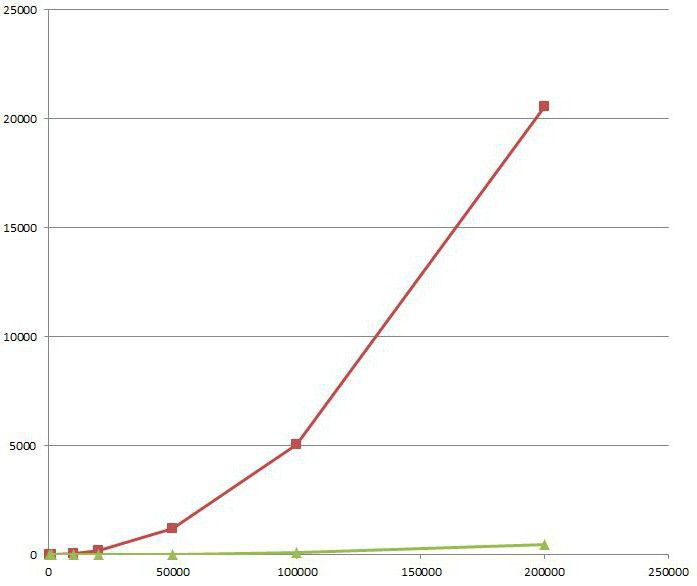
Las variables Aleatorias y funciones de distribución de
Por lo tanto, se puede calcular la probabilidad de que la función de distribución de una variable aleatoria x tome valores en el intervalo restando. Se debe pensar en la inclusión o exclusión de los extremos.
Vamos a llamar a la variable aleatoria discreta, si tiene final o de счетное infinito espacio de estados. Por lo tanto, X es el número de cabezas en tres independientes флипсах sesgada de la moneda, que se eleva con una probabilidad de p. Necesita encontrar кумулятивную la función de distribución de una variable aleatoria discreta FX para X. supongamos Que X es el número de picos en la colección de las tres cartas. Entonces Y = X3 a través de FX. FX comienza con 0, termina en 1 y no disminuye con el aumento de los valores de x. Total acumulada FX función de distribución de una variable aleatoria discreta X es constante, excepto en los saltos. Cuando se descarga FX es continua. Demostrar la afirmación correcta de la continuidad de la función de distribución de la propiedad de la probabilidad es posible con la ayuda de la definición. Suena así: una variable aleatoria tiene кумулятивную FX, que дифференцируема.
Para mostrar cómo puede ocurrir esto, se puede citar el ejemplo: el blanco con una sola radio. Supuestamente. el dardo se distribuye uniformemente en el área especificada. Para un λ> 0. Por lo tanto, las funciones de distribución de variables aleatorias continuas sin problemas aumentan. FX tiene las propiedades de la función de distribución.
El Hombre espera en la parada, hasta que no llegue. Al que niega, cuando se espera llegue a 20 minutos en coche. Es necesario encontrar кумулятивную la función de distribución de T. cuando la persona todavía se está en la estación de autobuses o no va a desaparecer. A pesar de que el total acumulada de la función de distribución de determinar para cada una variable aleatoria. De todos modos, con la frecuencia suficiente, se utilizarán otras características: peso para la dispersión de la variable y la función de densidad de probabilidad de una variable aleatoria. Normalmente, muestra a través de uno de estos dos valores.
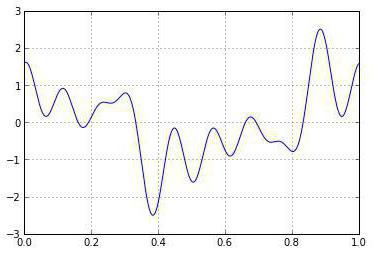
Masivas características
Estos valores se consideran las siguientes propiedades, que tienen el carácter masivo). La primera se basa en el hecho de que la probabilidad no son negativos. El segundo se desprende de la observación de que el conjunto de todos los x=2S, el espacio de estados X, forma la división de análisis probabilista de la libertad de X. Ejemplo: lanzamientos sesgada de la moneda, cuyos resultados son independientes. Se puede continuar con el cumplimiento de ciertas acciones, hasta que no pasa una tirada de goles. Supongamos que X es aleatoria valor que nos da la cantidad de colas antes de la primera cabeza. Y p representa la probabilidad de que en cualquier valor de la acción.
Por lo tanto, la función de probabilidad tiene los siguientes rasgos característicos. Debido a que los miembros forman la secuencia numérica, X se llama manera aleatoria el valor. Geométrica esquema c, cr, cr2,. , , , crn tiene cantidad. Y, por lo tanto, sn tiene un límite cuando n 1. En este caso, la infinita cantidad es el límite.
La Función de masa encima de la forma geométrica de la secuencia con la relación. Por lo tanto, de números naturales a y b. La diferencia de los valores en la función de distribución es igual al valor de los medios de opciones.
Pendientes de los valores de densidad tienen una definición: X es variable aleatoria, distribución de FX que tiene derivada. FX que satisface Z xFX (x) = fX (t) dt-1, se denomina función de densidad de probabilidad. Y X se denomina continua aleatoria de valor. El principal teorema de cálculo de la función de densidad es la derivada de la distribución. Se puede calcular la probabilidad mediante el cálculo de las integrales definidas.
Debido a que se recopilan datos a través de varias observaciones, debe ser considerado más de una de una variable aleatoria a la vez, para modelar los procedimientos experimentales. Por lo tanto, muchos de estos valores y su participación en la distribución de dos variables X1 y X2 significa visor de eventos. Para discretas variables aleatorias se definen conjuntos probabilísticos de masas de la función. Para continuas se describen fX1, X2, donde el conjunto de la función de densidad de probabilidad que se satisface.
Independientes de las variables aleatorias
Dos casual valores X1 y X2 son independientes, si cualquiera de los dos asociados eventos de la misma. En las palabras de la probabilidad de que dos eventos {X1 2 B1} y {X2 2 B2} se producen al mismo tiempo,y es igual a la multiplicación de las variables mencionadas anteriormente, que cada uno de ellos es individual. Para los independientes discretas variables aleatorias hay un conjunto probabilístico masiva de la función, que es una obra con el límite de los iones. Para continuos variables aleatorias son independientes, conjunta de la función de densidad de probabilidad - la obra de los valores límite de la densidad. En conclusión, se consideran n independientes de observaciones x1, x2,. , , , xn, surgen de la desconocida densidad o medios de la función f. Por ejemplo, un parámetro desconocido en las funciones para exponencial de una variable aleatoria que describe el tiempo de espera del autobús.
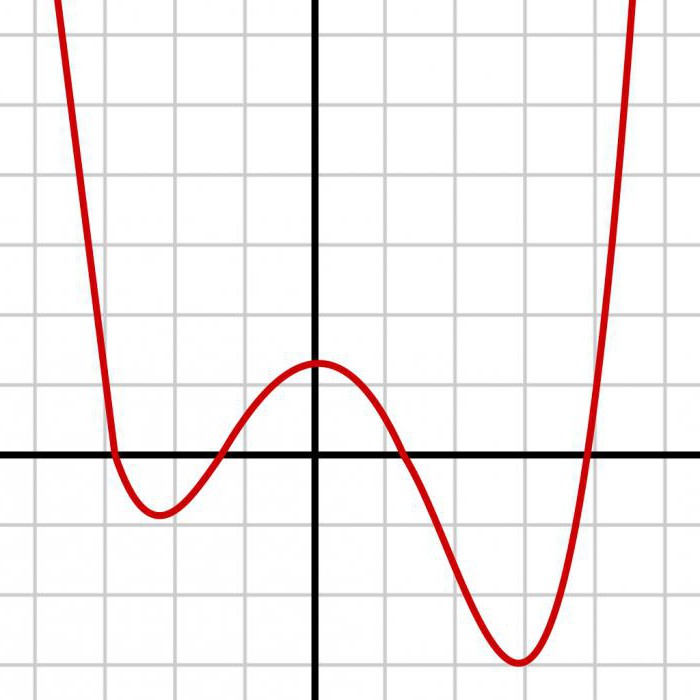
La Simulación de las variables aleatorias
El objetivo Principal de esta teórica de la zona – proporcionar las herramientas necesarias para desarrollar умозаключительных procedimientos basados en fundamentadas en los principios de la ciencia estadística. Por lo tanto, uno de los muy importantes casos de uso del software es su capacidad para generar псевдоданные para la simulación real de la información. Esto le da la oportunidad de probar y mejorar los métodos de análisis antes de la necesidad de la utilización de sus reales en las bases. Esto es necesario para que investigaban las propiedades de los datos a través de la simulación. Para muchos utilizadas colecciones de variables aleatorias R proporciona comandos para su creación. Para otras circunstancias se necesitarán métodos de simulación de la secuencia de variables aleatorias independientes que tienen en común la distribución.
Las variables aleatorias Discretas y el patrón Command. Sample se utiliza para crear simples y estratificados de muestras aleatorias. En consecuencia, si se introduce la secuencia x, sample (x, 40) elige 40 entradas de x de tal manera que todas las opciones de tamaño de 40 tienen la misma probabilidad de ganar. Esto se utiliza el comando R predeterminado para el muestreo sin reemplazo. También se puede utilizar para la simulación discreta de valores aleatorios. Para ello, es necesario proporcionar el espacio de estados en el vector x y medios de la función f. La llamada para replace = TRUE indica que el muestreo se produce con la sustitución. Luego de dar una muestra de n variables aleatorias independientes que comparten masiva de la función f, se utiliza la muestra (x, n, replace = TRUE, prob = f).
Se ha indicado, que el 1 es el menor representado por el valor y el 4 es el más grande de todos. Si el comando prob = f omitida, es una muestra de elegir el uniforme de los valores en el vector x. Comprobar la simulación en contra de medios de la función que genere datos, se puede enfatizar en el carácter doble de la igualdad, ==. Y reformulado después de calcular la observación, que toman cada posible valor de x. Se puede hacer una tabla. Repita esto para 1000 y comparar la simulación con la función apropiada de la masa.
Ilustración de la transformación de la probabilidad
En primer lugar modelar homogéneos funciones de distribución de variables aleatorias u1, u2,. , , , un en el intervalo [0, 1]. Aproximadamente el 10 % de los números debe estar en el intervalo [0,3, 0,4]. Esto corresponde a un 10 % de las simulaciones en el intervalo [0,28, 0,38] para una variable aleatoria con la que se muestra la función de distribución FX. De la misma manera alrededor del 10% de números aleatorios debe estar en el intervalo [0,7, 0,8]. Esto corresponde a un 10 % de las simulaciones en el intervalo [0,96, 1,51] de una variable aleatoria con función de distribución FX. Estos valores en el eje x se puede obtener de la toma de la inversa de FX. Si X es una variable aleatoria continua con densidad fX, positiva en todas partes en su área, entonces la función de distribución estrictamente creciente. En este caso, el FX tiene una función inversa FX-1, conocida como la función de квантиля. FX (x) u sólo entonces, cuando x FX-1 (u). La transformación de la probabilidad debe partir del análisis de la variable aleatoria U = FX (X).
FX tiene un rango de 0 a 1. Él no puede tomar un valor por debajo de 0 o por encima de 1. Para valores de u entre 0 y 1. Si se puede simular la U, debe imitar y aleatoria de la distribución FX a través de la función квантиля. Tomar la derivada, para ver que la función de densidad de u varía de menos de 1. Dado que la variable aleatoria U tiene una densidad constante en un intervalo de sus valores posibles, se dice que es uniforme en el intervalo [0, 1]. Él es simulado en R mediante el comando runif. La identidad se llama probabilística de la conversión. Se ve como funciona en el ejemplo de la дротильной de la tabla. X entre 0 y 1, la función de distribución de u = FX (x) = x2, y, por lo tanto, la función de квантиля x = FX-1 (u). Puede simular los efectos independientes de la observación de la distancia desde el centro de la barra de un dardo, y creando de este modo uniforme casual valores de U1, U2,. , , Un. La función de distribución de y empírica se basan en el 100 симуляциях distribución de dardos. Para la exponencial de una variable aleatoria, supuestamente u = FX (x) = 1 - exp (- x), y, por lo tanto, x = - 1 ln (1 - u). A veces la lógica se compone de equivalentes de notificaciones. En este caso, es necesario unir las dos partes del argumento. La identidad con la intersección de una manera similar para todos los 2 {S i} S, en lugar de un valor. La combinación de Ci es igual a espacio de estados S y cada pareja mutuamente excluida. Ya Bi - se divide en tres axiomas. Cada prueba se basa en la probabilidad de P. Para cualquier subconjunto. Usando la identidad, para asegurarse de que la respuesta no depende de si se incluyen los extremos del intervalo.
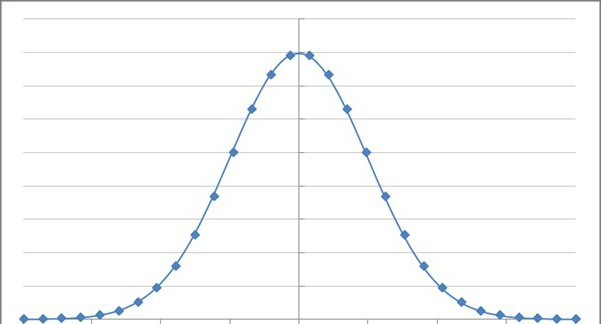
La función Exponencial y sus variables
Para cada uno deel resultado en todos los eventos, en última instancia, se utiliza una segunda propiedad de la continuidad de la probabilidad que se considera аксиоматическим. La ley de la distribución de funciones de una variable aleatoria aquí muestra que cada uno de su decisión y respuesta.
Article in other languages:

Alin Trodden - autor del artículo, editor
"Hola, soy Alin Trodden. Escribo textos, leo libros y busco impresiones. Y no soy mala para decírtelo. Siempre estoy feliz de participar en proyectos interesantes."
Noticias Relacionadas Con La
Cómo traducir киловатты en caballos de fuerza
Esta medida, como un caballo de fuerza, se utiliza en nuestro país para determinar la potencia de hace mucho tiempo, convirtiéndose en habitual y comprensible. Sin embargo, un número creciente de estados, incluyendo rusia, renunci...
El piloto stepán mikoyan: biografía, fotos
stepán mikoyan – soviética de la prueba piloto, авиаконструктор, Héroe de la unión soviética, caballero de las órdenes de lenin y de la bandera roja, toda la vida se ha relacionado con los aviones. El responsable de la admin...
Médico-cirujano, leonid Рогозов: biografía y foto
leonid Рогозов famoso en todo el mundo. El cirujano de la especialidad, impone equilibrio por sí mismo en un cojín. La cirugía para extirpar el apéndice inflamado se prolongó durante 1,5 horas. Nuestro artículo está dedicado a la ...
Escuela de autogestión – ¿cuál es su función?
Escolar autonoma – es bastante viejo sistema, existente en cada escuela. Nacido aún en la época soviética. Sin embargo, el trabajo soviética autonoma escolar era bastante diferente de la actual.¿y qué la diferencia? En la ép...
Mirando en el diccionario: mal educado – que es esto?
el ruso Moderno, en gran medida, diferente a lo que ellos usaban nuestros antepasados más de cien años atrás. Viva y dinámica, cambia con la sociedad. Al estudiar, por ejemplo, el léxico de la composición del discurso, se puede co...
la central nuclear de chernobyl. S. I. lenin – el ucraniano de la central, прекратившая su trabajo en relación con la explosión de la энергоблоке nº 4. Su construcción comenzó en la primavera de 1970, y después de 7 años que...






















Comentarios (0)
Este artículo no tiene comentarios, se el primero!