パスカルの三角形です。 特性のパスカルの三角形

ヒトの進捗が増加し、前期に比べ増収となり発見した人の天才の時代で、天才です。 その一つがブレーズパスカルです。 彼の経歴を確認し、真実の表現ライオンFeuchtwanger“優秀な人材のすべ”ます。 すべての科学的成果本研究では困難な列挙します。 そのなかで最も優雅な発明が数学の世界-パスカルの三角形します。

つ天才行

ブレーズパスカルの近代的な基準は死亡した、早期の年齢39歳ます。 しかし、その短い生活のた証人としての優れた物理学者の数学者、哲学者、ライター。 感謝の子孫の名前には彼の名誉を、ユニットの圧力や人気のパスカルプログラミング言語です。 そうになったということ60歳までの教育の場となるに違いない。 例えば、いつもお世話になって、学生がプログラムを計算するための三角の""Pascal"は、どの性質を探求しの方には、後述のとおりです。

なお、この研究者との特別な思考に対して，多様な分野の科学です。 特に、ブレーズパスカルは、創設者の一人であるhydrostatics数理解析では、複数の領域の幾何学と確率論です。 また、

• 作成した機械式計算機として知られるPaskaleva輪;
• 表を実証する空気は、弾力性と重量;
• このバロメーターを予測することができ、天候;
• を発明した手押し車;
• 発明されたオムニバス—馬車と固定路線 初の定期公共交通機関などです。

演算パスカルの三角

と言われているので、このフランスの研究者が多大な貢献をしてきた数理科学です。 彼の絶対名品の科学“論文の演算の三角形で構成される二項の係数に配置され、特定の順序です。 は、この制度はありますが、驚くほど様々であり、彼女は確認の考“すべての輝かしい&mdashが簡単です。rdquo;ります。

以上

神経インパルス,その変換と伝達機構

人間の神経系としてのコーディネーターになります。 いろいろなものを発信コマンドからの脳の筋肉、臓器、組織、プロセスの信号が来ています。 どのようなデータの中の神経インパルス. 何ですか？ スピードす。 これらの数に基づく総合的質疑応答えないことを示しています。う神経インパルス?という波の励起とスプレッドの繊維としての対応刺激の神経細胞となる。 このメカニズムが確実に情報伝達から各種受容体のきるようになりました。 そして、異なる臓器(筋肉や腺). どこのプロセスを表す生理はどうすればいいですか？ ...

ピラミッドと中国人のジレンマ

ピラミッドの中、この日は謎できます。 その謎のが一番いいと思います。 世界の存在を知りこれらのピラミッドです。 に20世紀絵画の奇跡でしたからとられます。 そして人類の知 このピラミッドが存在した。 今日でも、これらの宝物の世界の文化を厳重に保護されて政府はこの国です。ただし、ピラミッドの中国にとって大きな関心事項の多くの研究者と考古学者. 言い伝えでは、既存のがこの国のピラミッド、外国人の人が訪れています。 の正確な年齢のこれらの独自の構造を、誰もが知っています。 最初の情報について...

のDecembrist蜂起の原因の敗北

 乱のDecembristsに1825–数のイベントに、我が国ることが知られているすべてます。 一般に、ウズベキスタンのほとんどの人が想像するこのイベントで何を終了しました。 多くの歴史学者に捧げてその活動の研究ではこの素晴らしい。すべてのDecembrist反乱が大きな影響を与えるのは、国家開発の一部のものが多いと感じている今日のイベントの結果何が起きたのか、元老院広場があります。[rek1]まず、その原因Decembrist乱. そして、もちろん、人を忘れて、戦争の18...

少し歴史

公ているとは言えこパスカルの三角知られていたヨーロッパの16世紀初頭ます。 特に、その画像で見ることのできるカバーの教科書の計算には、有名な天文学者ピーター ApianからIngoldstadt大学です。 類似の三角形として図書中国の数学者Yang輝、1303ます。 彼の性質を知られていたも偉大なペルシャの詩人で哲学者マルハイヤーム12世紀初頭ます。 また、そのた知られていた論文のアラビア語とインドの学者が記述します。

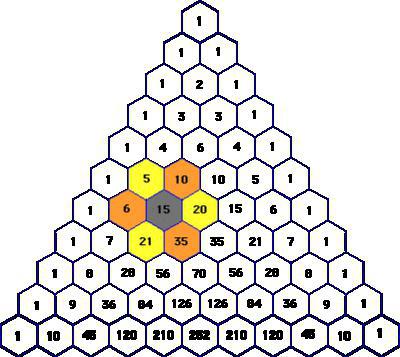
解説

前までの興味深い特性を持つのパスカルの三角形はその完成度を簡単のために知っておくべきことは何であります。

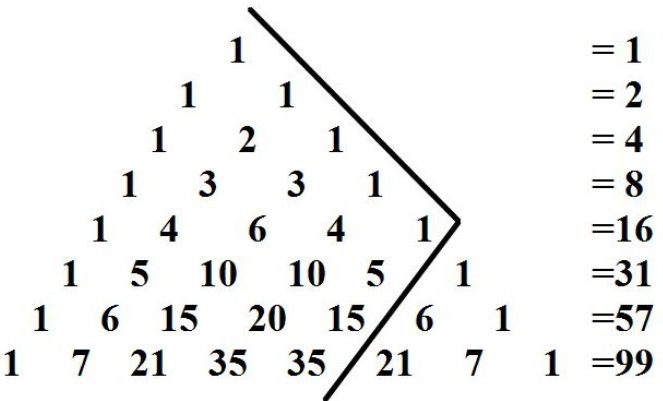
を科学的に言えば、この数値スキームの無限テーブルが三角形で構成されてい二項の係数に配置され、特定の順序です。 その上面番号1です。 その他のポジションの数と同一の数の合計数を上します。 この場合、すべての列のパスカルの三角形が対称対の垂直軸ます。

主要な物件について

Pascalの三角形が印象的なその完成度です。 任意の行数n(n=0,1,2…)true:

• 最初と最後の番号—1;
• 第penultimate—n;
• 第三号三角数のサークルできるフォームに配置されているのは、正三角形、すなわち, 1, 3, 6, 10): T_N-1=n(n-1)/2になります。
• の数は四面体あるいはピラミッドと三角形になります。

また、比較的最近では、1972年にはまた別の物件のパスカルの三角形です。 検出可能なので、記述する必要がありますの要素をこのスキームの形式でテーブル行のシフトを2の位置ます。 そこでマークの数で割り切れの行番号です。 ここで示されているデータの数のカラムの選択数が素数です。

と同じトリックができるとは異なります。 このパスカル三角形の数字の残りの部のライン番号を表します。 そしてラインによる三角形に次の開始右2列から最初の要素のつようになりました。 その柱としている番号の素数は、のみをゼロとの方が合成が含まれまで少なくとも一つのゼロになります。

との接続は二項の定理にあたって

これは、いわゆる数式の解の全体に非負の和の二つの変数の形式

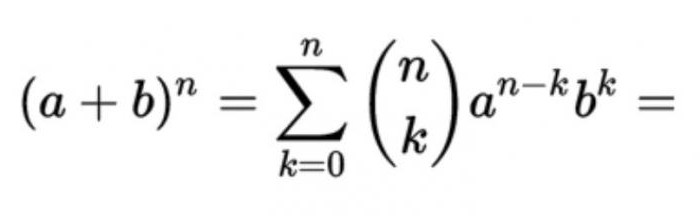
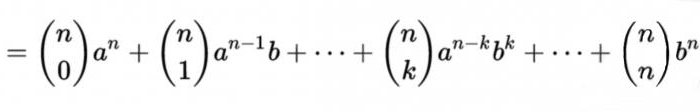
現在の係数に等しいC_N=n! /(mです！ (n-m)!), mの序数の数字列nのパスカルの三角形です。 つまり、この構造を定義しなければいけませんので簡単に上げる為に配置しております。

では、パスカルの三角の二項の定理の相互関係と密接なります。

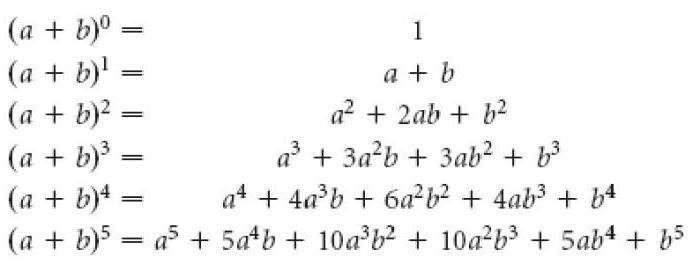
数奇跡

注意深い研究のパスカルの三角形をよく目にすることでしょうがあります:

• 全ての数字の列を配列番号n(数0) 以上2^N;
• ライン左揃えで、その金額の数字をdiagonalsのパスカルの三角形から下、左から右に、同フィボナッチ数列;
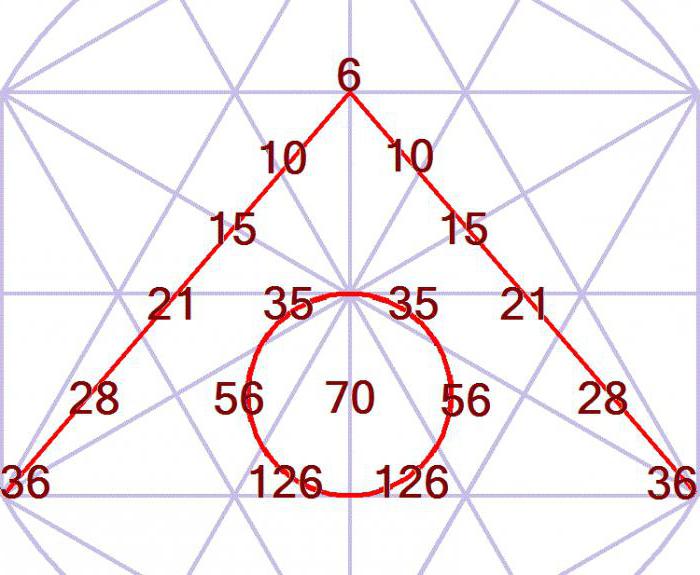
• "対角"の自然数の順;
• のいずれかの項目からのパスカルのトライアングル 削減原単位等のすべての番号の中にある平行四辺形囲左右diagonals交差するここ数;
• 各行の図の数の総和をも場所に等しいと、和の要素が奇数の場所です。

Sierpinski三角

などに興味深い数理スキームは非常に有望視点からの解決の複雑なタスクが出た場合、塗装も数Paskaleva像の色は、単元未満別します。

Sierpinski三角形をセットアップすることで別の方法：

• シャドーは図のパスカルrepaint異なる色の三角形による接続の中点の側面の原;
• 同様に、この法律の未塗装置の隅々ます。
• その場合は無期限に継続、結果と鳴ります。

最も興味深い特徴のSierpinski三角—その自己相似性は、より成り立っていますので3部と減の2倍です。 できるこのスキームのフラクタル曲線、およって最新の研究に最適の数理モデリングの雲、植物、川の中州には、宇宙そのものです。

つかの興味深い課題

を使用したパスカルの三角形か？ 例の課題を解決することができ、それは非常に多様ならびに所属し異なる分野の科学です。 考えてものの中で最も興味深いものにします。

問題の1です。 一部の大都市に囲まれた壁と、入り口ゲートがあります。 では、最初の交差点で、主要道路半導体レーザの出力は大きく拡散します。 同じ起こること。 の市210人ます。 それぞれの共通の交差点であるといわれている。 どのよう多くの人にご相談いただける各交差点が共有クリックするとnhkサイトを離します。 彼女の答えは、10rowのパスカルの三角形式の係数れまで述べてきたさまざまな場面の縦軸の数210します。

タスク2です。 ある7種類のメーカー。 が必要で花束の3花ます。 たいどのように多くの異なる方法で行うことができます。 この問題の組合せ論します。 その解決のための、パスカルの三角形、7の文字列の位置番号の両方の場合は0)35まで拡大してまいります。

現在を知ることによって発明され、フランスの哲学者、科学者のパスカルです。 彼の有名な三角形、正常に利用できる真のようにしてほ多くの課題、特に分野組合せ論します。 また、利用することができる解決に多くの謎に伴うフラクタルです。