Now - 17:23:02
Трохкутнік Паскаля. Ўласцівасці трыкутніка Паскаля
Прагрэс чалавецтва шмат у чым звязаны з адкрыццямі, зробленымі геніямі. Адным з іх з'яўляецца Блез Паскаль. Яго творчая біяграфія яшчэ раз пацвярджае праўдзівасць выказвання Ліёна Фейхтвангера «Таленавіты чалавек, таленавіты ва ўсім». Усе навуковыя дасягненні гэтага вялікага навукоўца цяжка пералічыць. Да іх ліку адносіцца адно з самых элегантных вынаходак ў свеце матэматыкі — трохкутнік Паскаля.

Некалькі слоў аб геніі
Блез Паскаль па сучасных мерках памёр рана, ва ўзросце 39 гадоў. Аднак за сваё кароткае жыццё ён праявіў сябе як выбітны фізік, матэматык, філосаф і пісьменнік. Удзячныя нашчадкі назвалі ў яго гонар адзінку ціску і папулярны мова праграмавання Pascal. Ён ужо амаль 60 гадоў выкарыстоўваецца для навучання напісання розных кодаў. Напрыклад, з яго дапамогай кожны школьнік можа напісаць праграму для вылічэння плошчы трохвугольніка на «Паскалю», а таксама даследаваць ўласцівасці схемы, аб якой гаворка пойдзе ніжэй.
Дзейнасць гэтага вучонага з экстраардынарным мысленнем ахоплівае самыя розныя вобласці навукі. У прыватнасці, Блез Паскаль з'яўляецца адным з заснавальнікаў гидростатики матэматычнага аналізу, некаторых напрамкаў геаметрыі і тэорыі верагоднасцяў. Акрамя таго, ён:
- стварыў механічны калькулятар, вядомы пад назвай Паскалева колы;
- прадставіў эксперыментальнае доказ таго, што паветра валодае пругкасцю і мае вагу;
- усталяваў, што барометр можна выкарыстоўваць для прадказання надвор'я;
- вынайшаў тачку;
- прыдумаў амнібус — конныя экіпажы з фіксаванымі маршрутамі, якія сталі пасля першым выглядам рэгулярнага грамадскага транспарту і інш.
Арыфметычны трохкутнік Паскаля
Як ужо было сказана, гэты вялікі французскі вучоны ўнёс вялікі ўклад у матэматычную навуку. Адным з яго безумоўных навуковых шэдэўраў з'яўляецца «Трактат аб арыфметычным трыкутніку», які складаецца з биномиальных каэфіцыентаў, расстаўленых у пэўным парадку. Ўласцівасці гэтай схемы дзівяць сваім разнастайнасцю, а сама яна пацвярджае прыказку «Усе геніяльнае — проста!».
Больш:
Нервовы імпульс, яго пераўтварэнне і механізм перадачы
Нервовая сістэма чалавека выступае своеасаблівым каардынатарам у нашым арганізме. Яна перадае каманды ад мозгу мускулатуры, органаў, тканін і апрацоўвае сігналы, якія ідуць ад іх. У якасці своеасаблівага носьбіта дадзеных выкарыстоўваецца нервовы імп...
Куды паступаць пасля 11 класа? Якую выбраць прафесію?
Пры выбары сваёй будучай прафесіі не варта абапірацца на чые-то рэкамендацыі і парады, тым больш не трэба падпарадкоўвацца сваім бацькам, якія даволі часта вырашаюць без вас самастойна, куды паступіць пасля 11 класа. Варта задумацца, наколькі паспяхо...
Крывяносная сістэма жывёл, як вынік эвалюцыйнага развіцця свету
Крывяносная сістэма жывёл прайшла доўгі шлях фарміравання ў ходзе эвалюцыйнага развіцця свету. Яна ўтварылася на месцы рудыментарных частак першаснай паражніны цела, якая ў вышэйшых жывёл была выцесненая целломом, або другаснай паражніной цела. У пра...
Трохі гісторыі
Справядлівасці дзеля трэба сказаць, што на самай справе трохкутнік Паскаля быў вядомы ў Еўропе яшчэ ў пачатку 16 стагоддзя. У прыватнасці, яго малюнак можна ўбачыць на вокладцы падручніка арыфметыкі вядомага астранома Пятра Апиана з Ингольтштадского універсітэта. Падобны трохкутнік прадстаўлены і ў якасці ілюстрацыі ў кнізе кітайскага матэматыка Ян Хуэй, выдадзенай у 1303 годзе. Пра яго уласцівасцях было вядома таксама і выдатнаму персідскага паэту і філосафу Амару Хайям яшчэ ў пачатку 12 стагоддзя. Прычым лічыцца, што ён пазнаёміўся з ім з трактатаў арабскіх і індыйскіх навукоўцаў, напісаных раней.
Апісанне
Перш чым даследаваць цікавыя ўласцівасці трыкутніка Паскаля, прыгожага ў сваім дасканаласці і прастаце, варта даведацца, што ён з сябе ўяўляе.
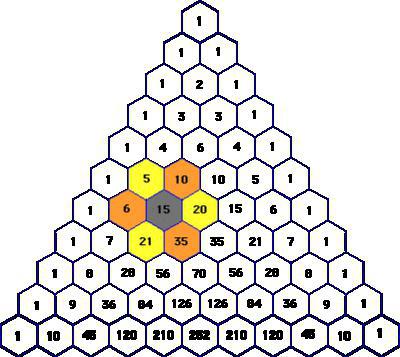
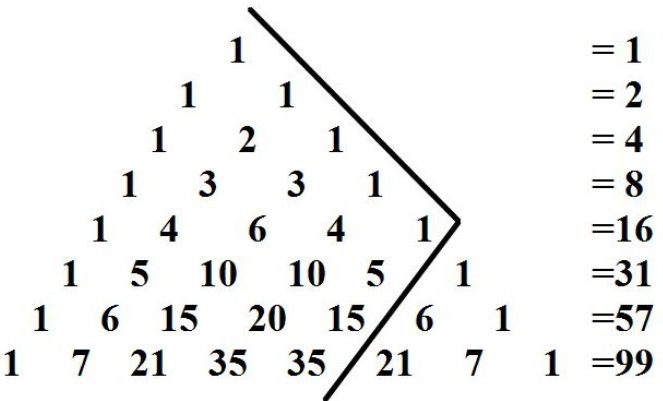
Кажучы навуковым мовай, гэтая лічбавая схема - бясконцая табліца трохкутнай формы, утвораная з биномиальных каэфіцыентаў, размешчаных у пэўным парадку. У яго вяршыні і па баках знаходзяцца лічбы 1. Астатнія пазіцыі займаюць колькасці, роўныя суме двух лікаў, размешчаных над імі побач вышэй. Пры гэтым усе радка трыкутніка Паскаля сіметрычныя адносна яго вертыкальнай восі.
Асноўныя ўласцівасці
Трыкутнік Паскаля дзівіць сваёй дасканаласцю. Для любой радкі пад нумарам n (n = 0, 1, 2…) дакладна:
- першае і апошняе колькасці — 1;
- другое і перадапошняе — n;
- трэцяе лік роўна треугольному колькасці (колькасці гурткоў, якія можна расставіць ў выглядзе роўнабаковага трыкутніка, т. е. 1, 3, 6, 10): Tн-1 = n (n - 1) / 2.
- чацвёртае лік з'яўляецца тетраэдрическим, г. зн. уяўляе сабой піраміду з трохвугольнікам ў падставе.
Акрамя таго, параўнальна нядаўна, у 1972 годзе, было ўстаноўлена яшчэ адно ўласцівасць трыкутніка Паскаля. Для таго каб яго выявіць, трэба запісаць элементы гэтай схемы ў выглядзе табліцы са зрухам радкоў на 2 пазіцыі. Затым адзначаюць лікі, дзеляцца на нумар радка. Аказваецца, што нумар слупка, у якім вылучаныя ўсе лікі, з'яўляецца простым лікам.
Той жа трук можна ажыццявіць і па-іншаму. Для гэтага ў трыкутніку Паскаля замяняюць ліку на рэшткі ад іх дзялення на нумар радка ў табліцы. Затым размяшчаюць радкі ў атрыманым трыкутніку так, каб наступная з іх пачыналася правей на 2 калонкі ад першага элемента папярэдняй. Тады слупкі, якія маюць нумары, якія з'яўляюцца простымі лікамі, будуць складацца толькі з нулёў, а ў тых, у якіх яны складовыя, будзе прысутнічаць хаця б адзін нуль.
Сувязь з биномом Ньютана
Як вядома, так называецца формула для раскладання на складнікі цэлай неадмоўнага ступені сумы двух зменных, якая мае выгляд:
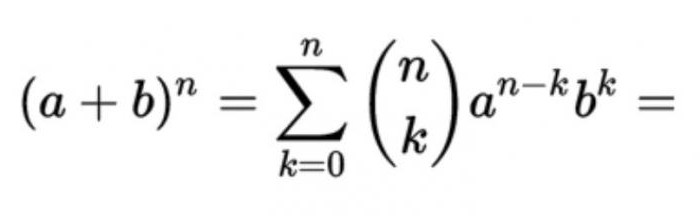
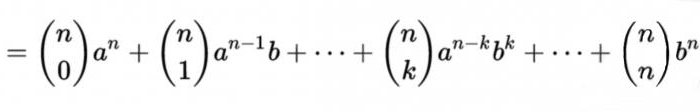
Прысутныя ў іх каэфіцыенты роўныя CNM = n! / (m! (n - m)!), дзе m, ўяўляе сабой парадкавы нумар лікі ў радку n трыкутніка Паскаля. Іншымі словамі, маючы пад рукой гэтую табліцу, можна лёгка ўзводзіць у ступень любыяколькасці, папярэдне расклаўшы іх на два складнікаў.
Такім чынам, трохкутнік Паскаля і біном Ньютана ўзаемазвязаны самым цесным чынам.
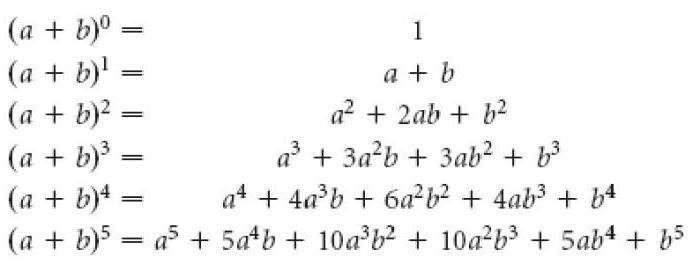
Матэматычныя цуды
Пры ўважлівым вывучэнні трыкутніка Паскаля можна выявіць, што:
- сума ўсіх лікаў у радку з парадкавым нумарам n (адлік вядзецца з 0) роўная 2п;
- калі радкі выраўнаваць па левым краі, то сумы лікаў, якія размешчаны ўздоўж дыяганаляў трыкутніка Паскаля, якія ідуць знізу ўверх і злева направа, роўныя лікаў Фібаначы;
- першая «дыяганаль» складаецца з натуральных лікаў, якія ідуць па парадку;
- любы элемент з трыкутніка Паскаля, паменшаны на адзінку, роўны суме ўсіх лікаў, размешчаных ўнутры паралелаграма, які абмежаваны левымі і правымі дыяганалямі, перасякальнымі на гэтым ліку;
- у кожнай радку схемы сума лікаў на цотных месцах роўная суме элементаў на няцотных месцах.
Трыкутніка Серпинского
Такая цікавая матэматычная схема, досыць перспектыўная з пункту гледжання вырашэння складаных задач, атрымліваецца, калі размаляваць цотныя лікі Паскалевого выявы ў адзін колер, а няцотныя — у іншы.
Трыкутніка Серпинского можна выбудаваць і іншым чынам:
- у зафарбаваным схеме Паскаля перафарбоўваюць ў іншы колер серединный трохкутнік, які адукаваны шляхам злучэння сярэдзін бакоў зыходнага;
- сапраўды таксама паступаюць з трыма незакрашенными, расположеными ў кутах;
- калі працэдуру працягваць бясконца, то ў выніку павінна атрымацца двухколерная фігура.
Самае цікавае ўласцівасць трыкутніка Серпинского — яго самоподобие, так як ён складаецца з 3-х сваіх копій, якія зменшаны ў 2 разы. Яно дазваляе аднесці гэтую схему да фрактальным крывым, а яны, як паказваюць найноўшыя даследаванні лепш за ўсё падыходзяць для матэматычнага мадэлявання аблокаў, раслін, дэльт рэк, ды і самой Сусвету.
Некалькі цікавых задач
Дзе выкарыстоўваецца трохкутнік Паскаля? Прыклады задач, якія можна вырашаць з яго дапамогай, досыць разнастайныя і ставяцца да розных абласцях навукі. Разгледзім некаторыя, найбольш цікавыя з іх.
Задача 1. У некаторага вялікага горада, абнесенага прыгоннай сцяной, толькі адны ўваходныя вароты. На першым скрыжаванні асноўная дарога разыходзіцца на дзве. Тое ж адбываецца і на любым іншым. У горад заходзяць 210 чалавек. На кожным з якія сустракаюцца скрыжаванняў яны дзеляцца папалам. Колькі чалавек будзе знаходзіць на кожным скрыжаванні, калі дзяліцца будзе ўжо немагчыма. Яе адказам з'яўляецца 10 радок трыкутніка Паскаля (формула каэфіцыентаў прадстаўлена вышэй), дзе па абодва бакі ад вертыкальнай восі размешчаны ліку 210.
Задача 2. Маецца 7 найменняў кветак. Трэба скласці букет з 3 кветак. Патрабуецца высветліць, колькімі рознымі спосабамі гэта можна зрабіць. Гэтая задача з вобласці курса: сфарміраваць. Для яе рашэння зноў жа выкарыстоўваем трохкутнік Паскаля і атрымліваем на 7 радку на трэцяй пазіцыі (нумарацыя ў абодвух выпадках з 0) лік 35.

Цяпер вы ведаеце, што вынайшаў вялікі французскі філосаф і вучоны Блез Паскаль. Яго знакаміты трохкутнік пры правільным выкарыстанні можа стаць сапраўднай палачкай-ратавалачкай для вырашэння мноства задач, асабліва з вобласці курса: сфарміраваць. Акрамя таго, яго магчыма выкарыстоўваць для разгадвання шматлікіх загадак, звязаных з фракталаў.
Article in other languages:
AR: https://tostpost.com/ar/education/129-pascal-s-triangle-properties-of-pascal-s-triangle.html
En: https://tostpost.com/education/387-pascal-s-triangle-properties-of-pascal-s-triangle.html
HI: https://tostpost.com/hi/education/129-pascal-s-triangle-properties-of-pascal-s-triangle.html
JA: https://tostpost.com/ja/education/128-pascal-s-triangle-properties-of-pascal-s-triangle.html
KK: https://tostpost.com/kk/b-l-m/218-shb-rysh-paskal-asietter-shb-rysh-paskal.html
PL: https://tostpost.com/pl/edukacja/221-tr-jk-t-pascala-w-a-ciwo-ci-tr-jk-ta-pascala.html
PT: https://tostpost.com/pt/educa-o/218-tri-ngulo-de-pascal-propriedades-do-tri-ngulo-de-pascal.html
TR: https://tostpost.com/tr/e-itim/224-gen-pascal-pascal-geni-zellikleri.html
UK: https://tostpost.com/uk/osv-ta/220-trikutnik-paskalya-vlastivost-trikutnika-paskalya.html
ZH: https://tostpost.com/zh/education/145-pascal-pascal.html

Alin Trodden - аўтар артыкула, рэдактар
"Прывітанне, Я Алін Тродден. Я пішу тэксты, чытаю кнігі і шукаю ўражанні. І я нядрэнна ўмею распавядаць вам пра гэта. Я заўсёды рады ўдзельнічаць у цікавых праектах."
Навіны
Кожны год 14 ліпеня французы адзначаюць Дзень узяцця Бастыліі. Свята вельмі своеасаблівы і даволі нечаканы. І каб разабрацца, з чым ён звязаны, неабходны невялікі экскурс у гісторыю. Магутная крэпасць, з высокімі сценамі і васьмю ...
Вытокі гістарычнага міфа, або для чаго вікінгам рагатую шлем
Для чаго вікінгам рагатую шлем? Сучасныя выявы нярэдка ўяўляюць гэтых сярэднявечных ваяроў лютымі і адчайнымі байцамі з вялікага памеру сякерамі і моцнымі даспехамі. Але для чаго вікінгам рагатую шлем? Бо ні для каго не сакрэт, шт...
Памылкі ва ўжыванні дзеяслова «апеляваць» - гэта вынік няправільнага тлумачэння словы
Дзеяслоў «апеляваць» - гэта запазычанае з замежнай мовы слова. Верагодна, таму яго ўжыванне звязана з распаўсюджанай маўленчай памылкай.Паходжанне словыСлова «апеляваць» паходзіць ад лацінскага appellare, ш...
Дзеці Кацярыны Вялікай. Праўленне і асабістае жыццё Кацярыны Вялікай
Руская імператрыца Кацярына Другая, вядомая таксама як Вялікая, панавала з 1762-га года па 1796-й. Ўласнымі намаганнямі яна істотна пашырыла Расійскую імперыю, значна палепшыла сістэму адміністравання і энергічна праводзіла паліты...
Мастацтва і навука. Дзеячы навукі і мастацтва
Калі зірнуць на шлях, які прайшло чалавецтва, можна казаць аб тым, што для прадстаўніка homo sapiens асноўнымі заўсёды былі тры задачы: выжываць, пазнаваць і ствараць. Калі ў дачыненні да першай пытанняў не ўзнікае наогул, то аста...
Віконт - гэта... Паходжанне тытула
Сярэднявечная дваранская іерархія застаецца для многіх нашых сучаснікаў складанай і заблытанай. У гэтым няма нічога дзіўнага, так як нават сярод сучаснікаў дваранскай шляхты нярэдка ўзнікалі рознагалоссі ў важнасці і самавітасці к...





















Заўвага (0)
Гэтая артыкул не мае каментароў, будзьце першым!