पास्कल त्रिकोण है. गुण के पास्कल के त्रिभुज

मानव प्रगति के कारण बड़े पैमाने पर की गई खोजों से प्रतिभाएँ. उनमें से एक है Blaise पास्कल. उनकी जीवनी पुष्टि की सच्चाई की अभिव्यक्ति शेर Feuchtwanger “एक प्रतिभाशाली व्यक्ति सब कुछ में प्रतिभाशाली है”. सभी वैज्ञानिक उपलब्धियों के इस महान वैज्ञानिक यह मुश्किल है को एन्यूमरेट करने के लिए. उनमें से एक है सबसे सुंदर आविष्कारों की दुनिया में गणित-पास्कल त्रिकोण है.

के बारे में कुछ शब्द प्रतिभा

Blaise पास्कल आधुनिक मानकों के द्वारा, वह जल्दी मृत्यु हो गई, में की उम्र 39 साल है । हालांकि, अपने छोटे से जीवन में उन्होंने खुद को साबित कर दिया के रूप में एक उत्कृष्ट भौतिक विज्ञानी, गणितज्ञ, दार्शनिक और लेखक है. आभारी वंश का नाम उनके सम्मान में इकाई के दबाव और लोकप्रिय पास्कल प्रोग्रामिंग भाषा है । वह गया था लगभग 60 साल की उम्र के इस्तेमाल को पढ़ाने के लिए लेखन की अलग-अलग कोड है । उदाहरण के लिए, उनकी मदद के साथ, हर छात्र एक प्रोग्राम लिख सकते हैं की गणना करने के लिए एक त्रिकोण के क्षेत्र पर "पास्कल", के रूप में अच्छी तरह के रूप में गुणों का पता लगाने की योजना है, जो नीचे चर्चा की जाएगी.

गतिविधियों के इस वैज्ञानिक के साथ असाधारण सोच को शामिल किया गया, बहुत ही विविध क्षेत्रों में विज्ञान है. विशेष रूप से, Blaise पास्कल के संस्थापकों में से एक hydrostatics गणितीय विश्लेषण, कई क्षेत्रों और ज्यामिति के सिद्धांत संभावना है. इसके अलावा, वह है:

<उल>

बनाया गया एक यांत्रिक कैलकुलेटर के रूप में जाना जाता Paskaleva पहिया;

प्रस्तुत प्रयोगात्मक सबूत है कि हवा लोच है और एक वजन;

में पाया गया कि बैरोमीटर इस्तेमाल किया जा सकता है की भविष्यवाणी करने के लिए मौसम के लिए;

का आविष्कार किया wheelbarrow;

का आविष्कार किया सर्वग्राही और mdash; घोड़े तैयार carriages के साथ फिक्स्ड मार्गों, जो बाद में बने पहले नियमित रूप से सार्वजनिक परिवहन, आदि.

गणित पास्कल त्रिभुज

के रूप में कहा गया है, इस महान फ्रांसीसी वैज्ञानिक ने एक बहुत बड़ा योगदान दिया करने के लिए गणितीय विज्ञान है. उनके एक निरपेक्ष कृतियों का विज्ञान है “ग्रंथ पर अंकगणितीय त्रिकोण" के होते हैं, जो binomial coefficients की व्यवस्था में एक विशेष आदेश है । के गुणों को इस योजना से अचरज विविध रहे हैं, और वह इस बात की पुष्टि कहावत “सभी प्रतिभाशाली और mdash; सरल! और rdquo;.

एक छोटे से इतिहास

मैं निष्पक्षता में कहना होगा कि वास्तव में पास्कल के त्रिभुज में जाना जाता था यूरोप में जल्दी 16 वीं सदी में । विशेष रूप से, अपनी छवि पर देखा जा सकता है कवर की पाठ्यपुस्तक गणित, प्रसिद्ध खगोल विज्ञानी पीटर Apian से Ingoldstadt विश्वविद्यालय है. इसी तरह के त्रिकोण के रूप में प्रस्तुत पुस्तक में चित्र द्वारा चीनी गणितज्ञ यांग हुई में प्रकाशित 1303. अपने गुण जाने जाते थे, यह भी एक महान फारसी कवि और दार्शनिक उमर खय्याम में जल्दी 12 वीं सदी है. इसके अलावा, यह माना जाता है कि वह था उसके साथ परिचित से ग्रंथ अरबी और भारतीय विद्वानों ने लिखा है.

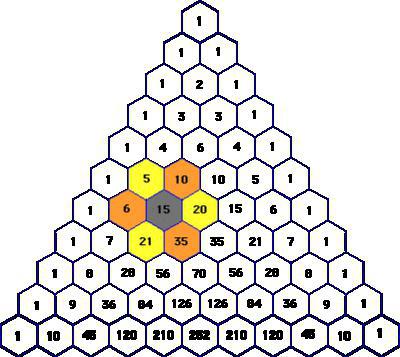
विवरण

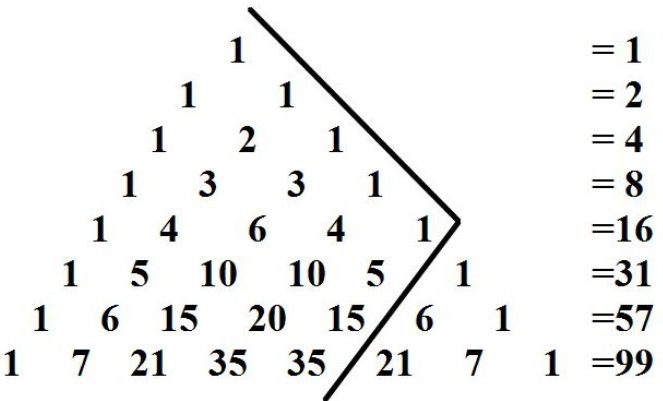
इससे पहले कि हम पता लगाने के लिए दिलचस्प गुणों के पास्कल त्रिभुज, अपनी पूर्णता में और सादगी के साथ, आपको पता होना चाहिए कि यह क्या है ।

वैज्ञानिक रूप से बोल रहा हूँ, इस संख्यात्मक योजना - अनंत तालिका आकार में त्रिकोणीय है, का गठन से binomial coefficients की व्यवस्था में एक विशेष आदेश है । अपने ऊपर और पक्षों संख्या रहे हैं 1. अन्य पदों की संख्या के बराबर करने के लिए दो संख्याओं का योग स्थित उनके ऊपर अगला ऊपर है । इस मामले में, सभी पंक्तियों के पास्कल त्रिकोण के सापेक्ष सममित है इसकी ऊर्ध्वाधर धुरी है ।

मुख्य गुण

पास्कल के त्रिभुज में हड़ताली है इसकी पूर्णता है । के लिए किसी भी पंक्ति संख्या n (n = 0, 1, 2…) यह सच है:

<उल>

पहली और आखिरी नंबर और mdash; 1;

दूसरे और अंत से पहले और mdash; एन;

तीसरे नंबर है, एक त्रिकोणीय संख्या (हलकों की संख्या कर सकते हैं कि व्यवस्था की जा के रूप में एक समबाहु त्रिकोण है, यानी, 1, 3, 6, 10): टी_{N-1 = n (n - 1) / 2.}

चौथे नंबर tetrahedral है, यानी यह एक पिरामिड के साथ एक त्रिकोण के आधार पर.

इसके अलावा, अपेक्षाकृत हाल ही में, 1972 में, यह पाया गया था की एक और संपत्ति पास्कल त्रिकोण है. आदेश में यह पता लगाने के लिए, आप की जरूरत है नीचे लिखने के लिए तत्वों की इस योजना के रूप में एक तालिका के साथ एक पंक्ति पारी में 2 पदों. तो चिह्नित कर रहे हैं कि संख्या के द्वारा विभाज्य पंक्ति संख्या है । यह पता चला है कि संख्या के स्तंभ चयनित संख्या एक प्रमुख संख्या है.

एक ही चाल कर सकते हैं किया जा सकता है अलग ढंग से. ऐसा करने के लिए, में पास्कल त्रिकोण की जगह पर संख्या के अवशेष उनके प्रभाग लाइन पर तालिका में नंबर. फिर एक लाइन में जिसके परिणामस्वरूप त्रिकोण इतना है कि अगले एक शुरू करने के लिए सही 2 कॉलम से पहला तत्व पिछले एक के. फिर स्तंभों है कि कर रहे हैं कि संख्या, प्रधानमंत्री संख्या, शामिल होंगे केवल शून्य है, और जो उन लोगों में मिश्रित कर रहे हैं शामिल होंगे कम से कम एक शून्य है ।

कनेक्शन के साथ द्विपद प्रमेय

के रूप में जाना जाता है, तथाकथित सूत्र के लिए अपघटन के मामले में पूरे गैर-नकारात्मक की डिग्री का योग दो चर है जो फार्म:

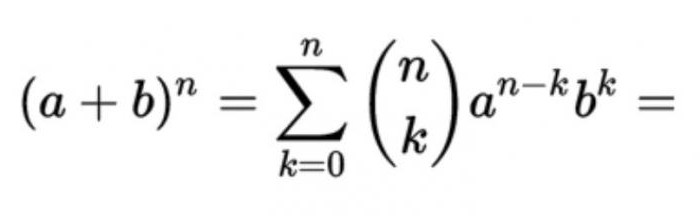
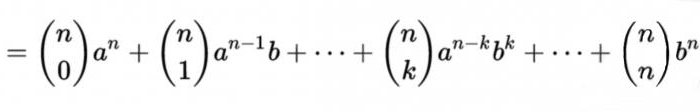
वर्तमान में उन्हें गुणांक कर रहे हैं सी करने के लिए बराबर है_{N^M = n! / (m! (n - m)!), जहां एम का प्रतिनिधित्व करता है, क्रमसूचक संख्या की एक पंक्ति में एन पास्कल त्रिभुज की है । दूसरे शब्दों में, इस तालिका में, आप आसानी से किसी भी बढ़ाकी संख्या पूर्व की व्यवस्था में उन्हें दो शर्तों.}

तो, पास्कल के त्रिभुज और द्विपद प्रमेय बारीकी से interrelated रहे हैं.

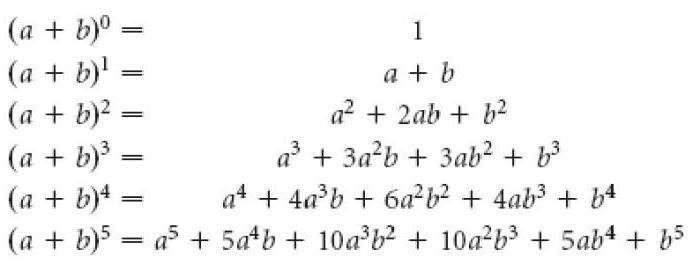
गणितीय चमत्कार

एक सावधान अध्ययन के पास्कल त्रिभुज, आप पा सकते हैं कि:

<उल>

सभी संख्याओं का योग में पंक्ति के साथ एक अनुक्रम संख्या n (0 से गिनती) 2 के बराबर है^N;

रेखा के लिए गठबंधन छोड़ दिया, तो रकम की संख्या के साथ विकर्णों के पास्कल त्रिकोण से जा रहा है, ऊपर से नीचे और बाएँ से सही करने के लिए, के बराबर फिबोनैकी संख्या;

पहली "विकर्ण" के होते हैं प्राकृतिक अनुक्रम में संख्या;

किसी भी मद से पास्कल त्रिभुज, कम प्रति यूनिट की राशि के बराबर सभी नंबरों के अंदर स्थित चतुर्भुज है जो से घिरा छोड़ दिया और सही विकर्ण पर एक दूसरे को काटना है कि यह संख्या;

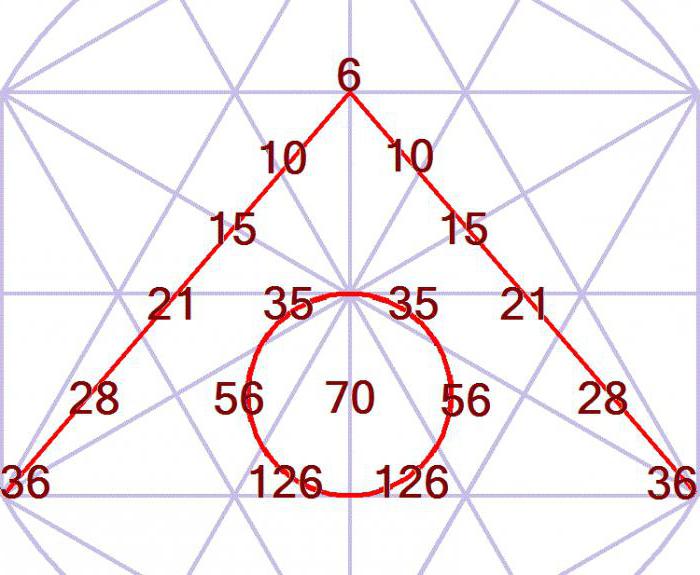
प्रत्येक पंक्ति में के आरेख का योग की संख्या में यहां तक कि स्थानों के बराबर की राशि के तत्वों पर अजीब स्थानों में.

Sierpinski त्रिकोण

इस तरह के दिलचस्प गणितीय योजना काफी होनहार देखने के बिंदु से की जटिल कार्यों को सुलझाने के लिए, यह बदल जाता है बाहर, अगर आप पेंट भी संख्या Paskaleva छवि में एक रंग है, और अजीब-दूसरे में.

Sierpinski त्रिकोण में स्थापित कर सकते हैं एक और तरीका है:

<उल><ली>में छायांकित चित्र के पास्कल एक अलग रंग में रंगना बीच त्रिकोण का गठन किया गया है जो जोड़ने के द्वारा midpoints के पक्ष में मूल;

इसी प्रकार, इस अधिनियम के तीन unpainted कोनों में स्थित है.

यदि प्रक्रिया अनिश्चित काल तक जारी रखा, परिणाम होना चाहिए दो टोन आंकड़ा है ।

सबसे दिलचस्प सुविधा के Sierpinski त्रिकोण और mdash; अपने स्व-समानता, के रूप में यह के होते हैं 3 प्रतियां कर रहे हैं कि 2 बार में कम हो. यह अनुमति देता है के लिए संबंधित करने के लिए इस योजना के भग्न घटता है, के रूप में वे शो के नवीनतम अनुसंधान के लिए सबसे उपयुक्त है गणितीय मॉडलिंग के बादल, पौधों, नदी डेल्टा, और ब्रह्मांड ही है ।

कुछ दिलचस्प चुनौतियों

जहाँ आप का उपयोग करें पास्कल त्रिभुज है? उदाहरण के कार्यों में हल किया जा सकता है के साथ, यह काफी विविध रहे हैं और करने के लिए संबंधित के विभिन्न क्षेत्रों में विज्ञान है. में से कुछ पर विचार उनमें से सबसे दिलचस्प है ।

1 समस्या है । कुछ बड़े शहर के दीवारों से घिरा हुआ है, केवल एक ही प्रवेश द्वार है । पहले चौराहे पर, मुख्य सड़क diverges दो. एक ही होता है किसी अन्य के साथ. जाने के लिए शहर के 210 लोगों को. पर प्रत्येक के आम चौराहों, वे कर रहे हैं, आधे में विभाजित किया गया है । कितने लोगों को आप पाते हैं हर चौराहे पर, जब साझा करने के लिए असंभव हो जाएगा. उसका जवाब है 10 पास्कल त्रिभुज की पंक्ति (गुणांक सूत्र प्रस्तुत किया इसके बाद के संस्करण), जहां पर दोनों पक्षों के ऊर्ध्वाधर अक्ष की संख्या 210 है ।

कार्य 2. वहाँ रहे हैं 7 प्रकार के रंग. आप की जरूरत है, एक गुलदस्ता बनाने के लिए 3 के फूल । आप चाहते हैं कि कैसे पता लगाने के लिए कई अलग अलग तरीकों से यह किया जा सकता है । इस समस्या के साहचर्य है. इसके समाधान के लिए, का उपयोग कर फिर से पास्कल त्रिकोण और एक 7 स्ट्रिंग तीसरे स्थान पर है (नंबरिंग में दोनों मामलों के साथ 0) संख्या 35.

अब आप जानते हैं कि द्वारा आविष्कार किया गया था महान फ्रांसीसी दार्शनिक और वैज्ञानिक ब्लेज पास्कल. अपने प्रसिद्ध त्रिकोण, जब ठीक से इस्तेमाल किया जा सकता है एक असली lifesaver कई कार्यों के लिए, विशेष रूप से के क्षेत्र में साहचर्य है. इसके अलावा, यह संभव है का उपयोग करने के लिए हल करने के लिए कई रहस्यों के साथ जुड़े भग्न है.