Now - 02:19:11
Trójkąt Pascala. Właściwości trójkąta Pascala
Postęp ludzkości w dużej mierze jest związana z odkryciami, wykonanymi geniuszy. Jednym z nich jest Blaise Pascal. Jego biografia twórcza jeszcze raz potwierdza prawdziwość wyrażenia Lyonu Фейхтвангера «Utalentowany człowiek, utalentowany we wszystkich». Wszystkie naukowe osiągnięcia tego wielkiego uczonego trudno zliczyć. Do ich grona należy jeden z najbardziej eleganckich wynalazków w świecie matematyki ó trójkąt Pascala.

Kilka słów o geniuszu
Blaise Pascal według nowoczesnych standardów, zmarł wcześnie, w wieku 39 lat. Jednak redakcjo, wykazał się jako wybitny fizyk, matematyk, filozof i pisarz. Wdzięczni potomni nazwali na jego cześć jednostkę ciśnienia i popularny język programowania Pascal. On już prawie 60 lat służy do nauki pisania różnych kodów. Na przykład, z jego pomocą każdy uczeń może napisać program do obliczania powierzchni trójkąta na «Pascalu», a także zbadać właściwości schematu, o którym mowa poniżej.
Działalność tego naukowca z niezwykłym podejściem obejmuje różne dziedziny nauki. W szczególności, Blaise Pascal jest jednym z założycieli hydrostatyki analizy matematycznej, niektórych kierunków geometrii i teorii prawdopodobieństwa. Ponadto, jest:
- Stworzył mechaniczny kalkulator, znany pod nazwą Paskaleva koła;
- Wprowadziła eksperymentalny dowód na to, że powietrze ma jędrności i ma ciężar;
- Stwierdził, że barometr można użyć do przewidywania pogody;
- Wynalazł samochód;
- Wymyślił omnibus ó bryczką ze stałymi trasami, które stały się później pierwszym widokiem regularnego transportu publicznego, itp.
Arytmetycznych trójkąt Pascala
Jak już wspomniano, ten wielki francuski naukowiec wniósł ogromny wkład w naukę matematyki. Jednym z jego niezaprzeczalne naukowych dzieł jest «Traktat o арифметическом trójkącie», który składa się z биномиальных współczynników, ułożone w określonym porządku. Właściwości tego schematu zadziwiają swoją różnorodnością, a ona sama potwierdza przysłowie «Wszystko genialne ó w!».
Bardziej:
Główne etapy rozwoju psychiki w филогенезе
Rozwój psychiki w филогенезе charakteryzuje się kilkoma etapami. Rozważmy dwie główne historie związane z tym procesem.Филогенез - to historyczny rozwój, obejmującego miliony lat ewolucji, historię rozwoju różnych gatunków organizmów żywych.Ontogenez...
Co to jest gronkowiec i metody jego leczenia
Wielu w swoim życiu miał do czynienia z zakażeniem gronkowca. Dlatego konieczne jest posiadanie pełnej informacji o tej chorobie, aby w pełni zrozumieć, co dzieje się w organizmie. Więc co to jest gronkowiec? To bakterie, lub jedną z ich odmian, z kt...
Przed podjęciem się, że studiuje morfologia, należy zauważyć, że sam studiuje ten dział gramatyki. Tak, morfologia studiuje słowo jako część mowy, a także sposoby jego edukacji, jego formy, struktury i gramatyki wartości, a także poszczególne j...
Trochę historii
Dla Sprawiedliwości trzeba powiedzieć, że właściwie trójkąt Pascala był znany w Europie jeszcze w początku 16 wieku. W szczególności, jego obraz można zobaczyć na okładce podręcznika arytmetyki słynnego astronoma Piotra Апиана z Ингольтштадского uniwersytetu. Podobny trójkąt przedstawiony jako ilustracja w książce chińskiego matematyka Yang Hui, wydanej w roku 1303. O jego właściwościach wiadomo było również i wspaniałej perskiego poety i filozofa Omar Хайяму jeszcze na początku 12 wieku. Przy czym uważa się, że spotkał się z nim z traktatów arabskich i indyjskich naukowców, napisanych wcześniej.
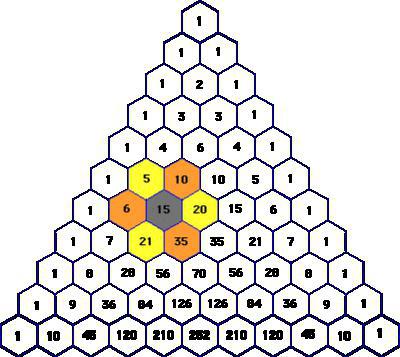
Opis
Zanim odkryć ciekawe właściwości trójkąta Pascala, pięknego w swej doskonałości i prostoty, warto dowiedzieć się, co to jest.
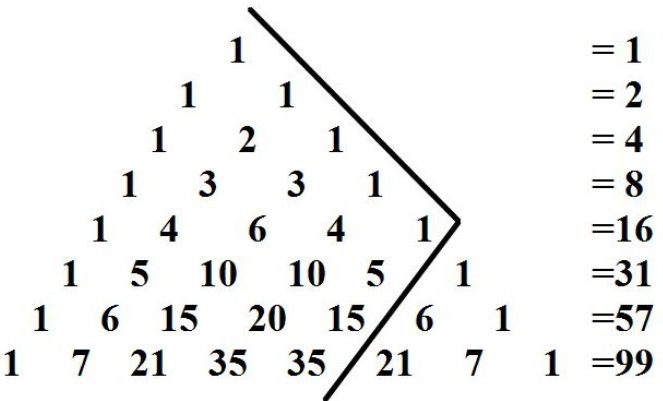
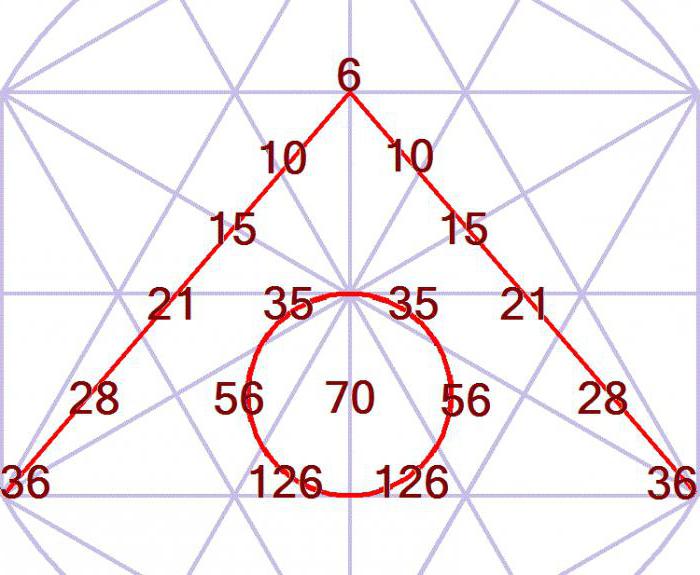
Mówiąc naukowym językiem, ta wartość liczbowa schemat - nieskończona tabela trójkątny kształt, utworzona z биномиальных współczynników znajdujących się w określonej kolejności. W jego szczycie i po bokach znajdują się cyfry 1. Pozostałe pozycje zajmują liczby równe sumy dwóch liczb znajdujących się nad nimi, obok wyżej. Przy tym wszystkie wiersze trójkąta Pascala są symetryczne względem osi pionowej.
Podstawowe właściwości
Trójkąt Pascala zachwyca doskonałością. Dla każdego wiersza o numerze n (n = 0, 1, 2…) prawda:
- Pierwszy i ostatni numer ó 1;
- Drugi i przedostatni ó n;
- Trzecia liczba jest równa треугольному liczby (ilości kółek, które można umieścić w formie trójkąta równobocznego, czyli 1, 3, 6, 10): TNO-1 = n (n - 1) / 2.
- Czwarta liczba jest тетраэдрическим, tj. przedstawia piramidę z trójkąta w podstawie.
Ponadto, stosunkowo niedawno, w 1972 roku, stwierdzono jeszcze jedną właściwość trójkąta Pascala. Aby go odkryć, trzeba nagrać elementy tego schematu w postaci tabeli z przesunięciem linii na 2 pozycji. Następnie podkreślają liczby, dzieli się na numer wiersza. Okazuje się, że numer kolumny, w której wyróżnione wszystkich liczb, jest liczbą pierwszą.
Ten sam trik można wykonać w inny sposób. Do tego w trójkącie Pascala zastępują liczby na resztki z ich podziału na numer wiersza w tabeli. Następnie dysponują wiersza w powstałym trójkącie tak, aby następna z nich rozpoczęła się w prawo na 2 kolumny od pierwszego elementu poprzedniej. To kolumny, które mają numery, które są liczbami pierwszymi, będą składać się tylko z zer, a w tych, które są złożone, będzie obecny przynajmniej jeden zero.
Komunikacja z биномом Newtona
Jak wiadomo, tak nazywa się formuła dla rozkładu względem całej неотрицательной stopniu sumy dwóch zmiennych, która ma postać:
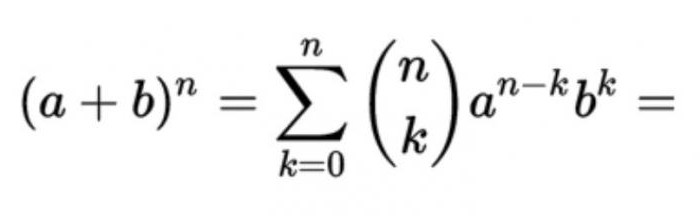
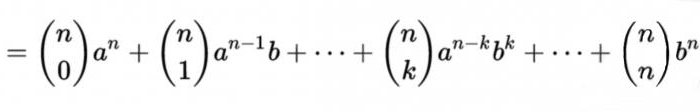
Obecni w nich współczynniki są równe CNM = n! / (m! (n - m)!), gdzie m, stanowi numer porządkowy liczby w wierszu n trójkąta Pascala. Innymi słowy, mając pod ręką tę tabelę, można łatwo budować w stopień wszelkieliczby, wstępnie rozszerzenie ich na dwie części składowe.
W Ten sposób, trójkąt Pascala i fasoli Newtona są ze sobą wzajemnie powiązane jest najściślej.
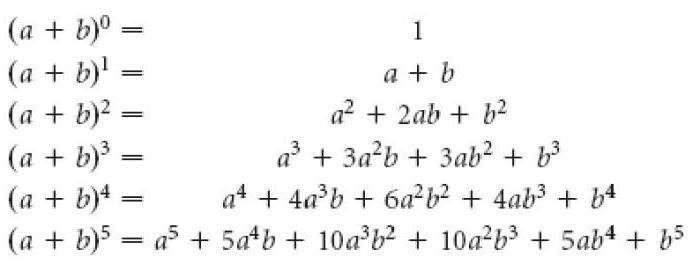
Matematyczne cuda
Przy pilnej nauce trójkąta Pascala można wykryć, że:
- Suma wszystkich liczb w wierszu o numerze n (licząc od 0) jest równa 2N;
- Jeśli polecenia wyrównaj do lewej, to suma liczb, które znajdują się wzdłuż przekątnych w trójkącie Pascala, idących z dołu do góry i od lewej do prawej, są równe liczb Fibonacciego;
- Pierwsza «przekątna» składa się z liczb naturalnych, idących po kolei;
- Każdy element z trójkąta Pascala, obniżony na jednostkę, jest równy sumie wszystkich liczb znajdujących się wewnątrz równoległoboku, który jest ograniczony lewymi i prawymi przekątnych, przecinających się na tym;
- W każdym wierszu schematu suma cyfr na miejscach parzystych jest równa sumie elementów na nieparzystych miejscach.
Trójkąt Sierpińskiego
Taka ciekawa matematyczny schemat, tyle obiecujące z punktu widzenia rozwiązywania złożonych zadań, okazuje się, że jeśli pokolorować liczb parzystych Паскалевого obrazu w jednym kolorze, a odd ó w drugiej.
Trójkąt Sierpińskiego można zbudować i w inny sposób:
- W cieniowanego schemacie Pascala przemalować na inny kolor oś trójkąt, który powstał przez połączenie sposobów stron źródłowego;
- Dokładnie pochodzi również z trzema незакрашенными, zlokalizowanych w narożnikach;
- Jeśli proces nie ma końca, to w końcu musi się udać bicolor postać.
Najciekawsze jest to właściwość trójkąta Sierpińskiego ó jego самоподобие, ponieważ składa się z 3-ch swoich kopii, które zmniejszono 2 razy. To pozwala zaliczyć ten schemat do фрактальным krzywą, a oni, jak pokazują najnowsze badania najlepiej nadają się do modelowania matematycznego chmur, roślin, delty rzek, tak i Wszechświat.
Kilka ciekawych zadań
Gdzie jest trójkąt Pascala? Przykłady zadań, które można rozwiązać z jego pomocą, są dość zróżnicowane i należą do różnych obszarów nauki. Rozważmy niektóre, najbardziej interesujące z nich.
Zadanie 1. U pewnego dużego miasta, обнесенного murem, tylko jedna brama wjazdowa. Na pierwszym skrzyżowaniu podstawowe droga rozdwaja się na dwie. To samo dzieje się na każdym innym. Do miasta wchodza 210 osób. Na każdym z napotkanych skrzyżowań są one podzielone na pół. Ile osób będzie znajdować się na każdym skrzyżowaniu, kiedy dzielić będzie już niemożliwe. Jej odpowiedzią jest 10 wiersz trójkąta Pascala (formuła kursów przedstawiony powyżej), gdzie po obu stronach od osi pionowej znajdują się liczby 210.
Zadanie 2. Istnieje 7 rodzajów kolorów. Trzeba zrobić bukiet z 3 kwiatów. Chcesz dowiedzieć się, ile różnych sposobów można to zrobić. To zadanie z zakresu комбинаторики. Do jej rozwiązania ponownie korzystamy z trójkąta Pascala i otrzymujemy na 7 linii na trzeciej pozycji (numeracja w obu przypadkach z 0) liczba 35.

Teraz już wiesz, że wynalazł wielki francuski filozof i uczony Blaise Pascal. Jego słynny trójkąt przy odpowiednim wykorzystaniu mogą stać się prawdziwe wybawienie dla rozwiązania wielu zadań, zwłaszcza z zakresu комбинаторики. Ponadto, można użyć do rozwiązywania licznych zagadek, związanych z fraktalami.
Article in other languages:
AR: https://tostpost.com/ar/education/129-pascal-s-triangle-properties-of-pascal-s-triangle.html
BE: https://tostpost.com/be/adukacyya/218-trohkutn-k-paskalya-lasc-vasc-trykutn-ka-paskalya.html
En: https://tostpost.com/education/387-pascal-s-triangle-properties-of-pascal-s-triangle.html
HI: https://tostpost.com/hi/education/129-pascal-s-triangle-properties-of-pascal-s-triangle.html
JA: https://tostpost.com/ja/education/128-pascal-s-triangle-properties-of-pascal-s-triangle.html
KK: https://tostpost.com/kk/b-l-m/218-shb-rysh-paskal-asietter-shb-rysh-paskal.html
PT: https://tostpost.com/pt/educa-o/218-tri-ngulo-de-pascal-propriedades-do-tri-ngulo-de-pascal.html
TR: https://tostpost.com/tr/e-itim/224-gen-pascal-pascal-geni-zellikleri.html
UK: https://tostpost.com/uk/osv-ta/220-trikutnik-paskalya-vlastivost-trikutnika-paskalya.html
ZH: https://tostpost.com/zh/education/145-pascal-pascal.html

Alin Trodden - autor artykułu, redaktor
"Cześć, jestem Alin Trodden. Piszę teksty, czytam książki, Szukam wrażeń. I nie jestem zły w opowiadaniu ci o tym. Zawsze chętnie biorę udział w ciekawych projektach."
Nowości
co roku 14 lipca francuzi obchodzą Dzień Bastylii. Święto bardzo specyficzny i dość nieoczekiwany. I aby zorientować się, z czym to jest związane, potrzebny jest mała historia. Potężna twierdza, z wysokimi murami i ośmioma wieżami...
Początki historycznego mitu, lub do czego wikingowie rogaty hełm
Do czego wikingowie rogaty hełm? Nowoczesne obrazy często przedstawiają tych średniowiecznych wojowników groźni i rozpaczliwe zawodnikami z imponującej wielkości topory i wciągającej zbroi. Ale dlaczego wikingowie rogaty hełm? Prz...
Błędy w użyciu czasownika "zwracać się" - to wynik błędnej interpretacji słowa
Czasownik «zwracać się» - została zapożyczona z języka obcego słowa. Prawdopodobnie, dlatego jego stosowanie wiąże się z częstym mowy błędem.Pochodzenie słowaSłowo «zwracać się» pochodzi od łacińskiego appe...
Dzieci Katarzyny Wielkiej. Zarząd i osobiste życie Katarzyny Wielkiej
Rosyjska cesarzowa Katarzyna ii, znana również jako Wielka, panowała z 1762 roku w 1796-th. Swoje wysiłki ona znacznie rozszerzył imperium, znacznie poprawiła systemu zarządzania i energicznie prowadziła politykę zachodnią, подраз...
Sztuka i nauka. Działacze nauki i sztuki
Jeśli spojrzeć na sposób, który przeszedł ludzkość, można mówić o tym, że dla przedstawiciela homo sapiens głównymi zawsze były trzy zadania: przetrwać, uczyć się i tworzyć. Jeśli w odniesieniu do pierwszej kwestii nie występuje w...
Vicomte - to... Pochodzenie tytułu
Średniowieczna szlachecki hierarchia pozostaje dla wielu naszych współczesnych trudne i kłopotliwe. Nie ma w tym nic dziwnego, ponieważ nawet wśród współczesnych szlacheckiej szlachta często występowały różnice w znaczeniu i solid...






















Uwaga (0)
Ten artykuł nie ma komentarzy, bądź pierwszy!