Now - 02:07:50
Pascal's Triangle. Properties of Pascal's triangle
Human Progress is largely due to the discoveries made by geniuses. One of them is Blaise Pascal. His biography confirms the truth of the expression lion Feuchtwanger “a Talented person is talented in everything”. All the scientific achievements of this great scientist it is difficult to enumerate. Among them is one of the most elegant inventions in the world of mathematics-Pascal's triangle.

A Few words about the genius
Blaise Pascal by modern standards, he died early, at the age of 39 years. However, in his short life he proved himself as an outstanding physicist, mathematician, philosopher, and writer. Grateful descendants named in his honor the unit of pressure and popular Pascal programming language. He was almost 60 years old used to teach the writing of different codes. For example, with his help, every student can write a program to compute the area of a triangle on the "Pascal", as well as to explore the properties of the scheme, which will be discussed below.
The Activities of this scientist with extraordinary thinking covers very diverse areas of science. In particular, Blaise Pascal is one of the founders of hydrostatics mathematical analysis, several areas of geometry and probability theory. In addition, he:
- Created a mechanical calculator, known as Paskaleva wheel;
- Presented experimental proof that air has elasticity and has a weight;
- Found that the barometer can be used to predict the weather;
- Invented the wheelbarrow;
- Invented omnibus — the horse-drawn carriages with fixed routes, who later became the first regular public transport, etc.
Arithmetic Pascal's triangle
As has been said, this great French scientist has made an enormous contribution to mathematical science. One of his absolute masterpieces of science is “Treatise on the arithmetical triangle", which consists of the binomial coefficients arranged in a particular order. The properties of this scheme are astonishingly varied, and she confirms the adage “All brilliant — simple!”.
Recommended
"Knowledge is light and ignorance is darkness": the value, meaning and alternatives
There are some sayings that would seem to need no explanation, such as “teaching & ndash; light and ignorance – darkness”. But some still do not understand their meaning. But not only for such people is written by our article. I...
What was invented by Mendeleev for the army. The history and fate of the invention
D. I. Mendeleev was a brilliant Russian scientist-polymath, who made many important discoveries in various fields of science and technology. Many people know that he is the author of “Fundamentals of chemistry" and the periodic law of chem...
The origin of the Slavs. The influence of different cultures
Slavs (under this name), according to some researchers, appeared in the story only in 6 century ad. However, the language of nationality bears the archaic features of the Indo-European community. This, in turn, suggests that the origin of the Slavs h...
A Little history
In Fairness I must say that in fact Pascal's triangle was known in Europe in the early 16th century. In particular, its image can be seen on the cover of textbook arithmetic, the famous astronomer Peter Apian from Ingoldstadt University. Similar triangle presented as illustrations in the book by the Chinese mathematician Yang Hui, published in 1303. His properties were known also a great Persian poet and philosopher Omar Khayyam in the early 12th century. Moreover, it is believed that he was acquainted with him from treatises Arabic and Indian scholars written.
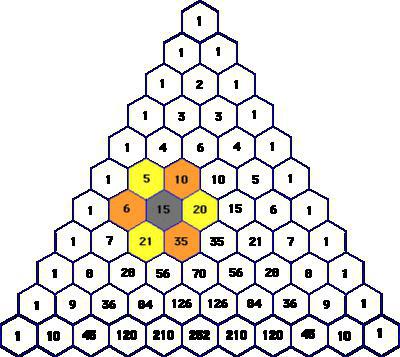
Description
Before we explore the interesting properties of Pascal's triangle, beautiful in its perfection and simplicity, you should know what it is.
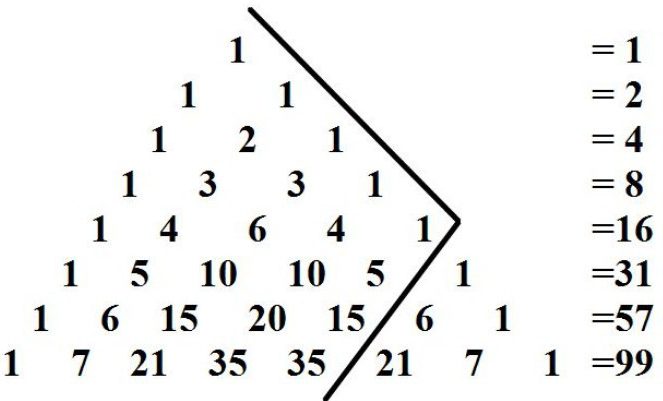
Scientifically Speaking, this numerical scheme - the infinite table is triangular in shape, formed from the binomial coefficients arranged in a particular order. In its top and sides are numbers 1. Other positions is the number equal to the sum of the two numbers located above them next above. In this case, all the rows of Pascal's triangle is symmetrical relative to its vertical axis.
Main properties
Pascal's Triangle is striking in its perfection. For any row number n (n = 0, 1, 2…) true:
- The first and last numbers — 1;
- The second and penultimate — n;
- The third number is a triangular number (the number of circles that can be arranged in the form of an equilateral triangle, i.e., 1, 3, 6, 10): TN-1 = n (n - 1) / 2.
- The fourth number is tetrahedral, i.e. it is a pyramid with a triangle at the base.
In addition, relatively recently, in 1972, it was found another property of Pascal's triangle. In order to detect it, you need to write down the elements of this scheme in the form of a table with a row shift by 2 positions. Then mark the numbers that are divisible by the row number. It turns out that the number of the column where the selected number is a Prime number.
The same trick can be done differently. To do this in the Pascal triangle replace the numbers on the remnants of their division on the line number in the table. Then have a line in the resulting triangle so that the next one started to the right 2 columns from the first element of the previous one. Then columns that have numbers that are Prime numbers, will consist only of zeros, and in those who are composite will contain at least one zero.
The connection with the binomial theorem
As is known, the so-called formula for the decomposition in terms of the whole non-negative degrees of sum of two variables which has the form:
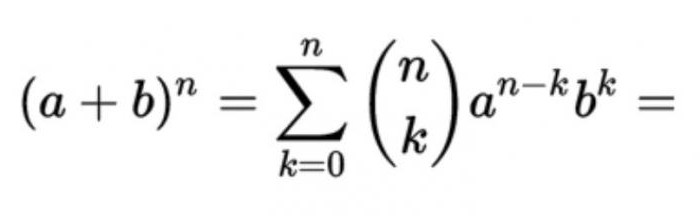
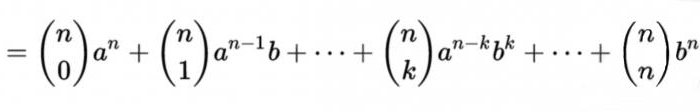
Present in them the coefficients are equal to CNM = n! / (m! (n - m)!), where m represents the ordinal number of numbers in row n of Pascal's triangle. In other words, with this table, it's easy to raise any number of pre-arranging them into two terms.
So, Pascal's triangle and the binomial theorem are interrelated closely.
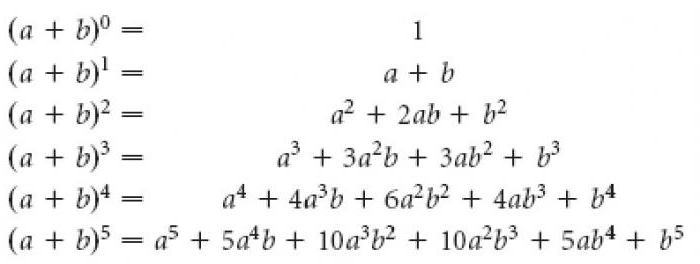
Mathematical miracles
A careful study of Pascal's triangle, you may find that:
- The sum of all numbers in the row with a sequence number n (counting from 0) is equal to 2N;
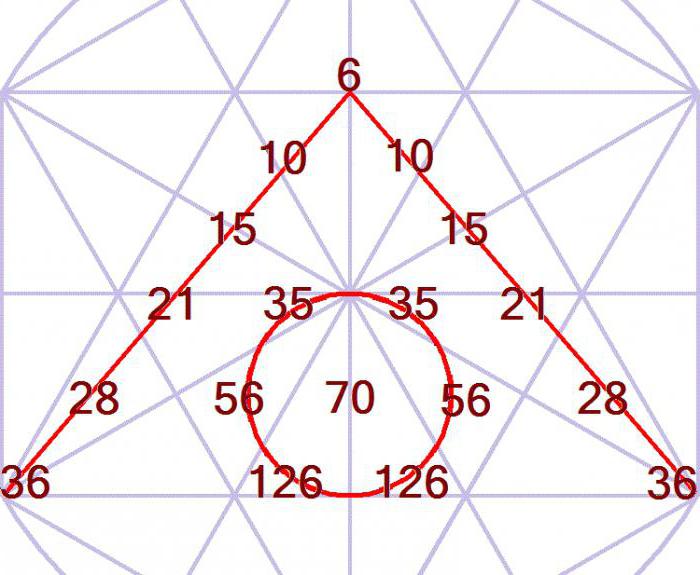
- Line aligned to the left, then the sums of the numbers along the diagonals of Pascal's triangle, going from the bottom up and from left to right, equal to the Fibonacci numbers;
- The first "diagonal" consists of the natural numbers in sequence;
- Any item from the Pascal's triangle, reduced per unit equal to the sum of all the numbers located inside the parallelogram which is bounded by left and right diagonals that intersect at this number;
- In each row of the diagram the sum of the numbers in even places equals the sum of elements at odd places.
Sierpinski Triangle
Such interesting mathematical scheme is quite promising from the point of view of solving complex tasks, it turns out, if you paint even numbers Paskaleva image in one color, and odd-in another.
Sierpinski Triangle can be set up in another way:
- In the shaded diagram of Pascal repaint in a different color the middle triangle, which is formed by connecting the midpoints of the sides of the original;
- Similarly, the act of three unpainted located in the corners.
- If the procedure is continued indefinitely, the result must be two-tone figure.
The Most interesting feature of the Sierpinski triangle — its self-similarity, as it consists of 3 copies that are reduced in 2 times. It allows to relate this scheme to the fractal curves, as they show the latest research is best suited for the mathematical modeling of clouds, plants, river deltas, and the Universe itself.
Some interesting challenges
Where you use the Pascal's triangle? Examples of tasks that can be solved with it, are quite diverse and belong to different fields of science. Consider some of the most interesting of them.
Problem 1. Some of the big city, surrounded by walls, only one entrance gate. At the first intersection, the main road diverges into two. The same happens with any other. Go to the city of 210 people. On each of the common intersections, they are divided in half. How many people will you find at each intersection, when to share will be impossible. Her answer is 10 row of Pascal's triangle (formula coefficients presented above), where on both sides of the vertical axis are the number 210.
Task 2. There are 7 kinds colors. You need to make a bouquet of 3 flowers. You want to find out how many different ways it can be done. This problem of combinatorics. For its solution, again using Pascal's triangle and get a 7 string on the third position (numbering in both cases with 0) number 35.

Now you know that was invented by the great French philosopher and scientist Blaise Pascal. His famous triangle, when used properly, can be a real lifesaver for many tasks, especially in the field of combinatorics. In addition, it is possible to use for solving the many mysteries associated with fractals.
...Article in other languages:
AR: https://tostpost.com/ar/education/129-pascal-s-triangle-properties-of-pascal-s-triangle.html
BE: https://tostpost.com/be/adukacyya/218-trohkutn-k-paskalya-lasc-vasc-trykutn-ka-paskalya.html
HI: https://tostpost.com/hi/education/129-pascal-s-triangle-properties-of-pascal-s-triangle.html
JA: https://tostpost.com/ja/education/128-pascal-s-triangle-properties-of-pascal-s-triangle.html
KK: https://tostpost.com/kk/b-l-m/218-shb-rysh-paskal-asietter-shb-rysh-paskal.html
PL: https://tostpost.com/pl/edukacja/221-tr-jk-t-pascala-w-a-ciwo-ci-tr-jk-ta-pascala.html
PT: https://tostpost.com/pt/educa-o/218-tri-ngulo-de-pascal-propriedades-do-tri-ngulo-de-pascal.html
TR: https://tostpost.com/tr/e-itim/224-gen-pascal-pascal-geni-zellikleri.html
UK: https://tostpost.com/uk/osv-ta/220-trikutnik-paskalya-vlastivost-trikutnika-paskalya.html
ZH: https://tostpost.com/zh/education/145-pascal-pascal.html

Alin Trodden - author of the article, editor
"Hi, I'm Alin Trodden. I write texts, read books, and look for impressions. And I'm not bad at telling you about it. I am always happy to participate in interesting projects."
Related News
The biggest island of the Earth: descriptions
Before we talk about what the biggest island of the Earth, it should be understood that generally is an island. Some, when they hear the word, picture the images of resort areas, for example, Crete, the Maldives, Sicily, others im...
The common amoeba, its habitat, features of the structure and functioning of
the common Amoeba apparently a cell is directly related to the type of protozoa, class of corneous, or even call them Sarkodie. They have pseudopods, which are the organs by which they move and capture food. Dense shell at the c...
Should I write the diploma itself?
Every student in the process of learning wants to study, get a diploma and find a job in his field. And that's when the last final phase of learning, namely, submission of the thesis is not far off many students for a variety of r...
The unit of density of the substance
What is the unit of density? Find out the features of this physical quantity.This term is an important indicator of oil and various petroleum products.termIn the modern petrochemical use such units of density as kg/m3 and g/m3. Wi...
The popular movement in the 17th century
the popular movement in the 17th century in Russia was a mass phenomena. The time of Troubles ended. All spheres of public life was completely destroyed: economy, politics, social relations, culture, spiritual development. Natural...
Intuition - what is it? The meaning and interpretation of
any person, probably, there were moments of sudden insight, when he didn't know how to do it properly, but in the end worked perfectly. Today we will discuss such behavior in the context of our theme. Consider such a thing as "int...






















Comments (0)
This article has no comment, be the first!