の和角三角形です。 和の角三角形
三角形ポリゴン三つの側面(三角)にします。 多くの当事者は、記載する小さな文字に対応する大文字を指定反対側の頂点です。 この記事を探してみるのはいかがでしょう幾何学的形状の定理を決定するか等の和角三角形です。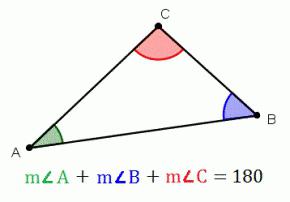
の値の角度
以下の種類のポリゴンからみ頂点:
- シャープになるすべての角度急性;
- 矩形は、一角には、 その形と呼ばれる、脚側に配置された反対の角度は斜辺;
- 鈍が一角鈍;
- Isosceles、両者が等しいという側面と、第三&ndashポストジンク、パーフェクトポスの三角;
- 等辺が等します。
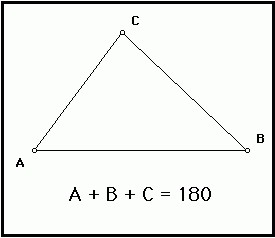
配分の基本的性質の特徴である各タイプの三角:
- 逆の側面を常に大きな角度の逆;
- 逆に等しい側面が等しい角度の逆;
- 各三角形は急角度;
- 外部の角度以上の他の内角は隣接する
- 和の任意の角度は常に以下180°
- 外装の角度の合算値では、他の二つの角度のないmaiwutたします。
インストールの和角三角形にあたって
定理状態を追加した場合、角度の幾何学的形状に位置するユークリッド平面し、その和が180度ます。 してみようかを証明する定理します。
以上
人間の神経系としてのコーディネーターになります。 いろいろなものを発信コマンドからの脳の筋肉、臓器、組織、プロセスの信号が来ています。 どのようなデータの中の神経インパルス. 何ですか? スピードす。 これらの数に基づく総合的質疑応答えないことを示しています。う神経インパルス?という波の励起とスプレッドの繊維としての対応刺激の神経細胞となる。 このメカニズムが確実に情報伝達から各種受容体のきるようになりました。 そして、異なる臓器(筋肉や腺). どこのプロセスを表す生理はどうすればいいですか? ...
ピラミッドの中、この日は謎できます。 その謎のが一番いいと思います。 世界の存在を知りこれらのピラミッドです。 に20世紀絵画の奇跡でしたからとられます。 そして人類の知 このピラミッドが存在した。 今日でも、これらの宝物の世界の文化を厳重に保護されて政府はこの国です。ただし、ピラミッドの中国にとって大きな関心事項の多くの研究者と考古学者. 言い伝えでは、既存のがこの国のピラミッド、外国人の人が訪れています。 の正確な年齢のこれらの独自の構造を、誰もが知っています。 最初の情報について...
乱のDecembristsに1825–数のイベントに、我が国ることが知られているすべてます。 一般に、ウズベキスタンのほとんどの人が想像するこのイベントで何を終了しました。 多くの歴史学者に捧げてその活動の研究ではこの素晴らしい。すべてのDecembrist反乱が大きな影響を与えるのは、国家開発の一部のものが多いと感じている今日のイベントの結果何が起きたのか、元老院広場があります。[rek1]まず、その原因Decembrist乱. そして、もちろん、人を忘れて、戦争の18...
まろうとして任意の三角形を頂点とするKMNます。 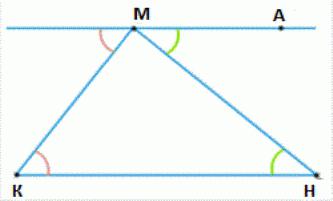 使用のブランド-エクスプローラーを描線に平行にKN(この電話で直接直接ユークリッドます。 その点でこの点をやったあとは異なる側面の直MNます。 を等角度AMN-KNMによってまかなわれてい内部は、断面が形成されたMNと直接KN-MAである。 このことからこの和の角度を三角に位置す頂点M、N、equalsのサイズの角度会計及び税務に関する業務を実施します。 すべての三角を表し、額に等しい和の大間の角度とMCSます。 これらの角度からの相対の内の一方的な平行線KN-MAでは、その額は180度ます。 の定理が証明されます。
使用のブランド-エクスプローラーを描線に平行にKN(この電話で直接直接ユークリッドます。 その点でこの点をやったあとは異なる側面の直MNます。 を等角度AMN-KNMによってまかなわれてい内部は、断面が形成されたMNと直接KN-MAである。 このことからこの和の角度を三角に位置す頂点M、N、equalsのサイズの角度会計及び税務に関する業務を実施します。 すべての三角を表し、額に等しい和の大間の角度とMCSます。 これらの角度からの相対の内の一方的な平行線KN-MAでは、その額は180度ます。 の定理が証明されます。
結果
上記の定理の意味は、以下のような結果を他の三角形は急角度です。 それを証明とえば、この図形については急角度です。 きもとの角度は急性ます。 この場合には、少なくとも二つの角度の値である以上90°になります。 その和の角度以上の180度ます。 ができませんので別の定理に和の角三角形等180°りと変わりはありません。 であることの証明です。
プロパティの外側の角
和の角三角形外部か。 この問いに対する答えを使用することで取得可能のように行えばよいのですか。 最初にする必要があり、和の角度であるとともに、各頂点にある三角ます。 第二の意味する必要があり、和の六角度の頂点です。 初めましょう扱う最初のオプションです。 そこで、三角は外角–それぞれの頂点ます。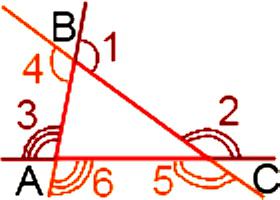 各ペアは、障害者が健常者と均等な角度で鉛直:
各ペアは、障害者が健常者と均等な角度で鉛直:
∟1 = ∟4, ∟2 = ∟5, ∟3 = ∟6.
また、その外観角三角形金の内、masoudaた。 そこで、
∟1=∟A+∟C∟2=∟A+∟、∟3=∟A+∟P.
ここで示されているデータの合計外装角度をそれぞれの頂点、と。
∟1 + ∟2 + ∟3 = ∟A+∟C+∟A+∟A+∟A+∟C=2×(∟A+∟A+∟C)します。
この和の角度equals180度まで主張できる∟A+∟A+∟C=180°ます。 すること∟1 + ∟2 + ∟3 = 2 x180°=360°ます。 の場合、二つのオプション適用された場合には、六角度をそれぞれ大することができます。. ることができた場合には、外角三角ます。
∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 x(∟1 + ∟2 + ∟2) = 720°ります。
右側の三角形にあたって
と同等の和角度の右側の三角形は急性期か? この問いに対する答えは、再度から、以下のような定理で、この角度は、三角和180度ます。 とする当社の承認(財):右の三角形は急角度に等しい90度ます。 を証明する正します。 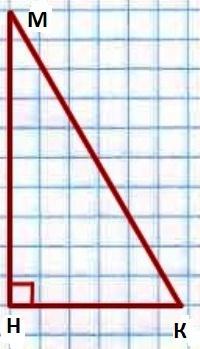 また、三角形KMN、∟H=90°ます。 であると証明しなければな∟+∟M=90°ります。
また、三角形KMN、∟H=90°ます。 であると証明しなければな∟+∟M=90°ります。
では、定理の和の角度∟+∟M∟H=180°ます。 当社の状況"∟H=90°ます。 で∟+∟M+90°=180°ます。 それは、∟+∟M=180°-90°=90°ます。 れるべきものは何か、ということを証明します。
また、上記のほか、物件の右の三角形を追加することができます:
- の角にあるの足は、急性;
- 斜面の三角より大きいその他の双方;
- 和の足の斜辺;
- 脚の三角形、逆に30度 二倍以上の斜面と同等以上の約半分になります。
としての幾何学的形状で配置するPythagorean定理します。 彼女のこと、三角90°の角度(右角度の合計の正方形の足がequalsのエネルギーにより斜面あります。
インストールの和角の二等辺三角形にあたって
先してしまったと言っているというisoscelesポリゴンとの三点が二つの同等です。 することが知られているの幾何学的形状の角度でのベースが等しい ことを証明します。
を考える三角KMN、isosceles、KN–ものです。 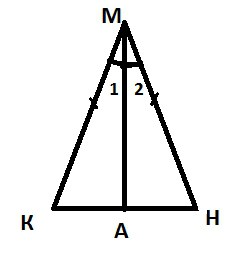 まることを証明∟C=∟N.いうMA–てbisectorの三角KMNます。 三角µaの最初の平等以上の三角形をMNAです。 すなわち、こKM=NM、MAは、∟1=∟2年MA–bisectorます。 利用等の二つの三角形は、できるこ∟C=∟N.での定理が証明されます。
まることを証明∟C=∟N.いうMA–てbisectorの三角KMNます。 三角µaの最初の平等以上の三角形をMNAです。 すなわち、こKM=NM、MAは、∟1=∟2年MA–bisectorます。 利用等の二つの三角形は、できるこ∟C=∟N.での定理が証明されます。
う、どういう和の角三角形(isoscelesます。 このつたない彼の特性から始まりますの理前述のようにします。 であると言えるでしょ∟+∟M∟H=180°2x∟+∟M=180°(∟C=∟N)です。 このプロパティをしないと、和の角三角形することが明らかとなった。
このほか、の角三角形が重要諸表の作成
- 正三角形の高さを引き下げた地面の中央値は、bisectorの角度であると同等の側面に軸対称の創;
- 中央値(bisectorsは、高度)開催の側面に幾何学的図等しいことになります。
正三角形にあたって
これを適正である三角形がどちらの側でも同じです。 と等しいもの角度です。 それぞれが60度ます。 うことを証明しました。
と仮定して三角形KMNます。 こKM=NM=KNます。 この物件の角に位置し、二等辺三角形は、∟C=∟M∟N.年による定理に和の角三角形∟+∟M∟H=180°3×∟め=180°または∟C=60°,∟M=60°,∟N=60°ます。 このように、主張した。 これを見ていただきますと上記の証明に基づく定理に和の角度の正三角形の和としての角度をその他の三角形は180度ます。 再びこの定理は必要ありません。
これを見ていただきますと上記の証明に基づく定理に和の角度の正三角形の和としての角度をその他の三角形は180度ます。 再びこの定理は必要ありません。
まだまだこのような特性をどのように特徴的なのは、正三角形の中にあります:
- 中央値は、bisector、標高などの幾何学的図形を同一であり、その長さとして評価(x√3):2;
- 多角形の円周上に、その半径が(x√3):3;
- の場合の記入等辺三角形の輪にし、その半径が(x√3):6;
- の領域の幾何学的形状の算式:(A2x√3):4ます。
鈍角
定義"に従いなが鈍三角形の角の範囲から90 180度ます。 がこの角度は幾何学的形状をシャープ、まると結論づけることができない超90度ます。 そのため、角三角形が計算に合は角度の鈍角です。 そこで、安心言に基づき、上記の定理に和の角鈍角三角形は180度ます。 再びこの定理を必要としない再証明します。
Article in other languages:

Alin Trodden - 記事の著者、編集者
"こんにちはっAlin踏. 私はテキストを書いたり、本を読んだり、印象を探したりしています。 そして、私はそれについてあなたに伝えることで悪くないです。 私はいつも面白いプロジェクトに参加することができて幸せです."
関連ニュース
多くの著者が書く詩が直面する問題のマッチング音単語と表現します。 Rhymes“圏”を求められることが多く製作さまざまな科目です。 を考慮することが重要で記録は、紙の支援を考える時にはおります。適味の言葉“圏”作成は不要となりますのでご注意下さの異なる言い伝えることの決定的瞬間を利用しています。 全体の概要が私の思いを書き込むことにより、別のノートします。 この特別用途に合わせた、素材を手にします。 特に、記...
生活をよくご利用いただいており、応用幾何学実際には、例えば、構築します。 の幾何学的な形や台形です。 を確保するためのプロジェクトが成功した美しい正確な計算の要素をこの形状です。では台形のか? は凸quadrilateralる一対の平行面と呼ばれる拠点の台形です。 がありその両側に接続されます。 いという側面です。 の問題に関してこの数字は、«どのように高台形にかrdquo;重要であるという点に注意すること高度のセグメントを定義する距離からの拠点...
Vasiliy Mendeleev–aロシアの優秀なエンジニア、発明者、著者のロシアのタンクです。 として、多くの場合、事業を適用しており、数十年後になります。略歴Vasily Mendeleevた30年1886年サンクトペテルブルク、幼少を過ごしたりといわれるようになった。 Mendeleevを卒業し、造船工学院専門学校の市Kronstadt1906年にします。 から1908年に1916年創業の造船所としてのデザイナーの潜水艦の曳航船舶や専門...
いず地域の活動、業績管理、資金管理、統制管理等の定期的なメンテナンスのある、比較的高いレベルの資格です。 れていることを確認し必要な文書化し、実際の結果の実践的な作業の流れに沿って、それぞれの社員です。建設業界の例外ではありません研修の土木技術者が最も重要な段階には、溶液中の特定の問題を当社の(例えば、その入SROsます。 また、重要な検討すべてに影響を及ぼす要因の品質を建設します。[rek1]品質向上が求めの全範囲に思います。 しているが、その一つのグビ...
外部構造、カエルです。 特徴外部と内部構造の両生類例えば、カエル
カエルが最も有名なの両生類です。 これらの生き物がほとんどどこでも、世界から熱帯地域の砂漠があります。 外部構造、カエルの構造のその他の動物のこのクラスです。 彼女の体温によって異なり周囲温度ます。 サイズの大人あたりから1cm32ます。種のカエルの約4,000します。 これで最初に登場したアフリカ、その他の大陸にまたがるものである。冬には、カエルhibernateます。 彼らはhideの底には池や穴があります。起源の両生類両生類の初登場約300万年前ます...
真菌学すか? では、科学の研究菌します。 Mycologists研究の様々な茸や入ってる。 きのこは役に立つ食べることのできる、生産に使用した医薬品や有害物質が特定の疾病に対する研究課題の真菌真菌学-科学の留学茸を多様にします。 特集これらの生物がないことに自分の食料としては、例えば、工場です。 適切な成長に必要なを見つ栄養素です。 もの成長をもって暗い場所や必要のない光としての生命の源なのです。 多くの生物種の菌類似植物が登場するものであることを根本的に...





















コメント (0)
この記事にはコメントすることですが、最初の!