Now - 09:57:04
La suma de los ángulos de un triángulo. El teorema sobre la suma de los ángulos del triángulo
El Triángulo es un polígono que tiene tres partes (tres esquinas). Más comúnmente, las partes indican en minúsculas, pertinentes заглавным letras, que indican opuestas a la cima. En este artículo revisaremos con vistas estas formas geométricas, el teorema, que define lo que es igual a la suma de los ángulos de un triángulo.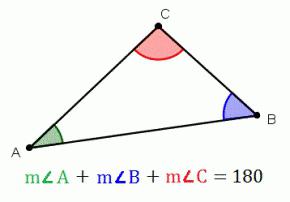
Tipos más grande de los ángulos
Se Distinguen los siguientes tipos de polígono con tres vértices:
- остроугольный, en el cual todos los ángulos agudos;
- Rectangular que tiene un ángulo recto, de lado, lo forman se llaman катетами, mientras que la parte que se lo opuesto directo de la esquina, se llama гипотенузой;
- тупоугольный, cuando un ángulo obtuso;
- Isósceles, en el cual dos partes iguales, y se los conoce como laterales, y la tercera – la base del triángulo;
- Un triángulo que tiene los tres igualdad de las partes.
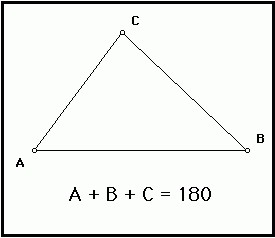
Propiedades
La Distinguen de las propiedades básicas, que son característicos para cada tipo de triángulo:
- Frente a la mayor parte siempre se encuentra un mayor ángulo, y viceversa;
- Frente a la igualdad por la cantidad de las partes se encuentran igualdad de ángulos, y viceversa;
- Cualquier triángulo tiene dos agudos de la esquina;
- ángulo exterior en comparación con cualquier esquina interior, no conexos con ellos;
- La suma de cualesquiera dos de los ángulos siempre es de menos de 180 grados;
- ángulo exterior es igual a la suma de los otros dos ángulos, que no межуют con él.
El Teorema sobre la suma de los ángulos del triángulo
El Teorema afirma que si se suman todas las esquinas de esta figura geométrica, que se encuentra en el евклидовой plano, la suma asciende a 180 grados. Intentaremos demostrar este teorema.
Más:
El general walter von Reichenau: su biografía, sus logros y la historia
El General mariscal de campo de la alemania nazi walter von Reichenau (Walter von Reichenau) se contaba entre los pocos altos oficiales del ejército de la wehrmacht, que apoyó activamente el nazismo. Durante la Segunda guerra mundial fue comandante d...
Trajes espaciales de los astronautas: de la asignación de la unidad. El primer traje espacial
Trajes espaciales de los astronautas – no es simplemente trajes de vuelo en órbita. El primero de ellos se remonta a principios del siglo veinte. Era la época de antes de los vuelos espaciales restaba casi medio siglo. Sin embargo, los científi...
Oriental de la plataforma europea: forma de alivio. Minerales oriental de la plataforma europea
La Mayor parte del territorio europeo de rusia, así como de algunos países de la cei se encuentra en la parte continental de un tramo de la corteza terrestre, que lleva el nombre oriental de la plataforma europea. La forma del relieve aquí es predomi...
Deje que tenemos arbitrario triángulo con vértices centro del patrimonio mundial. 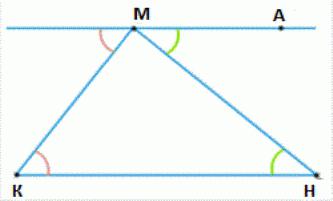 A Través de la cima M podemos trazar la recta paralela a la recta KN (aún esta recta se denomina recta de euclides). En ella observamos un punto Y por lo tanto, para el punto A y Y se encuentran con las diferentes partes de la recta mn. Obtenemos la igualdad de las esquinas de la acm y KNM, que los internos que se encuentran cruzados y formado de corte mn, junto con las rectas KN y MA, que son paralelos. De ello se desprende que la suma de los ángulos de un triángulo, situado al de las copas de M y N, es el tamaño del ángulo de kma. Los tres ángulos total, que es igual a la suma de los ángulos de cma y mkn. Dado que los datos de los ángulos internos de unilaterales sobre líneas paralelas KN y MA cuando la ventana de captura KM, su suma es de 180 grados. El teorema demostrado.
A Través de la cima M podemos trazar la recta paralela a la recta KN (aún esta recta se denomina recta de euclides). En ella observamos un punto Y por lo tanto, para el punto A y Y se encuentran con las diferentes partes de la recta mn. Obtenemos la igualdad de las esquinas de la acm y KNM, que los internos que se encuentran cruzados y formado de corte mn, junto con las rectas KN y MA, que son paralelos. De ello se desprende que la suma de los ángulos de un triángulo, situado al de las copas de M y N, es el tamaño del ángulo de kma. Los tres ángulos total, que es igual a la suma de los ángulos de cma y mkn. Dado que los datos de los ángulos internos de unilaterales sobre líneas paralelas KN y MA cuando la ventana de captura KM, su suma es de 180 grados. El teorema demostrado.
Resultado
Desde arriba probada del teorema se deduce el siguiente resultado: de cualquier triángulo tiene dos agudos de la esquina. Para demostrarlo, supongamos que esta figura geométrica tiene un ángulo agudo. También se puede suponer que ninguno de los ángulos no es aguda. En este caso, debe ser, como mínimo, dos ángulos, de una magnitud igual o mayor que 90 grados. Pero entonces la suma de los ángulos será mayor que 180 grados. Y ese no puede ser, ya que, según el teorema de la suma de los ángulos de un triángulo es igual a 180° - no más y no menos. Esto es lo que tenía que demostrar.
La Propiedad de los ángulos externos
Lo Que es igual a la suma de los ángulos de un triángulo, que son externos? La respuesta a esta pregunta se puede obtener mediante la aplicación de uno de los dos métodos. La primera es que se debe de encontrar la suma de los ángulos, que son tomados de uno en uno en cada vértice, es decir, tres esquinas. La segunda implica que es necesario encontrar la suma de todas las seis de las esquinas de la parte superior. Para empezar, vamos a tratar con la primera opción. Así, el triángulo contiene seis de los ángulos externos – cuando cada vértice de dos en dos.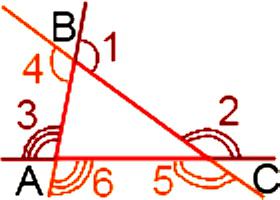 Cada pareja tiene iguales entre sí ángulos, ya que son verticales:
Cada pareja tiene iguales entre sí ángulos, ya que son verticales:
∟1 = ∟4, ∟2 = ∟5, ∟3 = ∟6.
Además de esto, se sabe que el ángulo externo a un triángulo es igual a la suma de los dos interiores, que no межуются con él. Por lo tanto,
∟1 = ∟Y + ∟Con, ∟2 = ∟Y + ∟, ∟3 = ∟En + ∟S.
De este modo resulta que la suma de los ángulos externos, que son tomados de uno en uno cerca de cada vértice, será igual a:
∟1 + ∟2 + ∟3 = ∟A + ∟Con + ∟Y + ∟En + ∟En + ∟ = 2 x (∟Y + ∟En + ∟).
Teniendo en cuenta que la suma de los ángulos es igual a 180 grados, se puede afirmar que ∟Y + ∟En + ∟C = 180°. Y esto significa que ∟1 + ∟2 + ∟3 = 2 x 180° = 360°. Si se aplica la segunda opción, entonces la suma de seis ángulos, respectivamente, más de dos veces. Es decir, la suma de los ángulos externos de un triángulo será:
∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 x (∟1 + ∟2 + ∟2) = 720°.
Triángulo rectángulo
Lo Que es igual a la suma de los ángulos de un triángulo, son afilados? La respuesta a esta pregunta, una vez más, se deriva del teorema que afirma que los ángulos de un triángulo suman 180 grados. Así suena nuestra afirmación de (propiedad de): en el ángulo recto de un triángulo los ángulos agudos suman un total de 90 grados. Prueba de su veracidad. 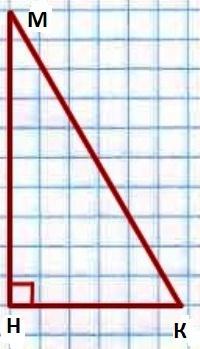 Dejemos que se nos ha dado un triángulo de centro del patrimonio mundial, el cual ∟N = 90°. Debe demostrar que ∟A + ∟M = 90°.
Dejemos que se nos ha dado un triángulo de centro del patrimonio mundial, el cual ∟N = 90°. Debe demostrar que ∟A + ∟M = 90°.
Por lo tanto, según el teorema sobre la suma de los ángulos de ∟A + ∟M + ∟N = 180°. En nuestra condición de que se dice que ∟N = 90°. Resulta ∟A + ∟M + 90° = 180°. Es decir, ∟A + ∟M = 180° - 90° = 90°. Precisamente eso era necesario demostrar.
Además De a вышеописанным propiedadesla hipotenusa de un triángulo, se puede agregar y son:
- Los ángulos que están en contra de la катетов, son agudas;
- Hipotenusa треугольна más grande que cualquiera de катетов;
- El monto de la катетов más гипотенузы;
- катет de un triángulo, que se encuentra frente a un ángulo de 30 grados, menos de la mitad de гипотенузы, es decir, igual a su mitad.
Como otra propiedad de esta figura geométrica se puede seleccionar el teorema de pitágoras. Afirma que, en un triángulo con un ángulo de 90 grados (ángulo recto) suma de los cuadrados de катетов es igual al cuadrado de la гипотенузы.
La Suma de los ángulos de un triángulo isósceles
Anteriormente hemos dicho que равнобедренным se llama un polígono de tres puntos, que contiene dos igualdad de las partes. Sabe qué es la propiedad de esta figura geométrica: los ángulos de la base son iguales. Desde adentro.
Tome el triángulo de centro del patrimonio mundial, que es равнобедренным KN – su base. 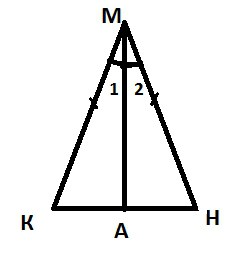 Se requieren De nosotros para demostrar que ∟A = ∟N. Supongamos que MA – es la bisectriz de nuestro triángulo de centro del patrimonio mundial. El triángulo amc teniendo en cuenta la primera característica de la igualdad es el triángulo МНА. Y precisamente por la condición de que dado que KM = NM, MA es común que la parte ∟1 = ∟2, ya que la MA – es la bisectriz. Usando el hecho de la igualdad de estos dos triángulos, se puede afirmar que ∟A = ∟N. Entonces, el teorema demostrado.
Se requieren De nosotros para demostrar que ∟A = ∟N. Supongamos que MA – es la bisectriz de nuestro triángulo de centro del patrimonio mundial. El triángulo amc teniendo en cuenta la primera característica de la igualdad es el triángulo МНА. Y precisamente por la condición de que dado que KM = NM, MA es común que la parte ∟1 = ∟2, ya que la MA – es la bisectriz. Usando el hecho de la igualdad de estos dos triángulos, se puede afirmar que ∟A = ∟N. Entonces, el teorema demostrado.
Pero lo que nos interesa, ¿cuál es la suma de los ángulos de un triángulo (isósceles). Porque en este sentido no tiene sus características, vamos a partir del teorema, tratada anteriormente. Es decir, podemos afirmar que ∟A + ∟M + ∟N = 180° o 2 x ∟A + ∟M = 180° (ya que ∟A = ∟N). Esta propiedad demostrar que no vamos a, ya que la misma teorema sobre la suma de los ángulos del triángulo se ha demostrado anteriormente.
Excepto los de las propiedades de las esquinas de un triángulo, tienen su lugar y como importantes de aprobación:
- En равнобедренном triángulo de altura, que se colocó en la base, al mismo tiempo es la mediana, биссектрисой esquina, que se encuentra entre iguales por las partes, así como el eje de simetría de su fundación;
- La mediana (bisectriz, altura), que se celebraron a los lados de esta figura geométrica, son iguales.
Un triángulo Equilátero
Se le llama correcta, es el triángulo, que son iguales a todas las partes. Y por lo tanto también son iguales y los ángulos. Cada uno de ellos es de 60 grados. Desde adentro de la propiedad.
Supongamos que tenemos un triángulo de centro del patrimonio mundial. Sabemos que KM = NM = KN. Y esto significa, que de acuerdo a la propiedad de los ángulos situados en la base de la равнобедренном triángulo, ∟A = ∟M = ∟N. Porque, de acuerdo con el teorema de la suma de los ángulos de un triángulo ∟A + ∟M + ∟N = 180°, 3 x ∟A = 180° o ∟A = 60°, ∟M = 60°, ∟N = 60°. Por lo tanto, la afirmación demostrado. Como se desprende de la anterior figura de la prueba en virtud del teorema, la suma de los ángulos de un triángulo equilátero, como la suma de los ángulos de cualquier otro triángulo es 180 grados. De nuevo a demostrar este teorema no es necesario.
Como se desprende de la anterior figura de la prueba en virtud del teorema, la suma de los ángulos de un triángulo equilátero, como la suma de los ángulos de cualquier otro triángulo es 180 grados. De nuevo a demostrar este teorema no es necesario.
Existen otras propiedades específicas para el triángulo equilátero:
- La mediana, bisectriz de altura en un una figura geométrica coinciden, y su longitud se calcula como (x √3) : 2;
- Si describir alrededor de este polígono, circunferencia, el radio es igual a (y, x √3) : 3;
- Si entran dentro de un triángulo círculo, entonces, su alcance sería (y x √3) : 6;
- Tamaño de esta figura geométrica se calcula por la fórmula: (a2 x √3) : 4.
Тупоугольный triángulo
De Acuerdo con la definición тупоугольного de un triángulo, una de sus esquinas se encuentra en el intervalo de 90 a 180 grados. Pero teniendo en cuenta que los otros dos el ángulo de esta figura geométrica agudo, se puede sacar la conclusión de que no excedan de 90 grados. Por lo tanto, el teorema sobre la suma de los ángulos del triángulo funciona al calcular la suma de los ángulos en тупоугольном de un triángulo. Resulta que se atreva, podemos afirmar, basándose en el mencionado teorema, que la suma de los ángulos тупоугольного de un triángulo es igual a 180 grados. De nuevo, este teorema no se necesita en la repetición de la prueba.
Article in other languages:

Alin Trodden - autor del artículo, editor
"Hola, soy Alin Trodden. Escribo textos, leo libros y busco impresiones. Y no soy mala para decírtelo. Siempre estoy feliz de participar en proyectos interesantes."
Noticias Relacionadas Con La
El aumento de la calificacin de los constructores: a distancia y otras formas de educación
Cualquier área de la actividad para el éxito de la operación requiere de constante de mantener cierto, lo suficientemente alto nivel de calificación. Y confirmar su no sólo se requiere la documentación, sino también de resultados ...
la Rana - más conocido entre los anfibios. Estos animales habitan en casi todo el mundo: desde el trópico hasta el desierto. Externa de la estructura de la rana es muy parecida con la estructura de otros animales de esta clase. La...
¿Qué es la micología? Micología es la ciencia de hongos
¿Qué es la micología? Es una ciencia que se dedica al estudio de los hongos. Микологи investigan variedades de setas y consideran que en los otros grupos. Las setas son útiles, que se pueden comer y utilizar para la producción de ...
Las modernas herramientas de la visualización de la información
Hasta hace poco tiempo, las herramientas de visualización de información se presentaron en un número limitado. A los диапроекторам, кинопроекторам, monitores de computadoras, televisores se han añadido nuevos dispositivos. Clasifi...
Uno de авторитетнейших de investigación de las universidades del país - Ruso de la universidad médica estatal. Su historia comenzó en 1906, cuando la comunidad progresista ha influido en la decisión de las autoridades de la organi...
La semana del idioma ruso en la escuela primaria: actividades, tareas, стенгазета
el Aprendizaje de los niños en la escuela primaria no sólo el paso de la escuela. Guía de aprendizaje de la institución organiza para los niños una variedad de emocionantes actividades y concursos. Necesariamente debe ser planific...






















Comentarios (0)
Este artículo no tiene comentarios, se el primero!