Now - 08:11:30
Сума кутів трикутника. Теорема про суму кутів трикутника
Трикутник представляє собою багатокутник, що має три сторони (три кута). Найчастіше сторони позначають малими буквами, відповідними заголовним буквах, якими позначають протилежні вершини. У даній статті ми ознайомимося з видами цих геометричних фігур, теорема, яка визначає, чому дорівнює сума кутів трикутника.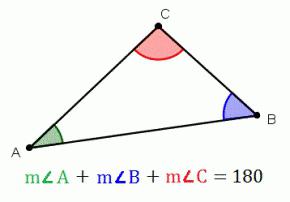
Види за величиною кутів
Розрізняють наступні види багатокутника з трьома вершинами:
- гострокутний, у якого всі кути гострі;
- прямокутний, має один прямий кут, при цьому сторони, що його утворюють, називають катетами, а сторона, яка розміщена протилежно прямого кута, називається гіпотенузою;
- тупокутний, коли один кут тупий;
- рівнобедрений, у якого дві сторони рівні, і вони називаються бічними, а третя – підставою трикутника;
- рівносторонній, який має всі три рівні сторони.
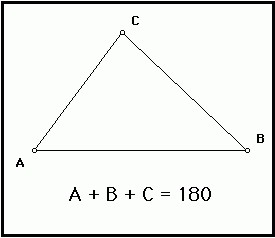
Властивості
Виділяють основні властивості, які характерні для кожного виду трикутника:
- навпроти більшої сторони завжди розташовується більший кут, і навпаки;
- навпроти рівних за величиною сторін знаходяться рівні кути, і навпаки;
- у будь-якого трикутника є два гострих кута;
- зовнішній кут більше порівняно з будь-яким внутрішнім кутом, не суміжних з ним;
- сума будь-яких двох кутів завжди менше 180 градусів;
- зовнішній кут дорівнює сумі двох інших кутів, які не межуют з ним.
Теорема про суму кутів трикутника
Теорема стверджує, що якщо скласти всі кути даної геометричної фігури, яка розташована на евклідової площини, то їх сума буде становити 180 градусів. Спробуємо довести цю теорему.
Більше:
Перший штучний супутник Землі є одним з найбільших досягнень науки ХХ століття. Тим не менш, як це ні парадоксально, цьому великому науковому і технічному досягненню значною мірою сприяла холодна війна між двома наддержавами: США і Радянським Союзом....
Що таке соціалізація, і як вона змінює людину
Спробуємо розібратися, що таке соціалізація, в чому її сутність і особливість. Адже для кожної особистості входження у суспільство і засвоєння його основних норм є фундаментом до подальшої безпроблемною і успішного життя і діяльності. Отже, що таке с...
Принц Чарльз – головний спадкоємець британського престолу
Згідно із законом королівства Великобританія, спадкоємець британського престолу - це старший закононароджена син чинного монарха або ж попереднього претендента на престол. Однак якщо у царюючого особи немає дитини чоловічої статі, то право спадкуванн...
Нехай у нас є довільний трикутник з вершинами КМН. 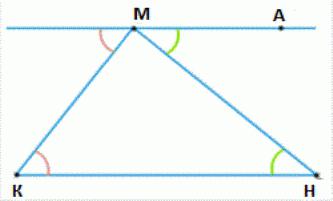 Через вершину М проведемо пряму паралельно прямій КН (ще цю пряму називають прямою Евкліда). На ній відзначимо точку А таким чином, щоб точки К і А були розташовані з різних боків прямої МН. Ми отримуємо рівні кути АМН і КНМ, які, як і внутрішні, лежать навхрест і утворюються січної МН спільно з прямими КН і МА, які є паралельними. З цього випливає, що сума кутів трикутника, розташованих при вершинах М і Н, що дорівнює розміру кута КМА. Всі три кута становлять суму, яка дорівнює сумі кутів КМА і МКН. Оскільки ці кути є внутрішніми односторонніми щодо паралельних прямих КН і МА при січної КМ, їх сума складає 180 градусів. Теорема доведена.
Через вершину М проведемо пряму паралельно прямій КН (ще цю пряму називають прямою Евкліда). На ній відзначимо точку А таким чином, щоб точки К і А були розташовані з різних боків прямої МН. Ми отримуємо рівні кути АМН і КНМ, які, як і внутрішні, лежать навхрест і утворюються січної МН спільно з прямими КН і МА, які є паралельними. З цього випливає, що сума кутів трикутника, розташованих при вершинах М і Н, що дорівнює розміру кута КМА. Всі три кута становлять суму, яка дорівнює сумі кутів КМА і МКН. Оскільки ці кути є внутрішніми односторонніми щодо паралельних прямих КН і МА при січної КМ, їх сума складає 180 градусів. Теорема доведена.
Слідство
З вище доведеної теореми випливає наступне наслідок: будь трикутник має два гострих кута. Щоб це довести, припустимо, що дана геометрична фігура має всього один гострий кут. Також можна припустити, що ні один із кутів не є гострим. В цьому випадку повинно бути як мінімум два кута, величина яких дорівнює або більше 90 градусів. Але тоді сума кутів буде більше, ніж 180 градусів. А такого бути не може, оскільки згідно з теоремою сума кутів трикутника дорівнює 180° - не більше і не менше. Ось це і потрібно було довести.
Властивість зовнішніх кутів
Чому дорівнює сума кутів трикутника, які є зовнішніми? Відповідь на це питання можна отримати, застосувавши один з двох способів. Перший полягає в тому, що необхідно знайти суму кутів, які взяті по одному при кожній вершині, тобто трьох кутів. Другий передбачає, що потрібно знайти суму всіх шести кутів при вершинах. Для початку розберемося з першим варіантом. Отже, трикутник містить шість зовнішніх кутів – при кожній вершині на два.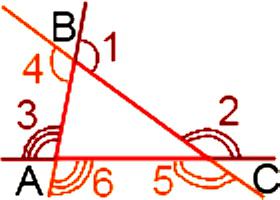 Кожна пара має рівні між собою кути, оскільки вони є вертикальними:
Кожна пара має рівні між собою кути, оскільки вони є вертикальними:
∟1 = ∟4, ∟2 = ∟5, ∟3 = ∟6.
Крім цього, відомо, що зовнішній кут у трикутника дорівнює сумі двох внутрішніх, які не межуються з ним. Отже,
∟1 = ∟А + ∟, ∟2 = ∟А + ∟, ∟3 = ∟В + ∟С.
З цього виходить, що сума зовнішніх кутів, які взяті по одному біля кожної вершини, буде дорівнює:
∟1 + ∟2 + ∟3 = ∟А + ∟З + ∟А + ∟В + ∟В + ∟З = 2 х (∟А + ∟В + ∟С).
З урахуванням того, що сума кутів дорівнює 180 градусам, можна стверджувати, що ∟А + ∟В + ∟С = 180°. А це означає, що ∟1 + ∟2 + ∟3 = 2 х 180° = 360°. Якщо ж застосовується другий варіант, то сума шести кутів буде, відповідно, більшою в два рази. Тобто сума зовнішніх кутів трикутника буде становити:
∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 х (∟1 + ∟2 + ∟2) = 720°.
Прямокутний трикутник
Чому дорівнює сума кутів прямокутного трикутника, які є гострими? Відповідь на це питання, знову ж таки, випливає з теореми, яка стверджує, що в трикутнику кути в сумі становлять 180 градусів. А звучить наше твердження (властивість) так: у прямокутному трикутнику гострі кути в сумі дають 90 градусів. Доведемо його правдивість. 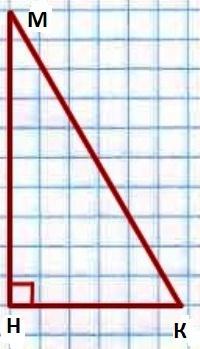 Нехай нам дано трикутник КМН, у якого ∟Н = 90°. Необхідно довести, що ∟До + ∟М = 90°.
Нехай нам дано трикутник КМН, у якого ∟Н = 90°. Необхідно довести, що ∟До + ∟М = 90°.
Отже, згідно з теоремою про суму кутів ∟До + ∟М + ∟Н = 180°. У нашому умові сказано, що ∟Н = 90°. Ось і виходить, ∟До + ∟М + 90° = 180°. Тобто ∟До + ∟М = 180° - 90° = 90°. Саме це нам і треба було довести.
На додаток до описаних вище властивостейпрямокутного трикутника, можна додати й такі:
- кути, що лежать проти катетів, є гострими;
- гіпотенуза треугольна більше будь-якого з катетів;
- сума катетів більше гіпотенузи;
- катет трикутника, який лежить навпроти кута 30 градусів, в два рази менше гіпотенузи, тобто дорівнює її половині.
Як ще одна властивість даної геометричної фігури можна виділити теорему Піфагора. Вона стверджує, що в трикутнику з кутом 90 градусів (прямокутній) сума квадратів катетів дорівнює квадрату гіпотенузи.
Сума кутів рівнобедреного трикутника
Раніше ми говорили, що називають рівнобедреним багатокутник з трьома вершинами, що містить дві рівні сторони. Відомо таке властивість даної геометричної фігури: кути при основі рівні. Доведемо це.
Візьмемо трикутник КМН, який є рівнобедреним, КН – його основу. 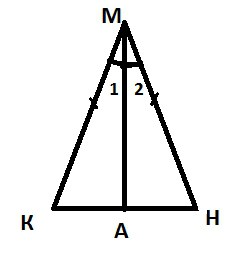 Від нас потрібно довести, що ∟До = ∟Н. Отже, припустимо, що МА – це бісектриса нашого трикутника КМН. Трикутник МКА з урахуванням першої ознаки рівності дорівнює трикутнику МНА. А саме за умовою дано, що КМ = НМ, МА є спільною стороною, ∟1 = ∟2, оскільки МА – це бісектриса. Використовуючи факт рівності цих двох трикутників, можна стверджувати, що ∟До = ∟Н. Отже, теорема доведена.
Від нас потрібно довести, що ∟До = ∟Н. Отже, припустимо, що МА – це бісектриса нашого трикутника КМН. Трикутник МКА з урахуванням першої ознаки рівності дорівнює трикутнику МНА. А саме за умовою дано, що КМ = НМ, МА є спільною стороною, ∟1 = ∟2, оскільки МА – це бісектриса. Використовуючи факт рівності цих двох трикутників, можна стверджувати, що ∟До = ∟Н. Отже, теорема доведена.
Але нас цікавить, яка сума кутів трикутника (рівнобедреного). Оскільки в цьому відношенні у нього немає своїх особливостей, будемо відштовхуватися від теореми, розглянутої раніше. Тобто ми можемо стверджувати, що ∟До + ∟М + ∟Н = 180°, або 2 х ∟До + ∟М = 180° (оскільки ∟До = ∟Н). Дана властивість доводити не будемо, оскільки сама теорема про суму кутів трикутника була доведена раніше.
Крім розглянутих властивостей про кутах трикутника, мають місце і такі важливі твердження:
- равнобедренном трикутнику висота, яка була опущена на основу, є одночасно медіаною, бісектрисою кута, який знаходиться між рівними сторонами, а також віссю симетрії його заснування;
- медіани (бісектриси, висоти), які проведені до бічних сторін такої геометричної фігури, рівні.
Рівносторонній трикутник
Його ще називають правильним, це той трикутник, у якого дорівнюють всі сторони. А тому рівні також і кути. Кожен з них становить 60 градусів. Доведемо цю властивість.
Припустимо, що у нас є трикутник КМН. Нам відомо, що КМ = НМ = КН. А це означає, що згідно властивості кутів, розташованих при основі в равнобедренном трикутнику, ∟До = ∟М = ∟Н. Оскільки згідно з теоремою сума кутів трикутника ∟До + ∟М + ∟Н = 180°, 3 х ∟До = 180° або ∟До = 60°, ∟М = 60°, ∟Н = 60°. Таким чином, твердження доведено. Як видно з вище наведеного докази на підставі теореми, сума кутів рівностороннього трикутника, як і сума кутів будь-якого іншого трикутника, складає 180 градусів. Знову доводити цю теорему немає необхідності.
Як видно з вище наведеного докази на підставі теореми, сума кутів рівностороннього трикутника, як і сума кутів будь-якого іншого трикутника, складає 180 градусів. Знову доводити цю теорему немає необхідності.
Існують ще такі властивості, характерні для рівностороннього трикутника:
- медіана, бісектриса, висота до такої геометричної фігури збігаються, а їх довжина обчислюється як (а х √3) : 2;
- якщо описати навколо даного багатокутника окружність, то її радіус дорівнює (а х √3) : 3;
- якщо вписати в рівносторонній трикутник коло, то її радіус буде становити (а х √3) : 6;
- площа цієї геометричної фігури обчислюється за формулою: (а2 х √3) : 4.
Тупокутний трикутник
Згідно з визначенням тупоугольного трикутника, один з кутів знаходиться в проміжку від 90 до 180 градусів. Але враховуючи те, що два інших кута даної геометричної фігури гострі, можна зробити висновок, що вони не перевищують 90 градусів. Отже, теорема про суму кутів трикутника працює при розрахунку суми кутів у тупоугольном трикутнику. Виходить, ми сміливо можемо стверджувати, спираючись на вищезгадану теорему, що сума кутів тупоугольного трикутника дорівнює 180 градусам. Знову-таки, ця теорема не потребує повторного доведення.
Article in other languages:

Alin Trodden - автор статті, редактор
"Привіт, Я Алін Тродден. Я пишу тексти, читаю книги і шукаю враження. І я непогано вмію розповідати вам про це. Я завжди радий брати участь у цікавих проектах."
Новини
Підвищення кваліфікації будівельників: дистанційно та інші форми навчання
Будь-яка область діяльності для успішної роботи вимагає постійного підтримання певного, досить високого кваліфікаційного рівня. І підтверджувати його потрібно не тільки документально, але і з реальними результатами практичної робо...
Зовнішня будова жаби. Особливості зовнішньої та внутрішньої будови земноводних на прикладі жаби
Жаби - найвідоміші серед земноводних. Ці тварини мешкають практично в усьому світі: від тропіків до пустелі. Зовнішня будова жаби дуже схоже з будовою інших тварин цього класу. Температура її тіла змінюється залежно від температур...
Що таке мікологія? Мікологія - наука про гриби
Що таке мікологія? Це наука, яка займається вивченням грибів. Мікологи досліджують різновиди грибів і відносять їх у ті чи інші групи. Гриби бувають корисними, які можна вживати в їжу та використовувати для виробництва лікарських ...
Як підготуватися до іспиту за 1 день до його здачі: способи та рекомендації
Практично кожен чоловік був студентом. І відповідно, багато хто з нас знають, що собою являє сесія. Вона неминуча, як і здача іспитів. Але життя студента сповнена цікавих подій, і в багатьох навчання стоїть далеко не на першому мі...
Сучасні засоби відображення інформації
До недавнього часу засоби відображення інформації були представлені в обмеженій кількості. До традиційних диапроекторам, кинопроекторам, моніторів комп'ютерів, телевізорів додалися нові пристрої. Класифікація засобів відображення ...
Один з авторитетних дослідницьких вузів країни - Російський державний медичний університет. Історія його почалася в 1906 році, коли прогресивна громадськість вплинула на рішення влади для організації Московських жіночих курсів. Че...






















Примітка (0)
Ця стаття не має коментарів, будьте першим!