की राशि के दृष्टिकोण के त्रिकोण है. योग के एक त्रिकोण के कोण

एक त्रिकोण है एक बहुभुज के साथ तीन पक्षों (तीन कोण). सबसे अक्सर पार्टियों का संकेत होगा छोटे अक्षरों में इसी राजधानी पत्र के लिए जो नामित विपरीत कोने है. इस अनुच्छेद में हम पर एक नज़र रखना, इन ज्यामितीय आकृतियों प्रमेय है, जो निर्धारित करता है क्या है की राशि के बराबर एक त्रिकोण के कोण है । <आइएमजी alt="योग के एक त्रिकोण के कोण" ऊंचाई="202" src="/images/2018-Mar/17/4974eef538f20e8ddc615d373241469a/1.jpg" चौड़ाई="290" />

दर्शनों की संख्या के मूल्य पर कोण

निम्नलिखित प्रकार के बहुभुज के साथ केवल तीन कोने:

<उल>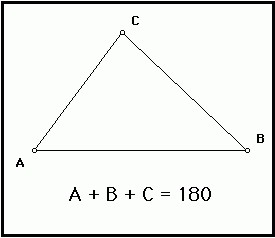

तेज है, जो सभी कोणों तीव्र;

आयताकार, एक सही कोण के साथ, हाथ, अपनी फार्म कहा जाता है, पैर, और पक्ष रखा गया है, जो विपरीत सही कोण कर्ण कहा जाता है;

कुंठित, जब एक obtuse कोण;

समद्विबाहु है, जो दो पक्षों के बराबर हैं, और वे कर रहे हैं कहा जाता है पार्श्व, और तीसरे और ndash; त्रिकोण के आधार के लिए;

एक समभुज सभी पक्षों के बराबर है ।

गुण

आवंटित बुनियादी गुणों की विशेषता है कि प्रत्येक प्रकार के त्रिकोण:

<उल>

के सामने बड़ा पक्ष है हमेशा बड़ा कोण, और इसके विपरीत;

के के विपरीत के बराबर पक्षों के बराबर हैं कोण और इसके विपरीत;

हर त्रिकोण के दो तीव्र कोण;

बाह्य कोण की तुलना में अधिक है, किसी भी इंटीरियर कोण करने के लिए आसन्न नहीं है;

योग के किसी भी दो कोणों है, हमेशा कम से कम 180 डिग्री;

बाहरी कोण के बराबर की राशि को अन्य दो कोणों है कि नहीं कर रहे हैं maiwut उसके साथ.

का योग एक त्रिकोण के कोण

प्रमेय कहा गया है कि अगर आप जोड़ सभी कोणों ज्यामितीय आकृतियों में से एक में स्थित हैं, जो यूक्लिडियन विमान, तो उनके योग होगा 180 डिग्री से. चलो यह साबित करने की कोशिश इस प्रमेय.

चलो हम एक मनमाना त्रिकोण के कोने KMN. 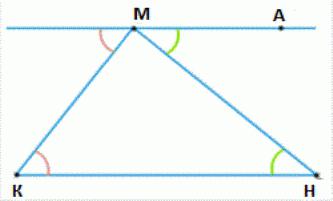का उपयोग कर शीर्ष मीटर समानांतर एक रेखा खींचना । लाइन के लिए KN (यह प्रत्यक्ष कॉल, प्रत्यक्ष यूक्लिड). यह मार्क एक बिंदु ऐसा है कि बात करने के लिए और स्थित थे के विभिन्न पक्षों पर सीधे MN. हम बराबर कोण AMN और KNM, जो, के रूप में आंतरिक, कर रहे हैं, क्रॉस सेक्शन है और का गठन कर रहे हैं MN के साथ एक साथ सीधा KN और मा है, जो समानांतर हैं. यह इस से इस प्रकार है कि योग की एक त्रिकोण के कोण पर स्थित कोने में M और N के बराबर होती है के आकार के कोण CMA है । सभी तीन कोणों का प्रतिनिधित्व करते हैं की राशि के बराबर है जो की राशि के दृष्टिकोण OMA और MCS. के बाद से इन कोणों के सापेक्ष आंतरिक एकतरफा समानांतर लाइनों KN और मा खंड पर किमी है, उनके योग 180 डिग्री से. प्रमेय साबित कर दिया है.

में परिणाम

से ऊपर प्रमेय का तात्पर्य निम्न परिणाम: किसी भी त्रिकोण के दो तीव्र कोण है । यह साबित करने के लिए, मान लीजिए कि इस ज्यामितीय आंकड़ा है, केवल एक तीव्र कोण है । आप कर सकते हैं यह भी मानते हैं कि कोई नहीं के कोण नहीं है गंभीर है । इस मामले में, आप होना चाहिए कम से कम दो कोणों का मूल्य है, जो करने के लिए बराबर या अधिक से अधिक 90 डिग्री है. लेकिन फिर कोणों का योग है अधिक से अधिक 180 डिग्री से. लेकिन यह नहीं हो सकता, क्योंकि के अनुसार प्रमेय कोणों का योग एक त्रिकोण के बराबर है करने के लिए 180 डिग्री; - कोई और भी कम नहीं है । की जरूरत है कि यह साबित करने के लिए.

संपत्ति के बाहरी कोनों पर

क्या है के कोणों का योग एक त्रिकोण है कि बाहरी हैं? इस सवाल का जवाब प्राप्त किया जा सकता का उपयोग दो तरीकों में से एक है । पहला यह है कि आप की जरूरत है खोजने के लिए की राशि के दृष्टिकोण लिया जाता है, जो एक शीर्ष स्तर पर प्रत्येक, यानी तीन कोण है । दूसरा अर्थ है कि आप की जरूरत है खोजने के लिए की राशि के सभी छह कोण पर कोने है. पहली चलो सौदे के साथ पहला विकल्प है । तो, एक त्रिकोण छह बाहरी कोण – और प्रत्येक शीर्ष दो है । <आइएमजी alt="योग के बाहरी कोण के साथ एक त्रिकोण" height="200" src="/images/2018-Mar/17/4974eef538f20e8ddc615d373241469a/4.jpg" width="280" /> प्रत्येक जोड़ी के बराबर कोण है, क्योंकि वे खड़ी कर रहे हैं:

∟1 = ∟4, ∟2 = ∟5, ∟3 = ∟6.

इसके अलावा, यह ज्ञात है कि बाहरी कोण के साथ एक त्रिकोण के बराबर की राशि के भीतर नहीं हैं, जो masouda उसके साथ है । इसलिए,

∟1 = ∟एक + ∟C, ∟2 = ∟एक + ∟में, ∟3 = ∟एक + ∟पी.

यह पता चला है कि योग के बाहरी कोण से लिया जाता है, जो एक शीर्ष स्तर पर प्रत्येक, बराबर हो जाएगा करने के लिए:

∟1 + ∟2 + ∟3 = ∟एक + ∟C + ∟एक + ∟एक + ∟एक + ∟C = 2 x (∟एक + ∟एक + ∟C).

इस तथ्य को देखते हुए कि कोणों का योग 180 डिग्री के बराबर होती है, यह तर्क दिया जा सकता है कि ∟एक + ∟एक + ∟C = 180 डिग्री है । इसका मतलब यह है कि ∟1 + ∟2 + ∟3 = 2 x 180 डिग्री = 360&डिग्री;. अगर दूसरा विकल्प लागू होता है, योग के छह कोण, क्रमशः, अधिक से अधिक दो बार. कि है, योग के बाहरी कोण के साथ एक त्रिकोण हो जाएगा:

∟1 + ∟2 + ∟3 + ∟4 + ∟5 + ∟6 = 2 x (∟1 + ∟2 + ∟2) = 720&डिग्री;.

सही त्रिकोण

क्या है की राशि के बराबर का कोण एक सही त्रिकोण तीव्र हैं? इस सवाल का जवाब है, फिर से, इस प्रकार से प्रमेय है, जो राज्यों है कि एक त्रिकोण में कोण का योग 180 डिग्री के लिए. और हमारे अनुमोदन (संपत्ति): एक सही त्रिकोण में तीव्र कोण 90 डिग्री के बराबर होती है. साबित अपनी सच्चाई है । 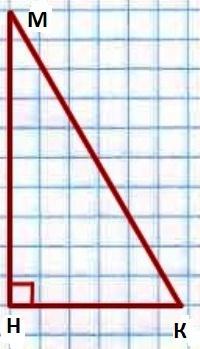हमें एक को देखते त्रिकोण KMN, जिसका ∟H = 90 डिग्री है. आप को साबित करना होगा कि ∟करने के लिए + ∟M = 90 डिग्री है ।

तो, के अनुसार प्रमेय के कोणों का योग ∟करने के लिए + ∟एम ∟H = 180 डिग्री है । हमारे हालत में कहते हैं ∟H = 90 डिग्री है. तो ∟करने के लिए + ∟M + 90 डिग्री; एक = 180 डिग्री है । कि है, ∟करने के लिए + ∟M = 180 डिग्री; से 90 डिग्री; = 90 डिग्री है. है कि क्या हम साबित करना चाहिए.

इसके अलावा करने के लिए ऊपर के गुणों कोएक सही त्रिकोण के साथ, आप कर सकते हैं निम्न जोड़ें:

<उल>

के के कोण जो झूठ के खिलाफ पैर, तीव्र कर रहे हैं;

कर्ण के त्रिकोण है अधिक से अधिक की तुलना में किसी भी अन्य दो पक्षों;

योग के पैर और अधिक के कर्ण;

पैर, त्रिकोण के विपरीत निहित है जो 30 डिग्री के कोण, दो बार से कम नहीं कर्ण है कि आधे के बराबर है.

के रूप में एक और संपत्ति के इस ज्यामितीय आकृति यह संभव है कि आवंटित करने के लिए पाइथागोरस प्रमेय. वह तर्क है कि एक त्रिकोण के साथ एक 90 डिग्री के कोण (सही कोण) के वर्गों का योग के पैर के बराबर होती है कर्ण के वर्ग के.

कोणों का योग एक समद्विबाहु त्रिकोण के

इससे पहले हम ने कहा है कि कहा जाता है समद्विबाहु के साथ एक बहुभुज केवल तीन कोने गया है कि दो पक्षों के बराबर हैं. यह ज्ञात है कि एक संपत्ति के इस ज्यामितीय आकृति: कोणों इसके आधार पर कर रहे हैं के बराबर है । यह साबित.

पर विचार एक त्रिकोण KMN, जो समद्विबाहु है, केएन – इसके आधार पर. 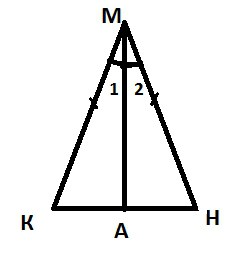हम कर रहे हैं साबित करने के लिए आवश्यक है कि ∟C = ∟N. तो, चलो का कहना है कि मा – हमारे द्विभाजक एक त्रिकोण के KMN. त्रिकोण μa के साथ का पहला संकेत में समानता है करने के लिए बराबर त्रिकोण MNA. अर्थात्, कि शर्त किमी = एनएम, मा एक सामान्य पार्टी, ∟1 = ∟2 के बाद से, मा – द्विभाजक है. का उपयोग कर समानता के दो त्रिकोण, यह तर्क दिया जा सकता है कि ∟C = ∟N. तो प्रमेय साबित कर दिया है.

मुझे आश्चर्य है कि, क्या है की राशि के कोण के साथ एक त्रिकोण (समद्विबाहु). क्योंकि इस संबंध में वह नहीं है, उसकी विशेषताओं, हम शुरू से प्रमेय पहले चर्चा की है । यही है, हम कह सकते हैं कि ∟करने के लिए + ∟एम ∟H = 180 डिग्री, या 2 x ∟करने के लिए + ∟M = 180 डिग्री (क्योंकि ∟C = ∟एन). इस संपत्ति साबित नहीं होगा, क्योंकि योग के एक त्रिकोण के कोण साबित कर दिया था पहले.

इसके अलावा करने के लिए के गुण एक त्रिकोण के कोण, वहाँ रहे हैं इस तरह के महत्वपूर्ण बयान:

<उल><ली>में एक समभुज त्रिकोण की ऊंचाई है, जो उतारा गया था, जमीन के लिए भी है, मंझला, द्विभाजक के कोण के बीच है, जो के बराबर पक्षों और समरूपता की धुरी की अपनी नींव;

मंझला (bisectors, ऊंचाई) है, जो आयोजित कर रहे हैं के पक्षों के लिए इस ज्यामितीय आंकड़ा के बराबर हैं ।

समभुज त्रिकोण

यह कहा जाता है उचित है, यह है कि त्रिकोण, जिनके सभी पक्षों के बराबर हैं । और इसलिए बराबर भी कोण से. उनमें से प्रत्येक के लिए 60 डिग्री है । हमें यह साबित संपत्ति है ।

मान लीजिए हम एक त्रिकोण KMN. हम जानते हैं कि किमी = एनएम = KN. इसका मतलब यह है कि के अनुसार संपत्ति कोनों के आधार पर स्थित समद्विबाहु त्रिकोण, ∟C = ∟एम ∟राष्ट्र के अनुसार के बाद से इस प्रमेय का योग एक त्रिकोण के कोण ∟करने के लिए + ∟एम ∟H = 180 डिग्री, 3 x ∟करने के लिए एक = 180 डिग्री; या ∟C = 60 डिग्री, ∟M = 60 डिग्री, ∟N = 60 डिग्री. इस प्रकार, इस दावे को साबित कर दिया है.<आइएमजी alt="कोणों का योग एक त्रिकोण के बराबर है" ऊंचाई="201" src="/images/2018-Mar/17/4974eef538f20e8ddc615d373241469a/7.jpg" चौड़ाई="495" />के रूप में आप ऊपर से देख सकते हैं सबूत के आधार पर प्रमेय, के कोणों का योग एक समभुज त्रिकोण के कोणों का योग के किसी भी अन्य त्रिकोण है, 180 डिग्री । फिर इस प्रमेय को साबित करने के लिए आवश्यक नहीं है.

वहाँ अभी भी कर रहे हैं इस तरह के गुणों की विशेषता एक समभुज त्रिकोण:

<उल>

मंझला, द्विभाजक, ऊंचाई में इस तरह के एक ज्यामितीय आंकड़ा के समान हैं और उनकी लंबाई के रूप में मूल्यांकन किया (x √3) : 2;

का वर्णन बहुभुज सर्कल के चारों ओर, इसकी त्रिज्या के बराबर हो जाएगा (x √3) : 3;

यदि आप लिखना एक समभुज त्रिकोण का एक चक्र में तो इसकी त्रिज्या हो जाएगा (x √3) : 6;

के के क्षेत्र में इस ज्यामितीय आकृति है, सूत्र द्वारा गणना की है: (A2 x √3) : 4 है ।

कुंठित त्रिकोण

की परिभाषा के अनुसार कुंठित त्रिकोण अपने कोनों में से एक रेंज में है करने के लिए 90 से 180 डिग्री से. लेकिन तथ्य यह है कि अन्य दो कोण दिए गए हैं ज्यामितीय आकृतियों तेज, हम निष्कर्ष निकाल सकते हैं कि वे अधिक नहीं 90 डिग्री से. इसलिए, योग के कोणों एक त्रिकोण का काम जब गणना की राशि के दृष्टिकोण में कुंठित त्रिकोण है. तो, हम सुरक्षित रूप से कह सकता, ऊपर के आधार पर प्रमेय है कि योग के कोण कुंठित-angled त्रिकोण 180 डिग्री के बराबर है. फिर से, इस प्रमेय की आवश्यकता नहीं है फिर से सबूत है.