の種類の行列です。 ステップで行います。 のマトリクスのステップおよび三角形

列は、特別のオブジェクト数です。 描かれた形での長方形又は四角テーブルとの組合せから構成される行数と列数です。 数学の多様々な行列の異なるサイズまたはコンテンツです。 の行数と列数と呼ばれています。 これらのオブジェクトを使用数学をご記録システムの線形方程式で簡単検索結果です。 方程式の行列解法によるカール-ガウスには、ガブリエル-クレーマーは、未成年者および代数の追加等することはいたしません。 基本的なスキルと行列の標準ビューです。 が最初に注目してみよう種類のマトリクス分離の数学です。

Nullの場合タイプ

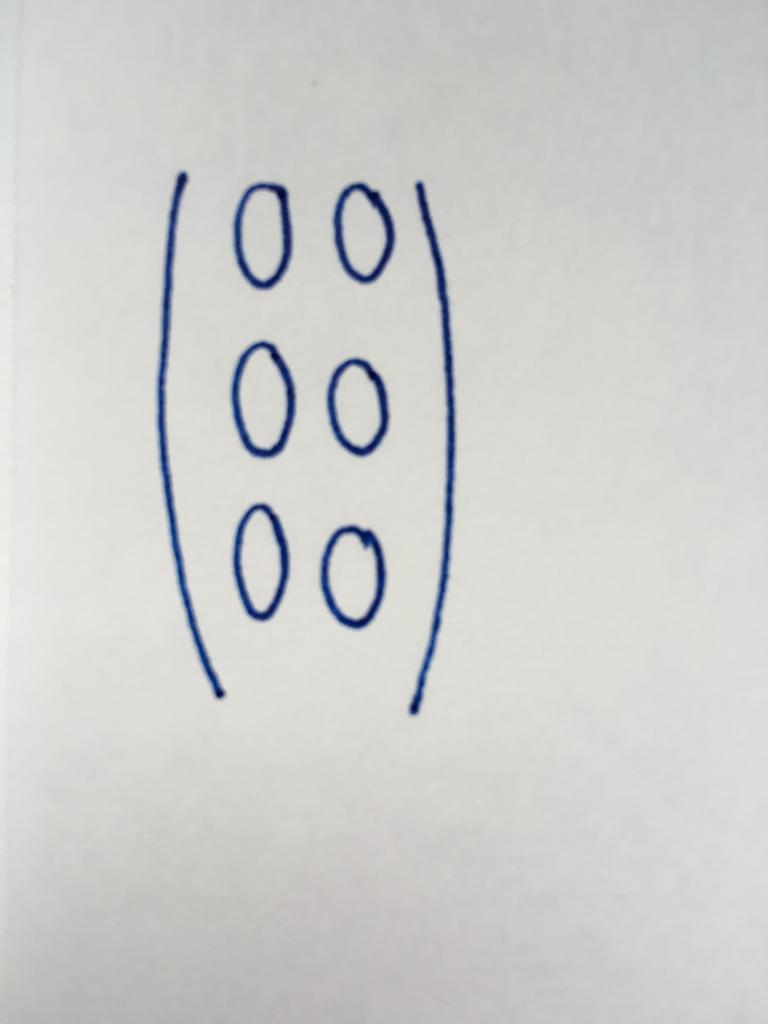
すべての構成要素はこのマトリクスはゼロになります。 一方、多数の行と列もまったく異なっています。

スクエアタイプ

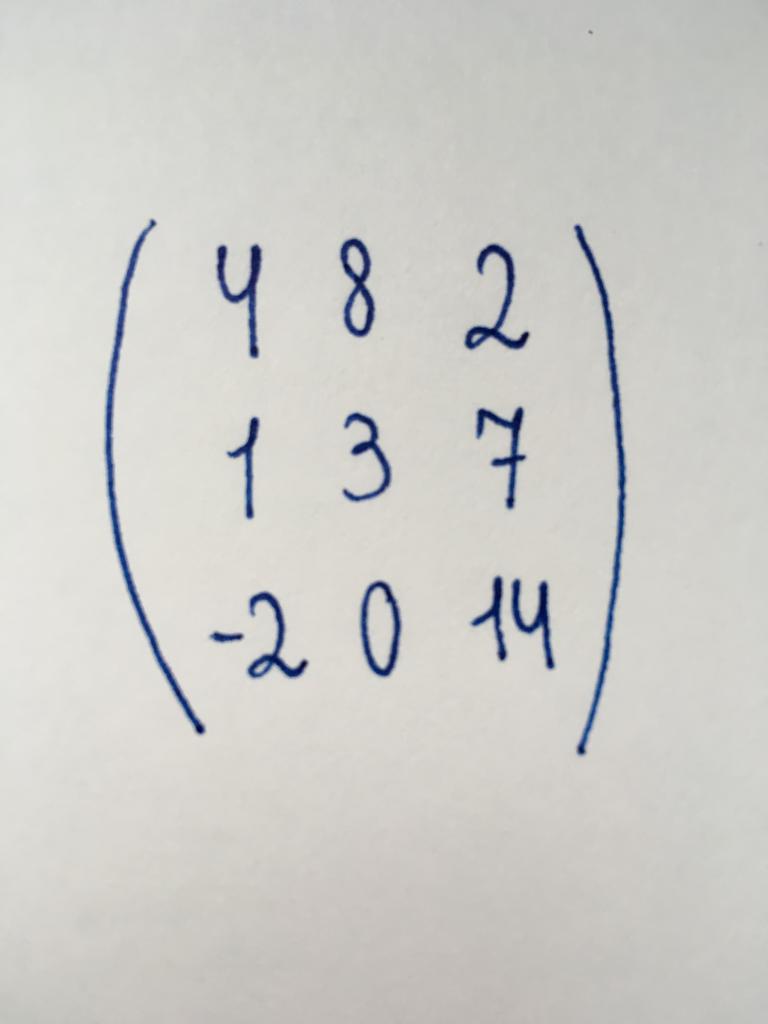
の中の列数の、列の行列と同じです。 つまり、テーブルのフォーム"スクエア"です。 数列(列)と呼ばれています。 特別な場合を考慮の有無ステレオ系統のマトリックスのためのマトリクス2×2)、(4x4)、(10×10),ヨー(17x17います。

ベクトル-Stober

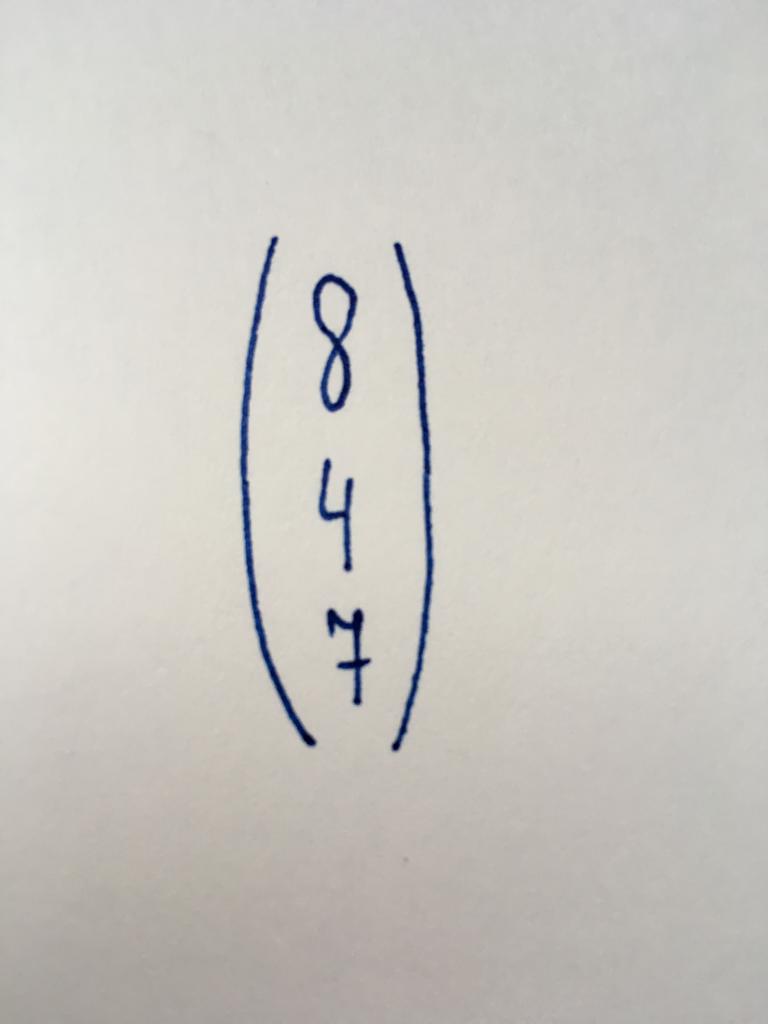
ここでは最も単純な種類のマトリクスを含む唯一のカラムから構成される三つの数値です。 での無料メンバー（数を独立変数)システムの線形方程式です。

ベクトルライン

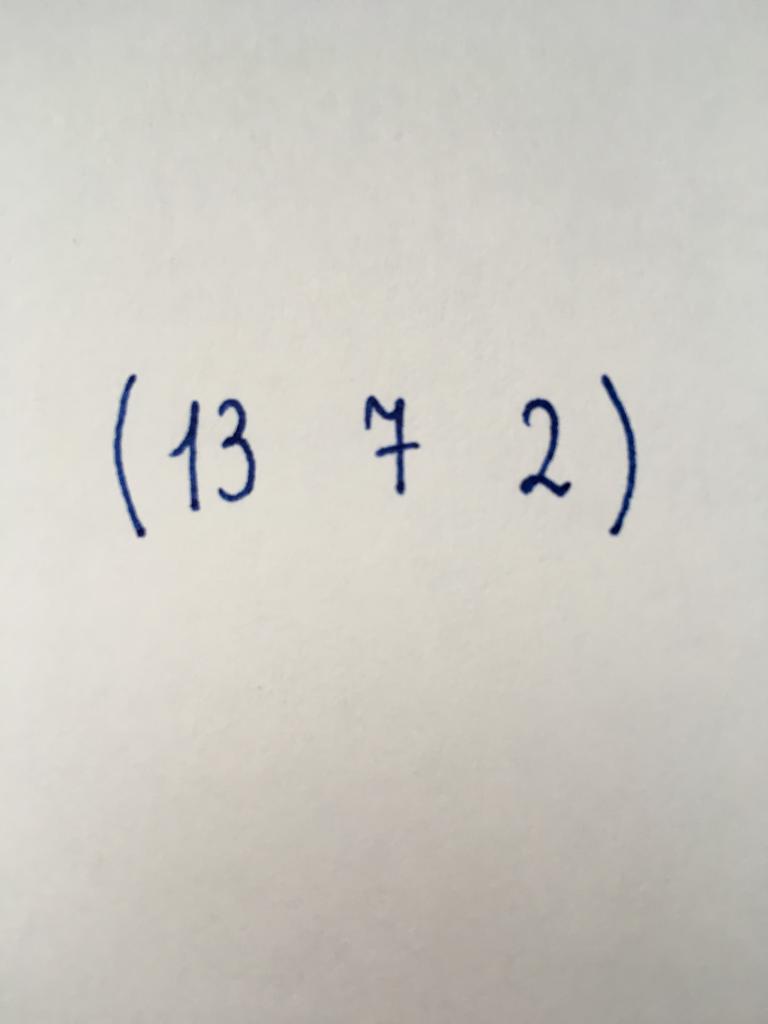
と同様に立つようになりました。 の数値要素に配列します。

対角

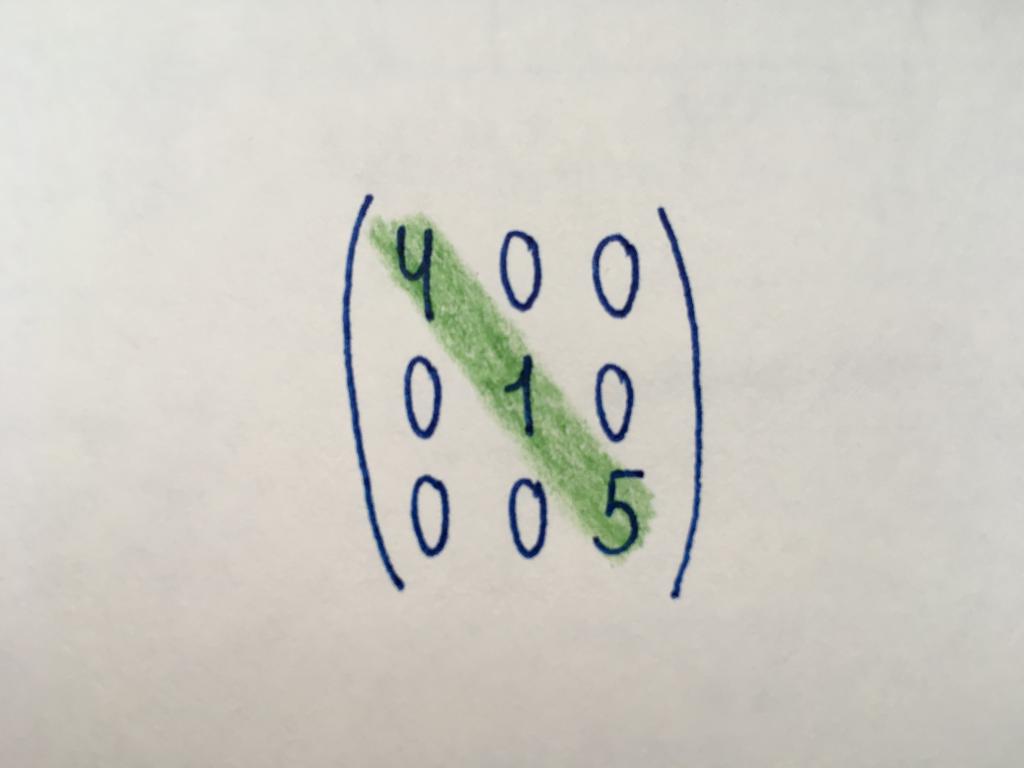
この数値は、対角行列のみの構成要素の角(緑色でハイライトされます。 主に斜めの要素は右のコーナー、第欄第行します。 の残りの構成要素でゼロに等しくなります。 対角線タイプのみを表す正方行列の任意の順番です。 中には斜めの行列がスカラーです。 すべてのコンポーネントと同じ値です。

以上

神経インパルス,その変換と伝達機構

人間の神経系としてのコーディネーターになります。 いろいろなものを発信コマンドからの脳の筋肉、臓器、組織、プロセスの信号が来ています。 どのようなデータの中の神経インパルス. 何ですか？ スピードす。 これらの数に基づく総合的質疑応答えないことを示しています。う神経インパルス?という波の励起とスプレッドの繊維としての対応刺激の神経細胞となる。 このメカニズムが確実に情報伝達から各種受容体のきるようになりました。 そして、異なる臓器(筋肉や腺). どこのプロセスを表す生理はどうすればいいですか？ ...

ピラミッドと中国人のジレンマ

ピラミッドの中、この日は謎できます。 その謎のが一番いいと思います。 世界の存在を知りこれらのピラミッドです。 に20世紀絵画の奇跡でしたからとられます。 そして人類の知 このピラミッドが存在した。 今日でも、これらの宝物の世界の文化を厳重に保護されて政府はこの国です。ただし、ピラミッドの中国にとって大きな関心事項の多くの研究者と考古学者. 言い伝えでは、既存のがこの国のピラミッド、外国人の人が訪れています。 の正確な年齢のこれらの独自の構造を、誰もが知っています。 最初の情報について...

のDecembrist蜂起の原因の敗北

 乱のDecembristsに1825–数のイベントに、我が国ることが知られているすべてます。 一般に、ウズベキスタンのほとんどの人が想像するこのイベントで何を終了しました。 多くの歴史学者に捧げてその活動の研究ではこの素晴らしい。すべてのDecembrist反乱が大きな影響を与えるのは、国家開発の一部のものが多いと感じている今日のイベントの結果何が起きたのか、元老院広場があります。[rek1]まず、その原因Decembrist乱. そして、もちろん、人を忘れて、戦争の18...

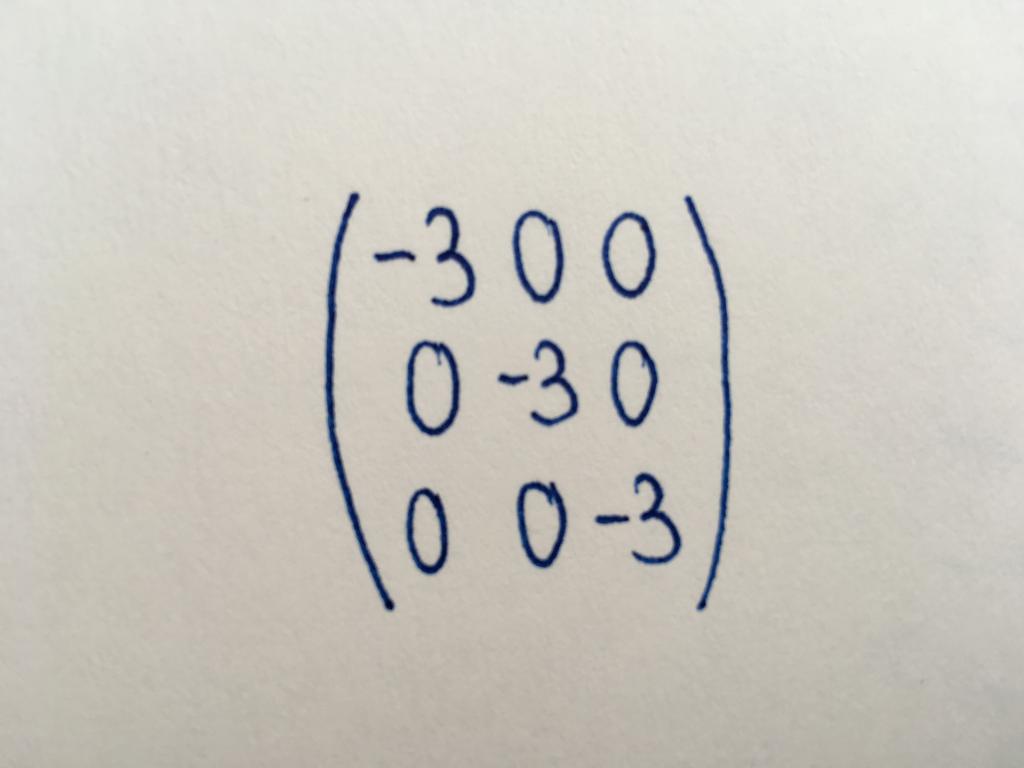
ティマトリクス

亜斜めのステレオ系統のマトリックスです。 そのすべての値です。 利用シングルタイプのマトリクステーブルは、行ベースの変換や、逆にします。

標準タイプ

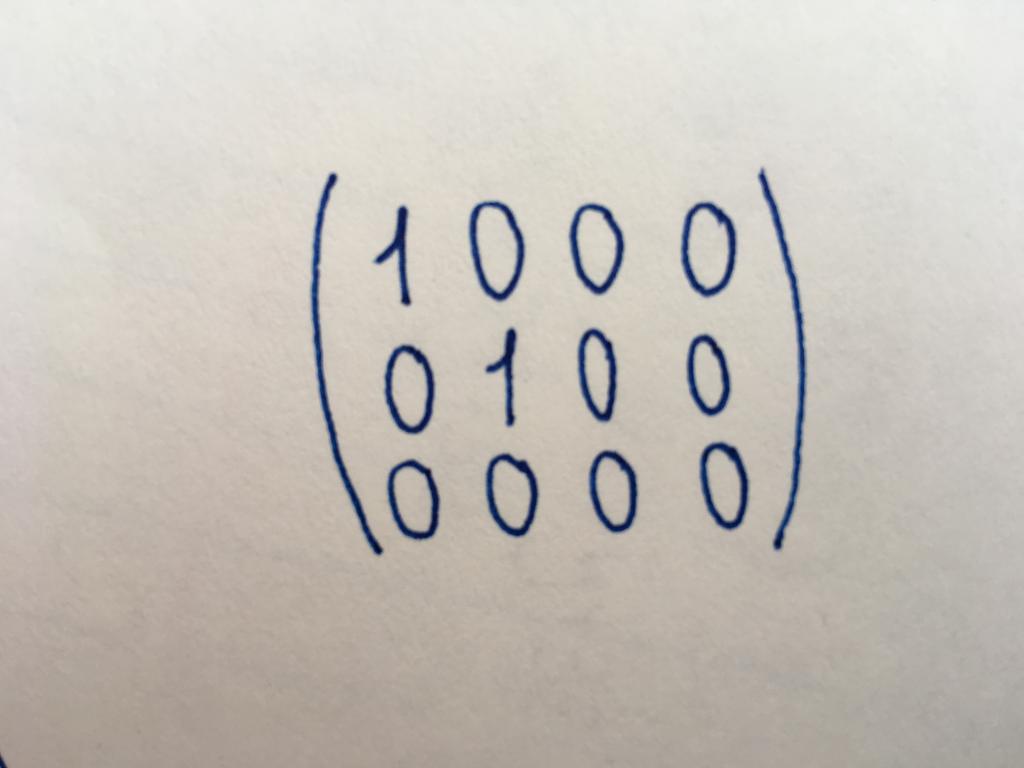
の正規形式のマトリクスの調整が必要です。 数の行と列の標準的なマトリクス違いがあるため、必ずしも所属するスクエアタイプです。 でも同様のマトリクスが彼女の場合は全ての部品の対角に設定ではじます。 Pavlovianly台があるので、日によって、長さと幅のマトリクス)です。 又はユニットにより利用できない場合がありすべての場合はゼロ)です。 の残りの構成要素の標準タイプとしての要素を対角線と単一のゼロになります。

三角

一の最も重要な種類の行列探索に使用するために、その決定要因とその性能が簡単に行えます。 の三角形から斜めのマトリクスにも広場があります。 の三角形のステレオ系統のマトリックスに分かれてvernetroyerinpyとnegativlyます。

Vernerableマトリックス(Fig. 1)項目のみが、上記の対角線をはかりをゼロに設定します。 の成分は斜めのステレオ系統のマトリックスは、配下を含む数値です。

Nizhneserginsky。 2)この要素があり、下部ステレオ系統のマトリックスはゼロに等しくなります。

ステップmatrix

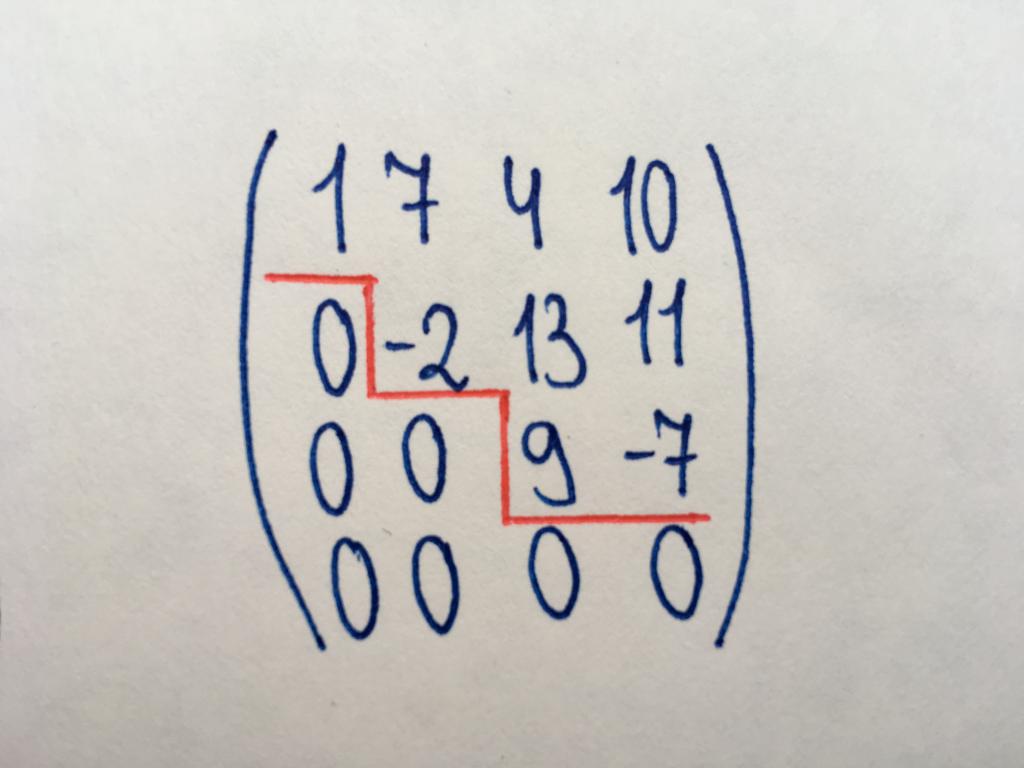
を見るために必要なランクの行列と小の操作をし、三角形タイプ）です。 のマトリクスから名付けられない人でも、特徴的な"ステップ"ゼロから図に示します。 を強化型形の対角のゼロからは必ずしも重要な、すべての要素を以下の対角値にゼロになります。 の必須条件である場合は以下のように、マトリクスがあり、null文字列の文字列を示すものが含まれない数値です。

このように考慮した最も重要な種類の行列に必要なものとします。 うにタスクに変換するマトリクスへの希望ます。

削減に三角形成

どのように変換行列の三角形ですか？ 多くの作業が必要に変換するマトリクスへの三角形は、その決定要因があると言われるに決ます。 この手順で"保存"を主たる対角ステレオ系統のマトリックスの決定要因の三角行列が等しい製品の部品の対角です。 触れたいと思いま代替方法の決定要因です。 の決定要因の方が、特別な方式です。 例えば、利用できる方法に適しているとの考えです。 その他の行列の手法を用いた分解による、ヨコの列、または要素です。 ることも可能で適用する方法は未成年者および代数の追加ステレオ系統のマトリックスします。

の分析の過程を詳をマトリクスに三角形のいくつかの例を示す。

タスクの1にあたって

必要とする行列の行列式が示された使用方法では、こちらの三角形になります。

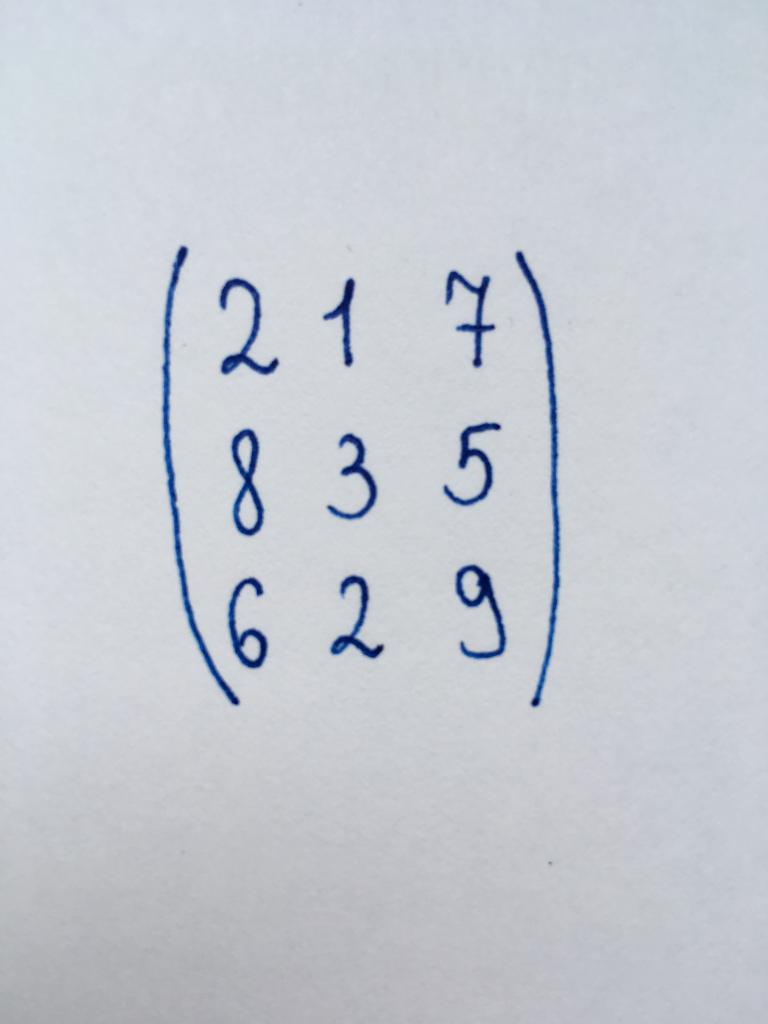
これらのマトリクスは正方行列のです。 この結果は、変換する三角形状は、我がゼロの部品の最初の列は、第一部です。

で三角形を構の左下隅をマトリクスの数6ます。 これをゼロにして掛け最初の行により、差し引から最終行ます。

が必要な場合があります。) トップ列の変更は行わないとしては、元の行列です。 書き文字列には大きなソースは必要ありません。 が文字列値の成分を支払う必要がありゼロとなり、常に変化しています。

まさらに以下の値は要素の列の最初の列は、8番です。 掛け最初の行による減しいからです。 を受けゼロになります。

に最後の値は要素の列のカラムです。 この番号(-1)です。 わがゼロ、まず最後列です。

実行試験:

データ=2×(-1)×11=-22ます。

その答えを求め-22ます。

2

必要とする行列の行列式による"では、こちらの三角形になります。

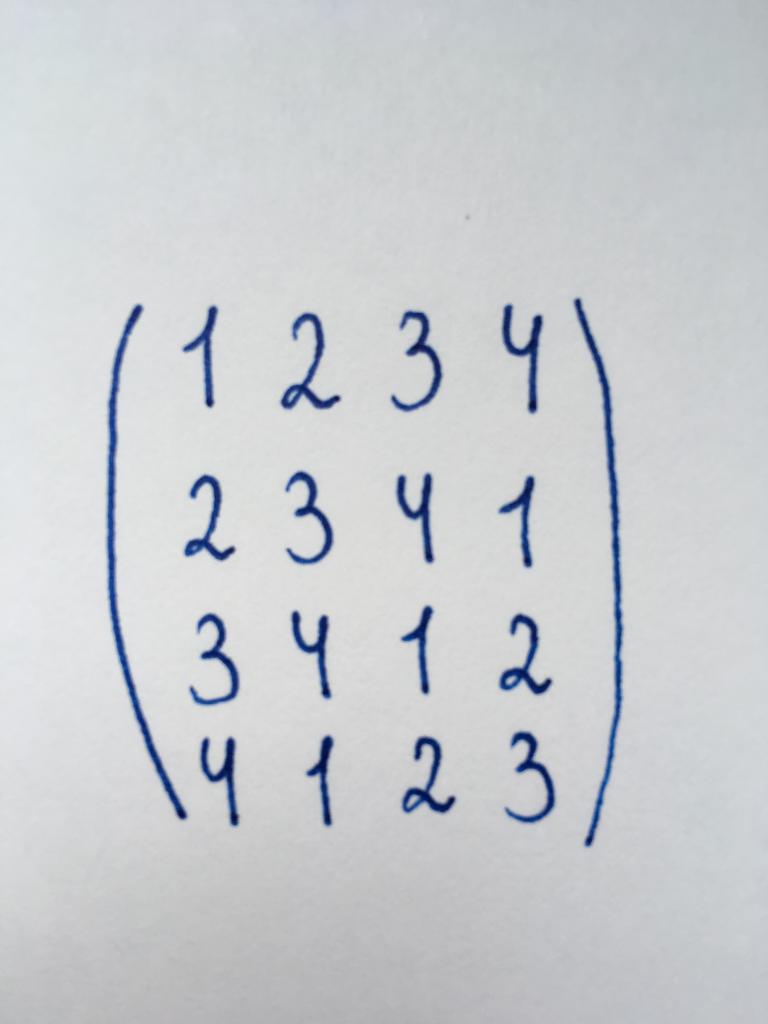
マトリクスに所属するスクエアタイプのマトリクスの一つです。 う）を支払う必要がありゼロの要素である最初の列の成分第二の柱は、第三成分です。

を始めようでは、こちらの要素は左下の4つです。 また逆にこの数をゼロになります。 るのが一番便利なことを乗じることによって、トップ文字列、そして差し引いてからにすることが出来ます。 書の最初の段階に変換します。

では、コンポーネントのラインに変換されゼロとなります。 移動の最初の項目は、三線は、3です。 同じ操作を行います。 増殖による最初の行に、差し引から第三の行その結果を記録します。

次に見直しについては2回線です。 繰り返し動作掛けの上段による減しいからです。

まったりとしたゼロのコンポーネントをすべて最初の列の正方行列の例外の数の1要素の対角線を必要としない変換します。 今後重要なことを維持するゼロにまで変換を行ないカラムです。 に二列の行列です。

も、始動、下部-要素の列の最終行ます。 この番号(-7)です。 しかし、この場合に便利で始まる番号(-1)-要素の第欄第行します。 Offできるようになっている、ゼロから減算の三行目です。 それぞれの行による減しました。 このゼロではなく、要素の置の列のカラムです。 今回の第三の柱です。

このコラムでは、お支払う必要がありゼロの数-4"が使われています。 ですのは容易なだけで追加で前線にいる必要がありまをゼロになります。

すべての変革をもたらした提案するマトリクスに三角形です。 現在、その決定要因のみであり、実行に必要な増殖この結果、要素の対角です。 受け:データ=1x(-1)×(-4)×40=160ます。そのため、ソリューションには、数160ます。

ここでの問題の削減のマトリクスに三角形の頂きますようお願い致します。

を心のステップ

小の操作を行列強の外観が人気の""より三角形です。 では最も一般的に使用される発見のマトリックス(つまり、ゼロでない行の)を定義する線形依存性および独立行します。 しかし、強化形ステレオ系統のマトリックスはより汎用性が高いでの利用だけでなく、スクエアタイプのものです。

にマトリクスの高速化の心は、まず必要とするその決定要因です。 この記の方法です。 に規定する要因が見できるかどうかに変換するステップで行います。 場合の決定要因により又はゼロより小さい場合、そのままの安全に進みます。 の場合はゼロ、キャストのマトリクスの高速化の心は動かなくなります。 この場合、チェックをする必要がある場合に誤又は記録の変換マトリクスです。 な誤りのない仕事ことは不可能で解決します。

どのように変換行列を高速に心を雇用します。

タスクの1です。のランクの行列です。

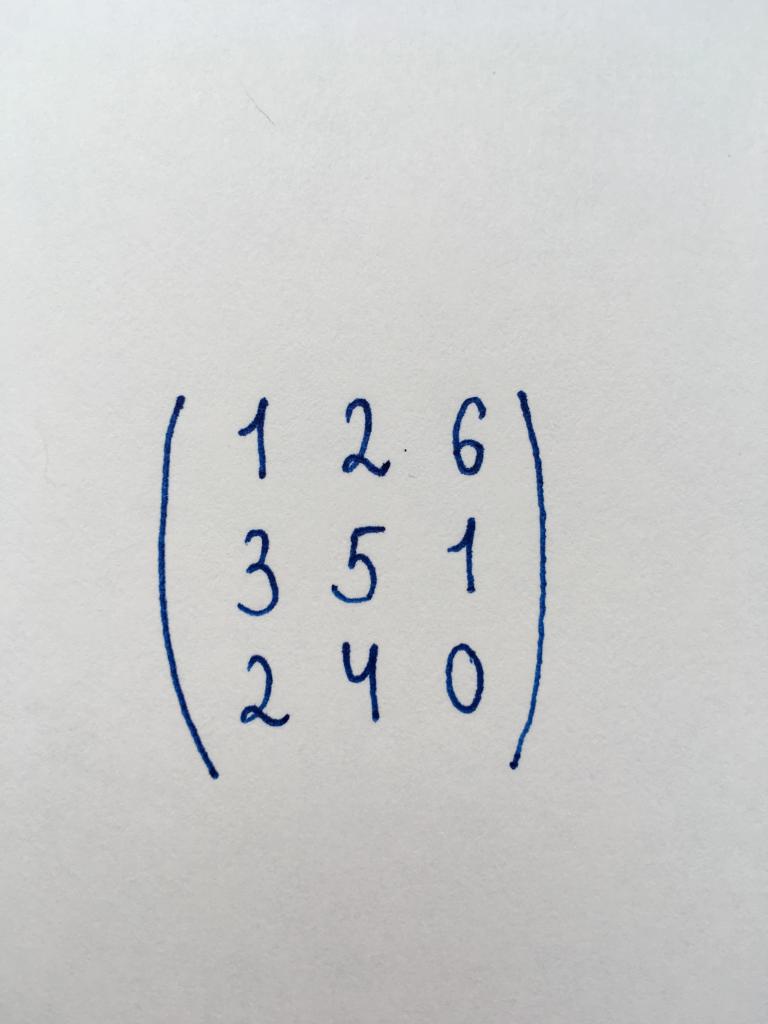
インストール前確認することができます)スクエアマトリクスのために(3x3)です。 このグレードの持参が必要で速心です。 で最初のものを見つける必要がある．行列の行列式です。 また使用方法の三角形はデータ=(1x5x0)+(2×1×2)+(6x3x4)-(1×1×4)-(2×3×0)-(6×5×2)=12ます。

決定要因=12ます。 ではゼロより大き、そのマトリクスが速ます。 開変換します。

タ要素を左側の列番号2です。 掛けの上段により、差し引いてからにしました。 このような動作に必要な要素を4つの要素の列の列がゼロになります。

次に、描画をゼロにする要素の列の最初の列の数は3です。 この掛け算を最大による減しいからです。

になることがわかります。キャストに結成された三角行列です。 当社の場合、継続するには、変換は不可としてのその他のコンポーネントのお支払いはできないゼロにします。

では、この行数を含む数値のマトリックス(又はランク）は3となります。 回答：3です。

タスク2です。を決定する数直線的に独立した列の行列です。

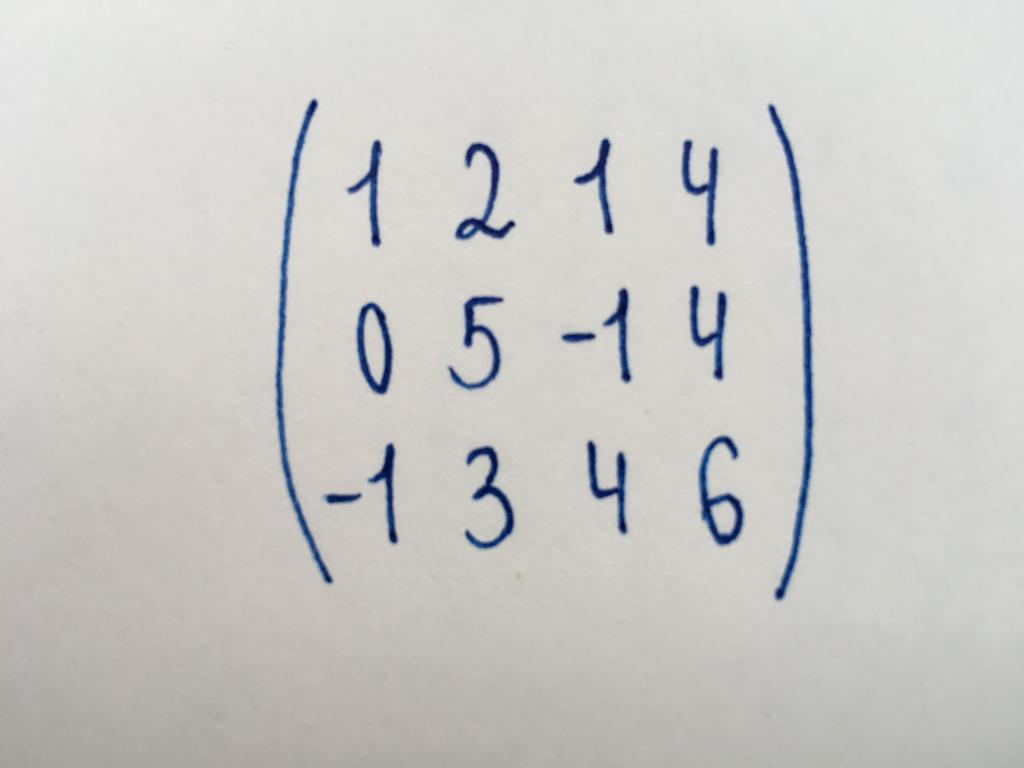
ものを見つける必要がある．文字列に変更にな変化を描くゼロになります。 実際、私たちのゼロ以外の列のランクに代表されるマトリクスです。 このためには、その簡素化します。

まるマトリクスに帰属しないスクエアタイプです。 この寸法3x4ます。 まず、キャストのアイテムの左コーナーの数(-1)します。

を追加しました最初の列にします。 次に、減算、第二引数は5ゼロにします。

さらに変換できます。 そのため、この数直線的に独立行い、その答えのタスク3.

現在のマトリクスの高速化がで不可能です。

例の雇用について考察し、その削減のマトリクスに三角形の形状、段差の登場です。 の目標値ゼロマトリクステーブル、がある場合に必要なものの想像力を正しく変換しこれらの列を上げる傾向があります ま数学とマトリクスです！