Rodzaje matryc. Stopniowy widok matrycy. Sprowadzenie macierzy do ступенчатому i треугольному myśli

Matrix - to specjalny obiekt w matematyce. Przedstawiany w formie prostokątnej lub kwadratowej tabeli, złożonego z określonej liczby wierszy i kolumn. W matematyce istnieje wiele różnych rodzajów matryc, różniących się wielkością lub treści. Numery wierszy i kolumn są nazywane procedurami. Obiekty te są używane w matematyce do porządkowania zapisu układów równań liniowych i łatwego wyszukiwania ich wyników. Równania z wykorzystaniem macierzy są rozwiązywane za pomocą metody Carla Gaussa, Gabriela Kramera, миноров algebraicznych i dodatków, a także na wiele innych sposobów. Podstawowe umiejętności w pracy z matrycami jest doprowadzenie do widoku standardowego. Jednak na początek zobaczmy, jakie rodzaje matryc podkreślają matematyki.

Zero typ

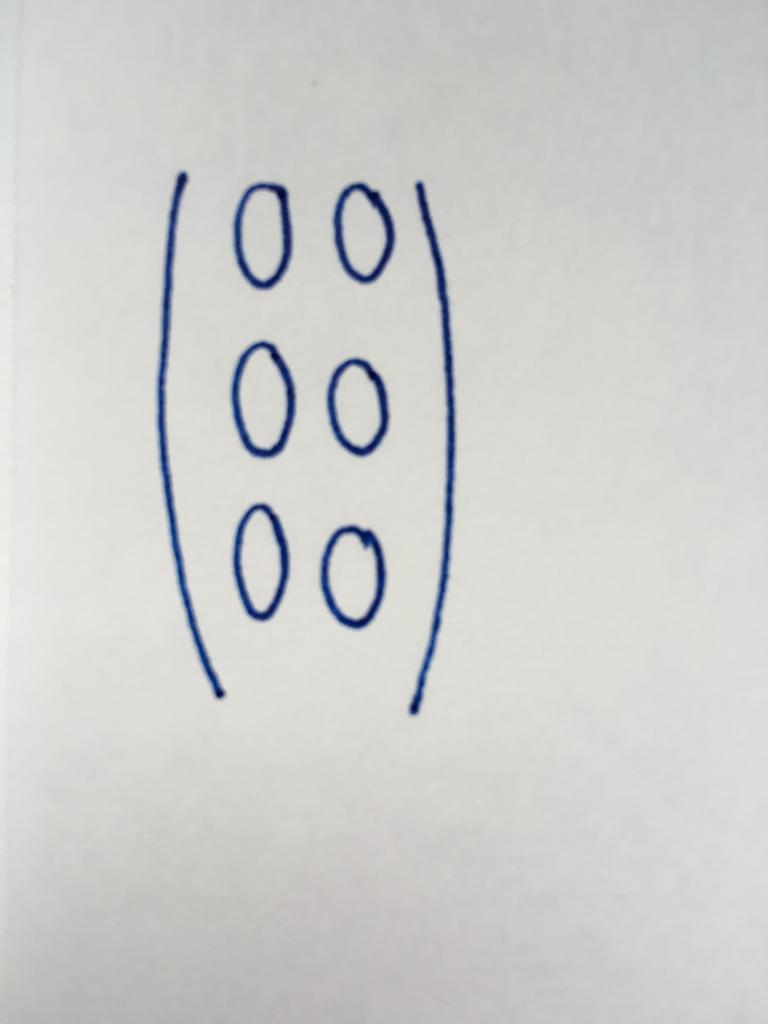
Wszystkie składniki tego rodzaju matrycy - zera. Tymczasem, liczba wierszy i kolumn jest całkowicie różny.

Kwadrat rodzaj

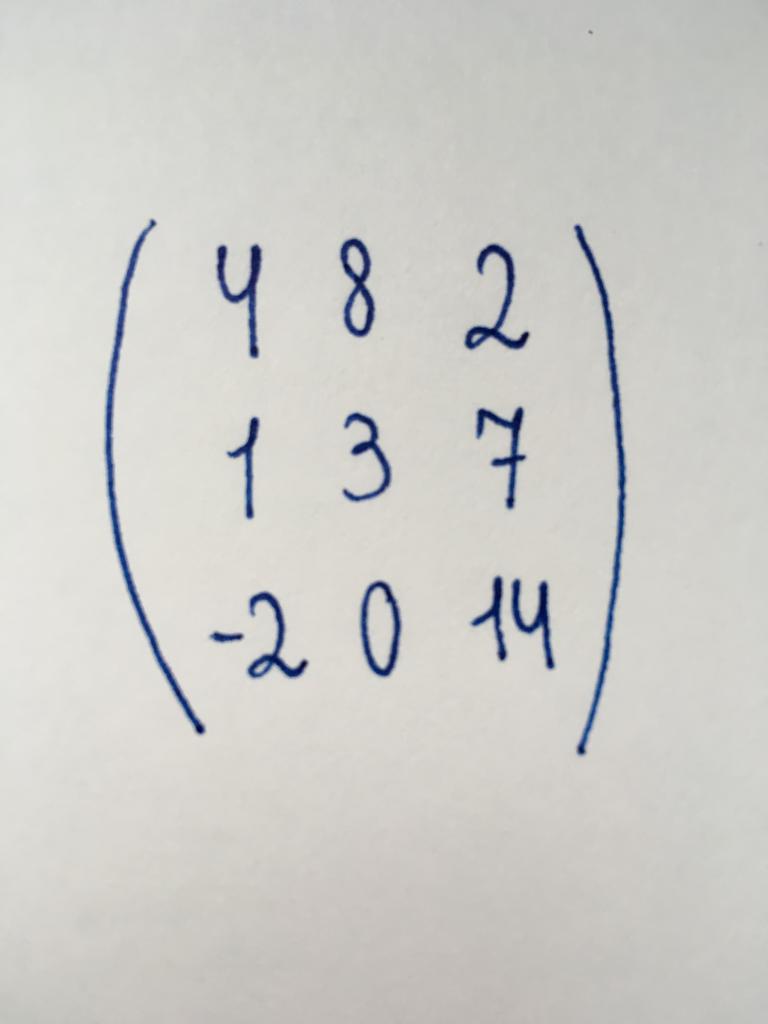
Liczba kolumn i wierszy tego rodzaju matrycy jest taka sama. Inaczej mówiąc, jest to tabela formy "kwadrat". Liczba jej kolumn (lub wierszy) nazywane są zasadami. Prywatnymi sprawami jest istnienie macierzy drugiego rzędu (macierz 2x2), czwartego rzędu (4x4), x (10x10), xvii (17x17) i tak dalej.

Wektor-стобец

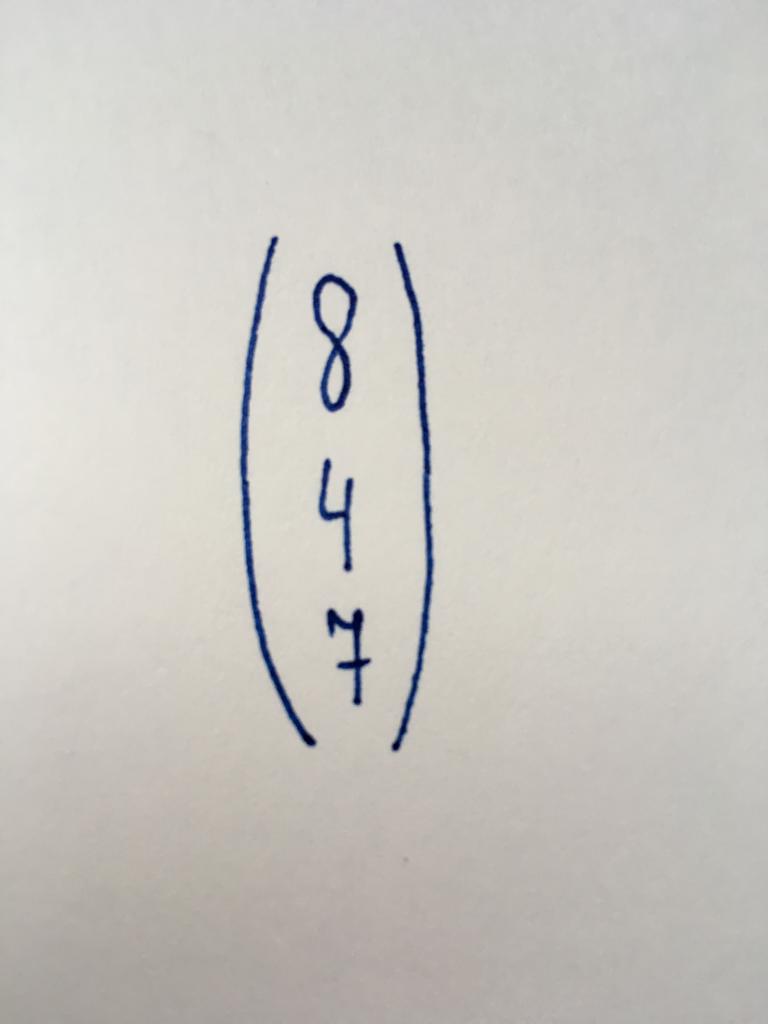
Jest To jeden z najprostszych rodzajów matryc, który zawiera tylko jedną kolumnę, która zawiera trzy wartości numeryczne. Jest wiele wolnych członków (liczb, niezależne od zmiennych) w układach równań liniowych.

Wektor-wiersz

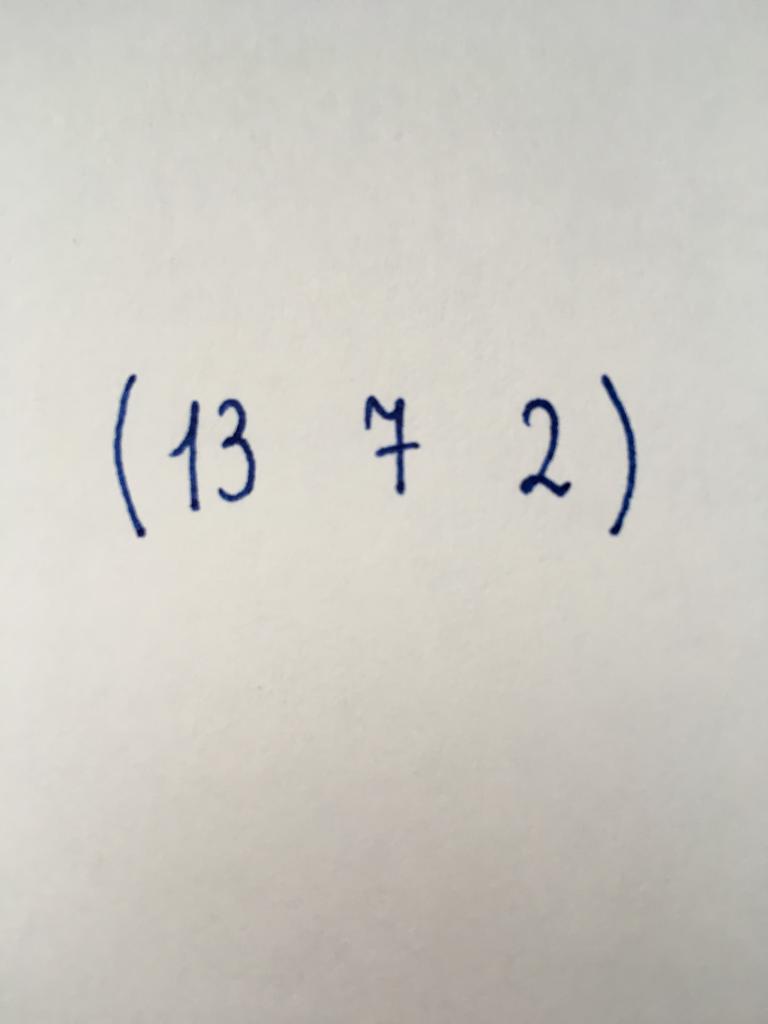
Widok podobny do poprzedniego. Składa się z trzech numerycznych elementów, z kolei zorganizowane w jeden ciąg.

Przekątnej typ

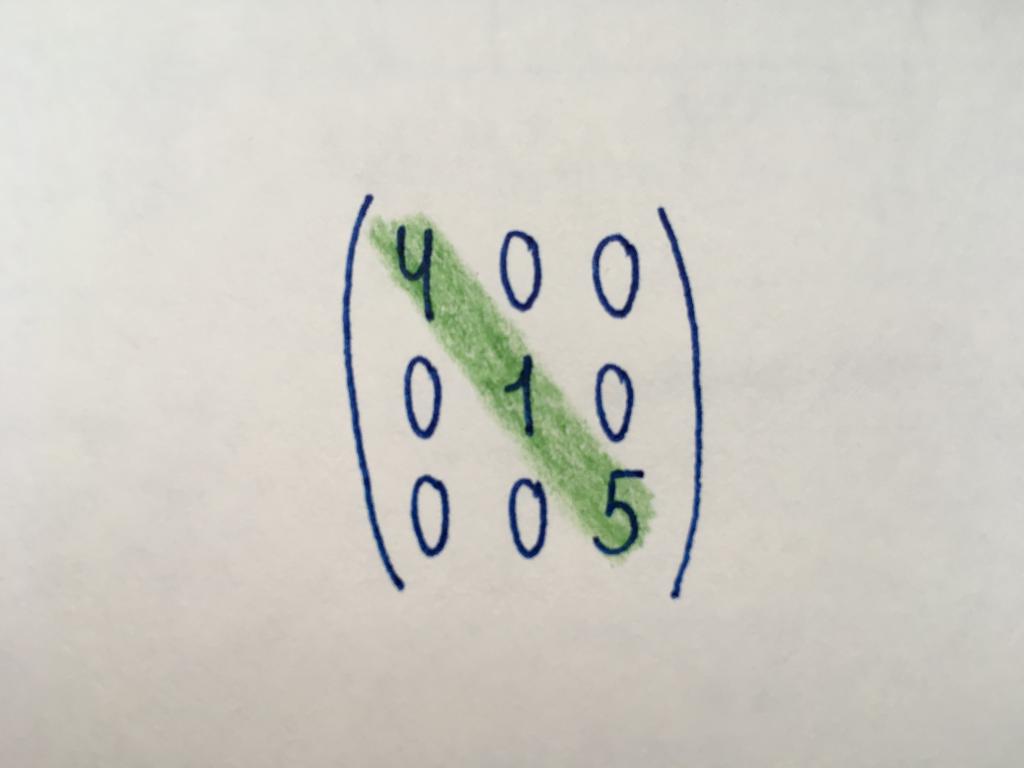
Liczbowe wartości na przekątnej macierzy przyjmują tylko elementy głównej przekątnej (zaznaczona na zielono). Podstawowe przekątna zaczyna się od elementu, znajdującego się w prawym górnym rogu, a kończy się liczbą w trzeciej kolumnie trzeciej linii. Pozostałe elementy są równe zero. Przekątnej typ jest tylko kwadratową macierz jakiegokolwiek porządku. Wśród matryc przekątnych rodzaje można wyróżnić скалярную. Wszystkie jej funkcje przyjmują te same wartości.

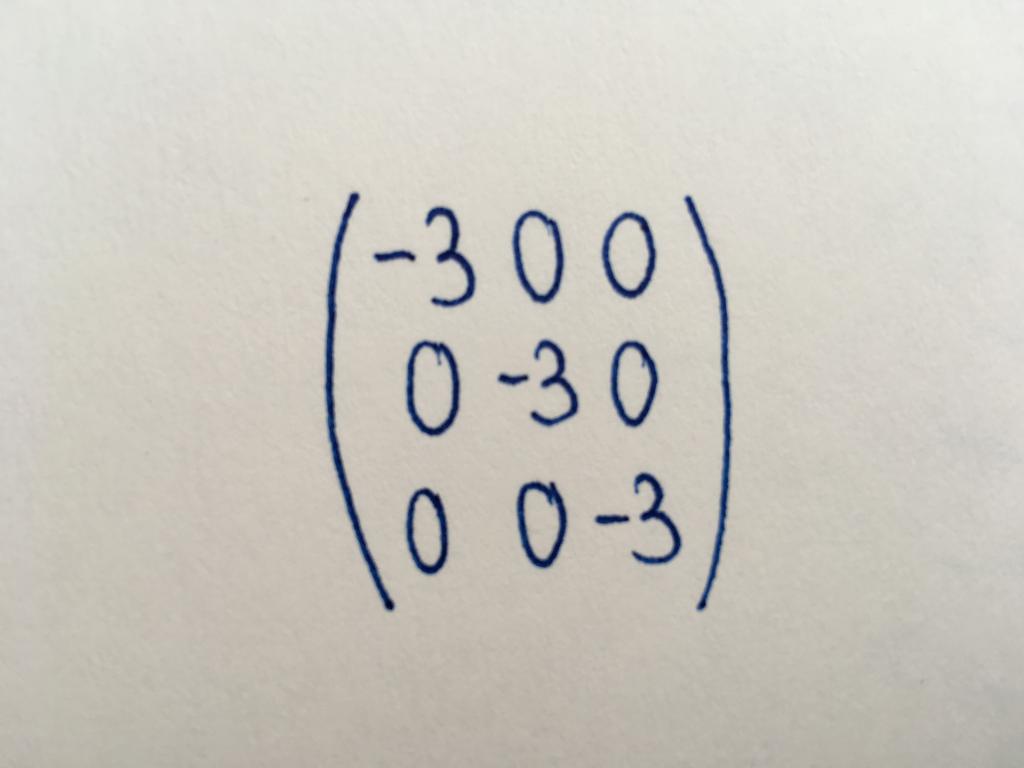
Pojedyncza matryca

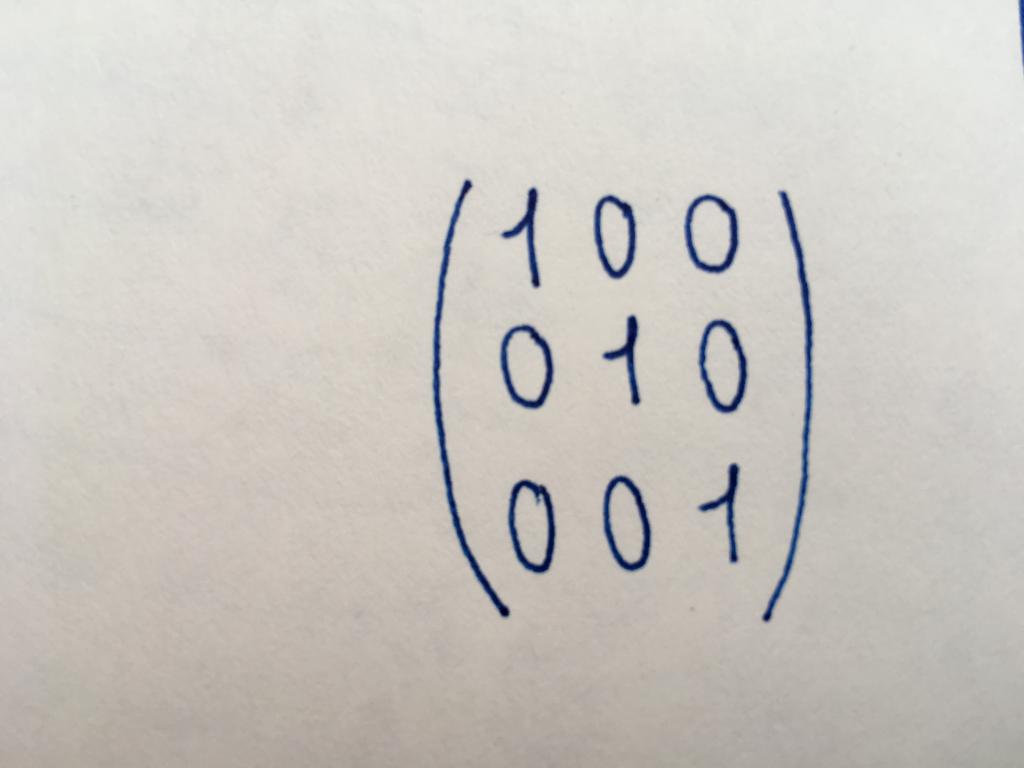
Podgatunek przekątnej matrycy. Wszystkie wartości liczbowe są jednostkami. Wykorzystując pojedynczy typ matrycy tabel, wykonują jej podstawowe konwersji lub znaleźć macierz odwrotną oryginalnej.

Kanoniczny typ

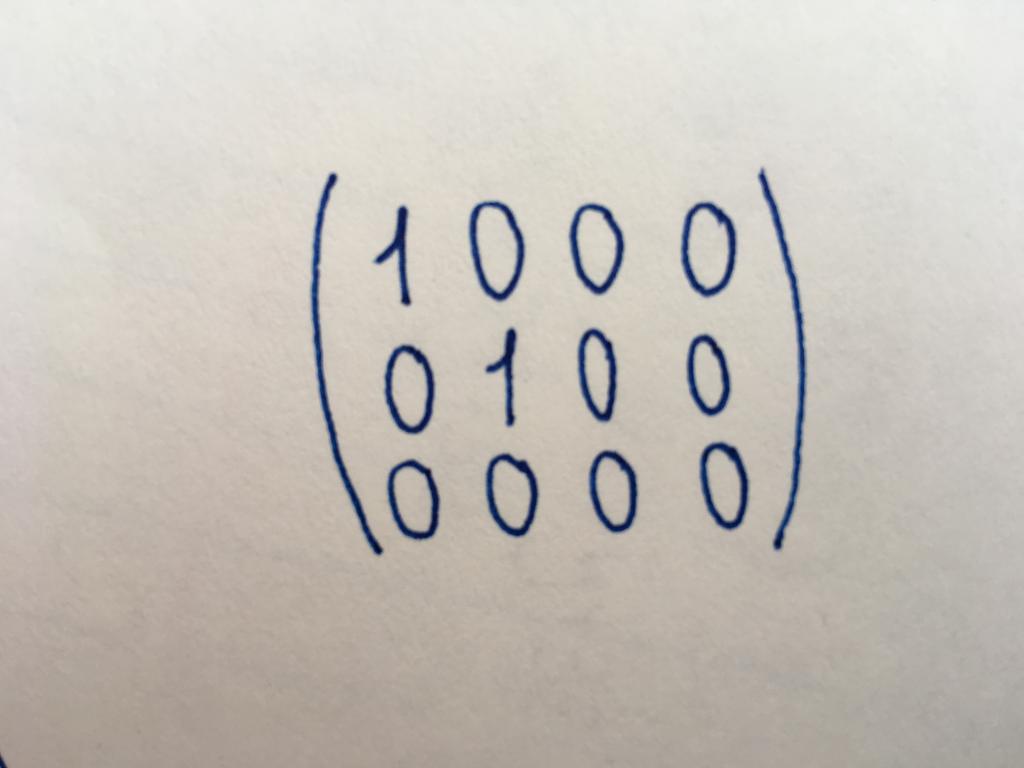
Postaci Kanonicznej macierzy jest jednym z podstawowych; doprowadzenie do niego jest często niezbędne do pracy. Liczba wierszy i kolumn w kanonicznej macierzy jest różny, nie należy do kwadratowego typu. Jest nieco podobna do pojedynczą macierz, jednak w jej przypadku nie wszystkie elementy głównej przekątnej przyjmuje wartość równą jedności. Главнодиагональных jednostek może być dwie, cztery (wszystko zależy od długości i szerokości matrycy). Lub jednostki mogą nie być w ogóle (wtedy jest ona uważana za zero). Pozostałe elementy kanonicznego rodzaju, jak i elementy oporu i pojedynczego, są równe zeru.

Urządzenie typu

Jeden z najważniejszych gatunków matrycy zastosowany w poszukiwaniu jej детерминанта i podczas wykonywania najprostszych czynności. Urządzenie typu pochodzi od kierunku ruchu, więc macierz jest kwadratowa. Trójkątny rodzaj matrycy spadają na верхнетреугольный i нижнетреугольный.

W верхнетреугольной matrycy (rys. 1) tylko te elementy, które znajdują się powyżej głównej przekątnej, przyjmuje wartość równą zero. Składniki samej przekątnej i części matrycy, rozmaitych atrakcji znajdujących się pod nią, zawierają wartości liczbowe.

W нижнетреугольной (rys. 2), natomiast elementy, które znajdują się w dolnej części matrycy, są równe zeru.

Biegowa matrix

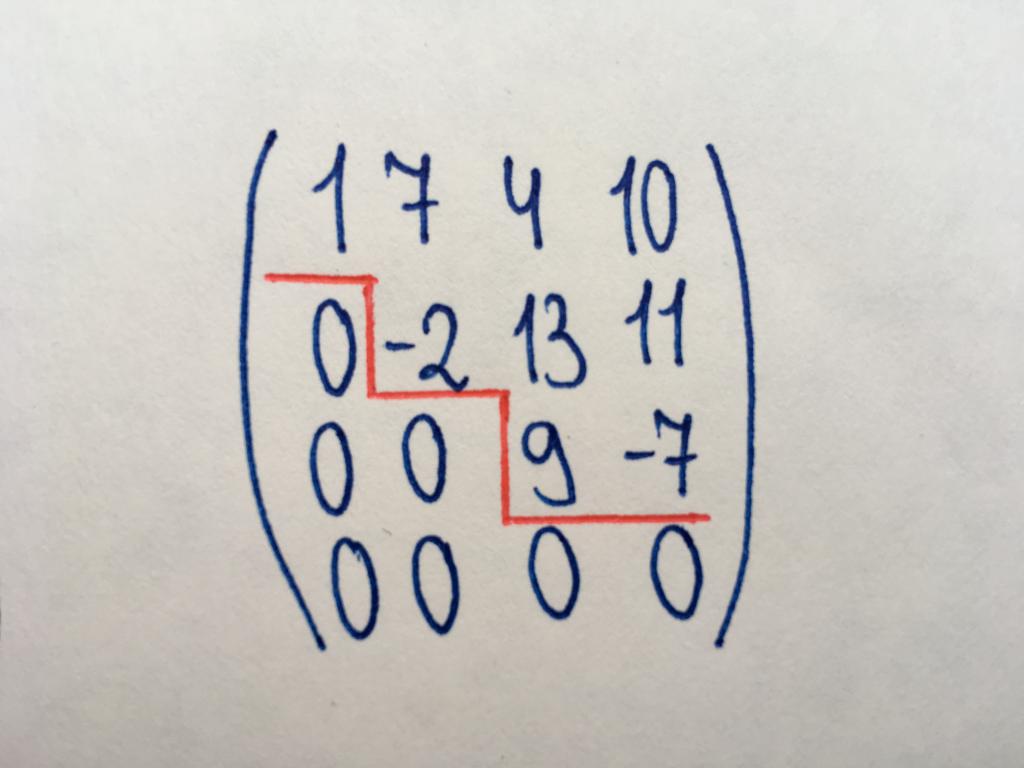
Widok jest potrzebny do znajdowania rzędu macierzy, a także dla podstawowych działań nad nimi (wraz z trójkątnym typ). Biegowa matryca została tak nazwana, ponieważ znajdują się w niej charakterystyczne "stopnie" z zer (jak pokazano na rysunku). W ступенчатом typu tworzy przekątna z zer (opcjonalnie strona główna), a wszystkie elementy pod tym przekątnej też mają wartości równe zero. Warunkiem jest następujący: jeśli w biegową matrycy jest zerowy wiersz, pozostałe wiersze znajdujące się poniżej niej, nie zawierają wartości liczbowych.

W Ten sposób omówiliśmy najważniejsze typy matryc, niezbędne do pracy z nimi. Teraz zajmiemy się zadaniem przekształcenia macierzy w żądanejformularz.

Doprowadzenie do треугольному myśli

Jak doprowadzić macierz do треугольному myśli? Najczęściej w zadaniach trzeba przekształcić macierz trójkątna widok, aby znaleźć jej determinanty, inaczej zwany wyznacznikiem. Wykonując tę procedurę, bardzo ważne jest, aby "zachować" głównej przekątnej macierzy, bo uwarunkowań trójkątny macierzy a jest równy dokładnie iloczynowi elementów jej głównej przekątnej. Przypomnę również alternatywne metody znajdowania się dostawca. Determinanty kwadratowego typu znajduje się przy pomocy specjalnych formuł. Na przykład, można skorzystać z metody trójkąta. Dla innych matryc korzystają z metody rozkładu w wierszu, kolumnie lub ich elementów. Można również zastosować metodę миноров i algebraicznych dodatków macierzy.

Szczegółowo analizuje proces dostosowania przetwornika do треугольному myśli na przykładach niektórych zadań.

Zadanie 1

Trzeba znaleźć uwarunkowań podanych macierzy, za pomocą metody doprowadzenia do треугольному myśli.

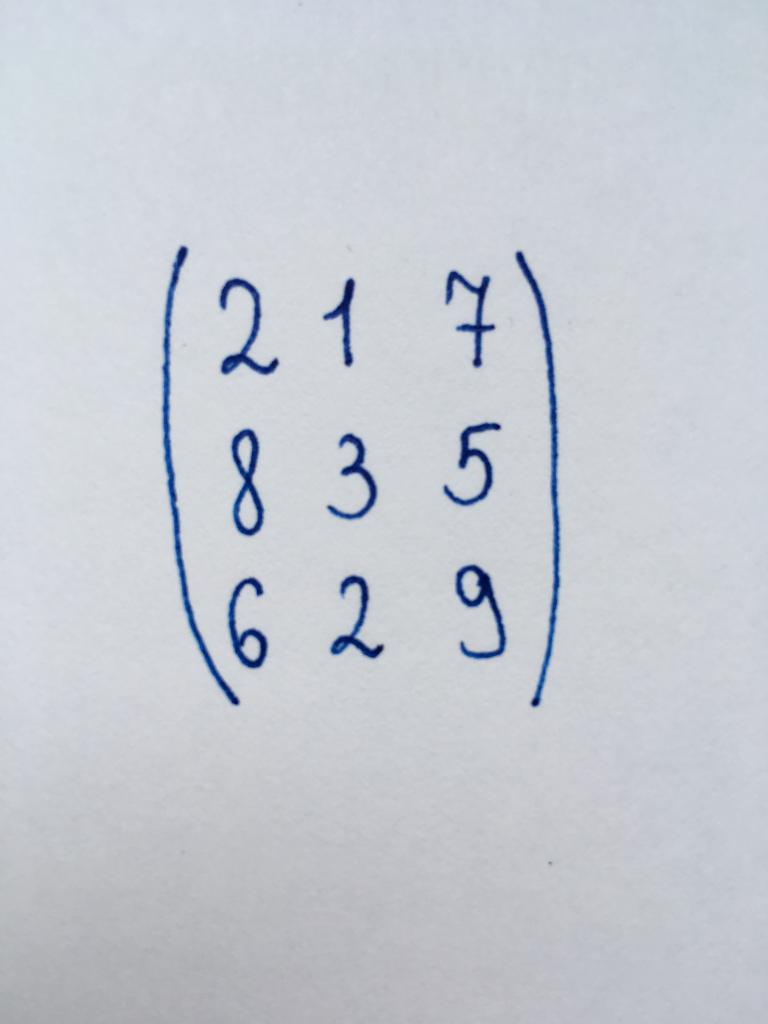
Ta nam macierz jest kwadratowa macierz trzeciego rzędu. Dlatego też w celu jej przekształcenia w trójkątny kształt, musimy zwrócić na zero dwa elementy pierwszej kolumny i jeden składnik drugiego.

Aby doprowadzić ją do треугольному pamiętać, zacznijmy konwersja z lewego dolnego rogu matrycy - z liczby 6. Aby zwrócić go do zera, należy pomnożyć pierwszy wiersz na trzy i weźmy ją z ostatniego wiersza.

Ważne! Górny wiersz nie zmienia się, a pozostaje taka sama jak w oryginalnej matrycy. Nagrywanie wiersz, cztery razy większą oryginalnej, nie trzeba. Ale wartości wierszy, elementy które trzeba zwrócić na zero, ciągle się zmienia.

Dalej zajmiemy się w następujący wartością elementem drugim wierszu pierwszej kolumny, liczby 8. Mnożenie pierwszy wiersz na cztery i weźmy ją z drugiego wiersza. Otrzymamy zero.

Jeszcze tylko ostatnia wartość - element trzeciego wiersza drugiej kolumny. To jest liczba (-1). Aby zwrócić go do zera, z pierwszego wiersza weźmy drugą.

Wykonaj test:

DetA = 2 x (-1) x 11 = -22.

To Znaczy, że odpowiedź do zadania: -22.

Zadanie 2

Trzeba znaleźć uwarunkowań macierzy metodą doprowadzenia do треугольному myśli.

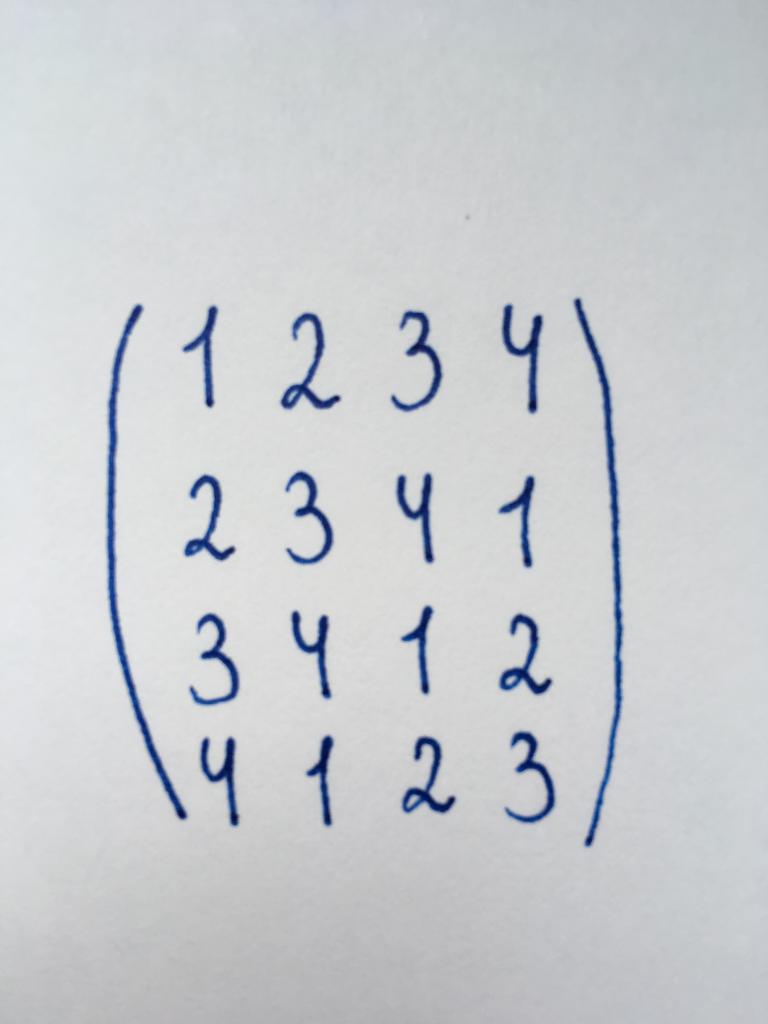
Przedstawione matryca należy do kwadratowego typu i jest macierzą czwartego rzędu. To znaczy, że należy zwrócić na zero trzy elementy pierwszej kolumny, dwa elementy drugiej kolumny i jeden składnik trzeciego.

Zacznijmy doprowadzenie jej z elementu, znajdującego się w lewym dolnym rogu, - z liczby 4. Musimy zwrócić tę liczbę do zera. Najłatwiej zrobić to, mnożąc na cztery górną linię, a następnie odjąć ją z czwartego. Piszemy podsumowanie pierwszego etapu transformacji.

Tak Więc, składnik czwartego wiersza nawrócił się na zero. Przejdź do pierwszego elementu trzeciego wiersza, do liczby 3. Wykonujemy podobną operację. Pomnożyć przez trzy pierwszą linię, odejmujemy ją z trzeciego wiersza i zapisujemy wynik.

Dalej widzimy liczbę 2 w drugim wierszu. Powtarzamy operację: pomnóż górny wiersz na dwa i odejmujemy ją od drugiej.

Udało Nam się zwrócić do zera wszystkie elementy pierwszej kolumny tej macierzy kwadratowej, za wyjątkiem liczby 1 - elementu głównej przekątnej, nie wymaga konwersji. Teraz ważne jest, aby zachować otrzymane zera, więc będziemy wykonywać konwersji z wierszami, a nie z kolumnami. Przejdźmy do drugiej kolumny przedstawionej macierzy.

Znowu zaczynamy od dołu - z pozycji drugiej kolumnie ostatniego wiersza. Jest to liczba (-7). Jednak w tym przypadku wygodniej jest zacząć od liczby (-1) - element drugiej kolumny trzeciej linii. Aby zwrócić go do zera, weźmy z trzeciego wiersza drugiego. Następnie należy pomnożyć drugi wiersz na siedem i weźmy ją z czwartego. Mamy zero zamiast elementu, znajdującego się w czwartym wierszu drugiej kolumny. Teraz przejdźmy do trzeciej kolumny.

W tej kolumnie musimy zwrócić na zero tylko jedną liczbę - 4. To nie jest trudne: wystarczy dodawać do ostatniej linii trzecią i widzimy potrzebny nam zero.

Po wszystkich wyprodukowanych transformacji przyniosły zaproponowany przez matrycę do треугольному myśli. Teraz, aby znaleźć jej determinanty, trzeba tylko wykonać mnożenie получившихся elementów głównej przekątnej. Otrzymujemy: DetA = 1 x (-1) x (-4) x 40 = 160. Zatem rozwiązaniem jest liczba 160.

Teraz pytanie dostosowania przetwornika do треугольному myśli to nie problem.

Doprowadzenie do ступенчатому myśli

Przy podstawowych operacjach nad matrycami stopniowy widok jest mniej "popularne", niż trójkątny. Najczęściej jest on używany do znajdowania rzędu macierzy (czyli liczby niezerowych wierszy) lub do określenia liniowo zależnych i niezależnych wierszy. Jednak stopniowy widok matrycy jest bardziej uniwersalny, ponieważ pasuje nie tylko do kwadratowego rodzaju, ale i dla wszystkich innych.

Aby doprowadzić macierz do ступенчатому pamiętać, najpierw trzeba znaleźć jej determinanty. Do tego podejdą wyżej wymienione metody. Celem znalezienia детерминанта jest taka: dowiedzieć się, czy można przekształcić ją w stopniowy widok matrycy. Jeśli uwarunkowań większa lub mniejsza od zera, to można spokojnie przystąpić do zadania. Jeśli jest on równy zero, wykonać doprowadzenie macierzy do ступенчатому myśli się nie uda. W takim przypadku trzeba sprawdzić, czy nie ma błędów w zapisie lub w przemianach matrycy. Jeśli takie nieścisłości nie, zadanierozwiązać nie można.

Przyjrzyjmy się, jak doprowadzić macierz do ступенчатому myśli na przykładach wielu zadań.

Zadanie 1. Znaleźć rangę tej macierzy tabeli.

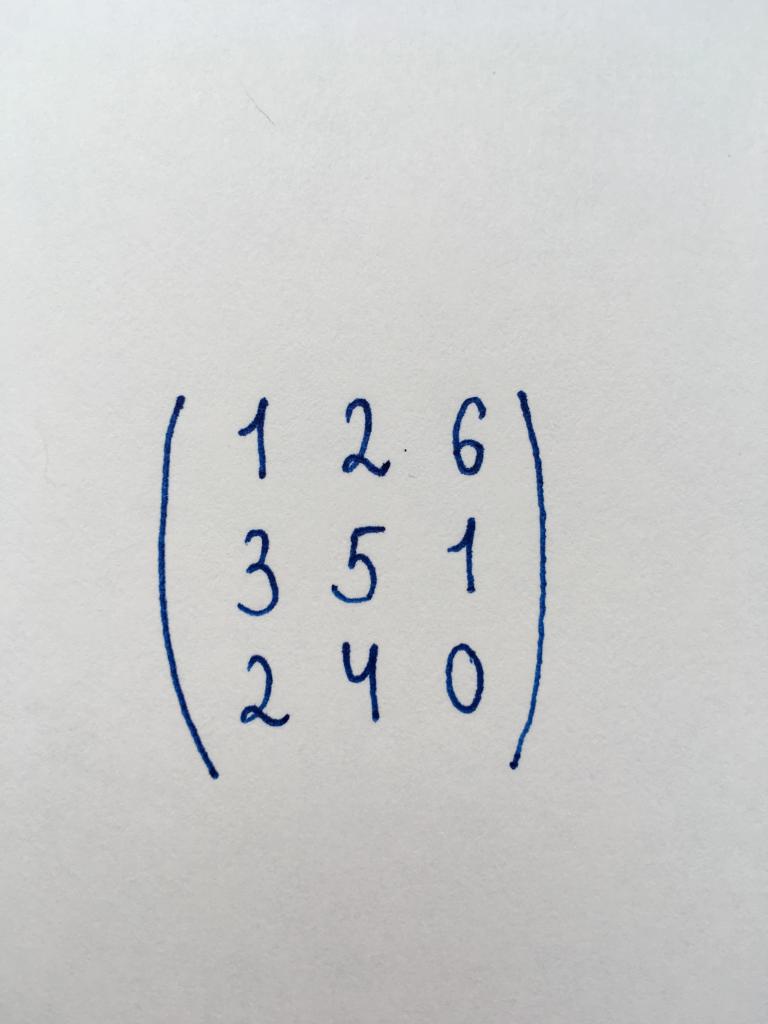
Przed nami kwadratowa macierz trzeciego rzędu (3x3). Wiemy, że w celu znalezienia rangi należy doprowadzić ją do ступенчатому myśli. Dlatego najpierw musimy znaleźć uwarunkowań matrycy. Wykorzystamy metodą trójkąta: DetA = (1 x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) - (1 x 1 x 4) - (2 x 3 x 0) - (6 x 5 x 2) = 12.

Uwarunkowań = 12. Jest większy od zera, oznacza to, że macierz można doprowadzić do ступенчатому myśli. Przystępujemy do jej zmiany.

Zacznijmy go z elementu lewej kolumnie trzeciej linii - liczby 2. Pomnóż górny wiersz na dwa i odejmujemy ją z trzeciej. Dzięki tej operacji jak żądany element, jak i liczba 4 - element drugiej kolumny trzeciej linii - zwrócił się do zera.

Następnie należy zwrócić na zero element w drugim wierszu pierwszej kolumny - liczba 3. Do tego pomnóż górną linię na trzy i odejmujemy ją od drugiej.

Widzimy, że w wyniku rzutowania powstała macierz trójkątna. W naszym przypadku kontynuować konwersję nie można, tak jak pozostałe elementy nie uda się zwrócić do zera.

To Znaczy, możemy stwierdzić, że ilość wierszy zawierających wartości liczbowe, w tym matrycy (lub jej stopień) - 3. Odpowiedź do zadania: 3.

Zadanie 2. Określić liczbę liniowo niezależnych wierszy tej macierzy.

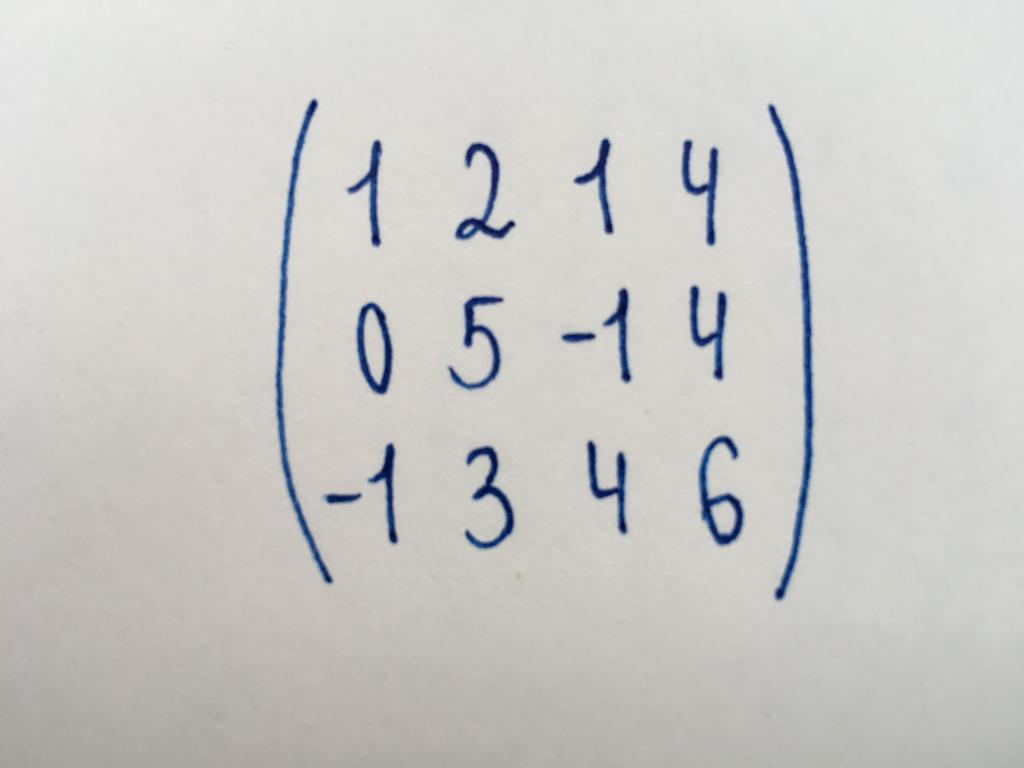
Musimy znaleźć takie wiersze, których nie można żadnymi przekształceniami zwrócić zero. W rzeczywistości musimy znaleźć liczba niezerowych wierszy, lub stopień przedstawionej macierzy. Do tego dokonamy jej uproszczenie.

Widzimy matrycę, która nie należy do kwadratowego typu. Ona ma wymiary 3x4. Zacznijmy doprowadzenie również z pozycji lewego dolnego rogu - liczby (-1).

- Dostosowujemy pierwszy wiersz do trzeciej. Dalej odejmujemy z niej drugą, aby zwrócić liczba 5 do zera.

Dalsze jej przekształcenie nie jest możliwe. To znaczy, możemy stwierdzić, że liczba liniowo niezależnych wierszy w niej i odpowiedź do zadania - 3.

Teraz sprowadzenie macierzy do ступенчатому rodzaju nie jest dla ciebie niewykonalnym zadaniem.

Na przykładach danych zadań zdemontowaliśmy sprowadzenie macierzy do треугольному myśli i ступенчатому myśli. Aby zwrócić na zero wartości macierzy tabel, w niektórych przypadkach może być konieczne, aby pokazać wyobraźnię i poprawnie je konwertować kolumny lub wiersza. Życzę sukcesów w matematyce i w pracy z matrycami!