Arten von Matrizen. Stufen-Matrix-Ansicht. Die Anführung der Matrix zu stufigen Verstärkungseinstellung und der dreieckigen Auge
Die Matrix ist ein besonderes Objekt in der Mathematik. Dargestellt in Form eines rechteckigen oder quadratischen Tisch, komponiert aus einer bestimmten Anzahl von Zeilen und Spalten. In der Mathematik gibt es eine Vielzahl von Matrizen unterschiedlicher Größe oder Inhalt. Die Anzahl der in Zeilen und Spalten heißen die Größenordnungen. Diese Objekte werden in der Mathematik für die schreibreihenfolge linearer Gleichungssysteme und einfache Suche Ihrer Ergebnisse. Gleichungen mit Hilfe der Matrix gelöst werden mittels einer Methode von Carl Gauß, Gabriel Cramer, миноров und algebraischen Ergänzungen, sowie vielen anderen Arten. Grundlegende Fähigkeit beim Umgang mit Matrizen ist es zur klassischen Ansicht. Aber zuerst wollen wir verstehen, welche Arten von Matrizen Mathematik absondern.
Null Typ
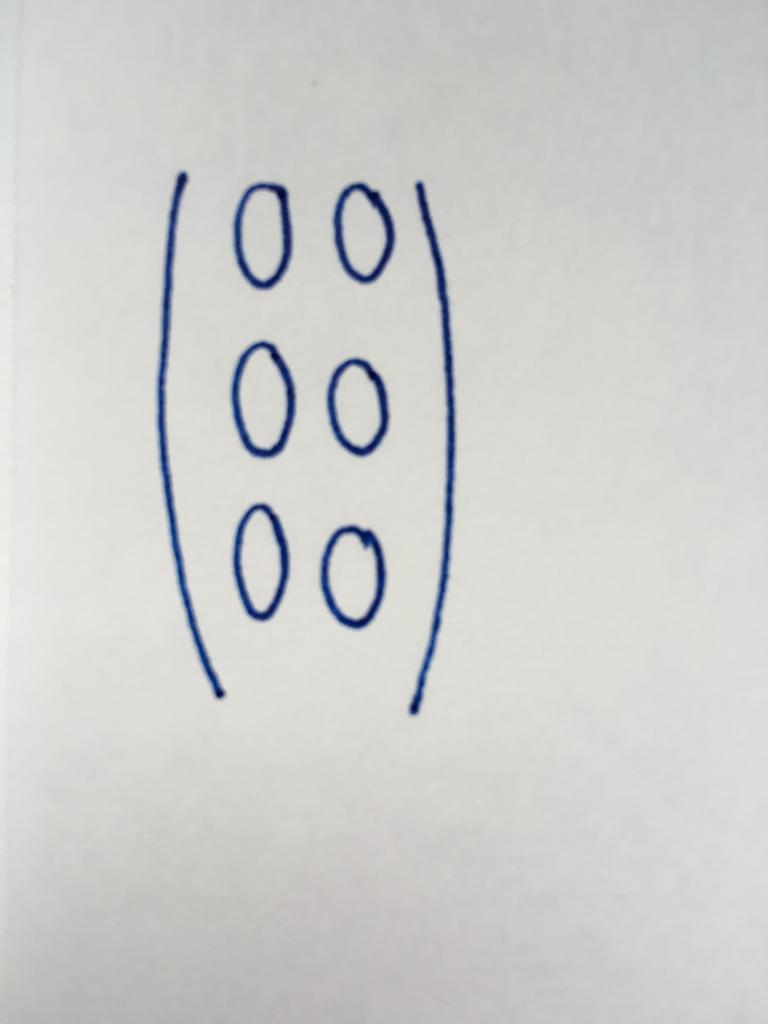
Alle Komponenten dieser Art von Matrix - Nullen. Inzwischen ist die Anzahl der Zeilen und Spalten absolut Verschieden.
Quadratisch
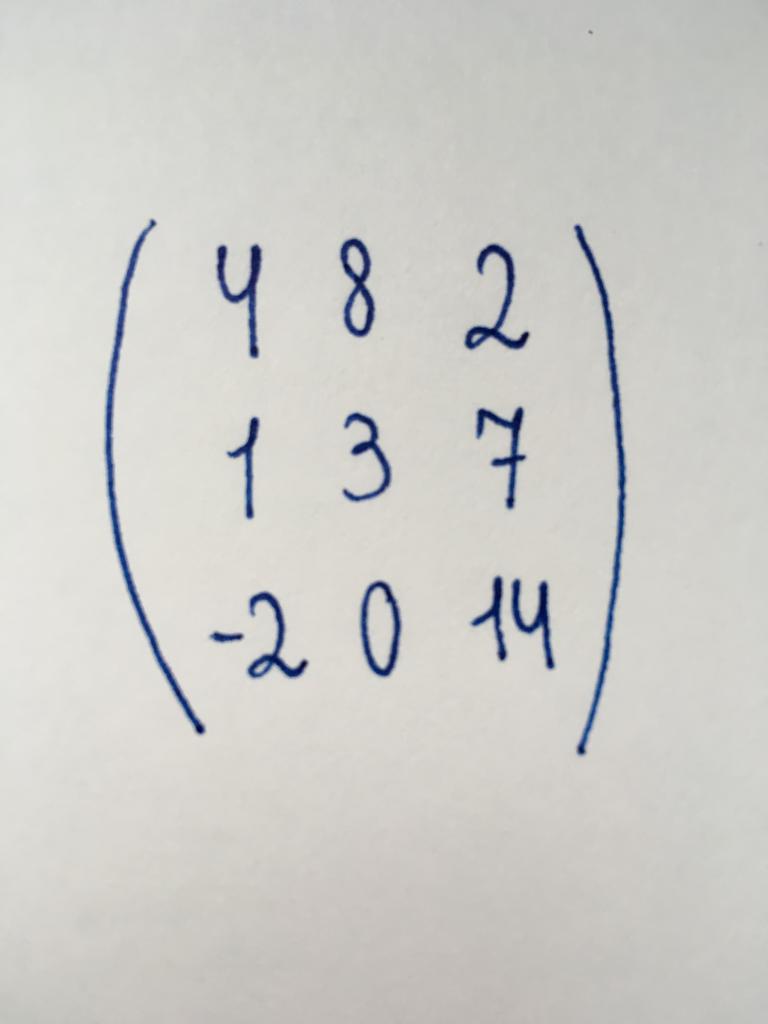
Die Anzahl der Spalten und Zeilen dieser Art der Matrix übereinstimmt. Anders gesagt, es ist eine Tabelle der Form "Quadrat". Die Anzahl der Spalten (oder Zeilen) heißen die Reihenfolge. Sonderfälle gilt als die Existenz der Matrix der zweiten Ordnung (Matrix 2x2), vierter Ordnung (4x4), zehnten (10x10), siebzehnte (17x17) und so weiter.
Vektor-стобец
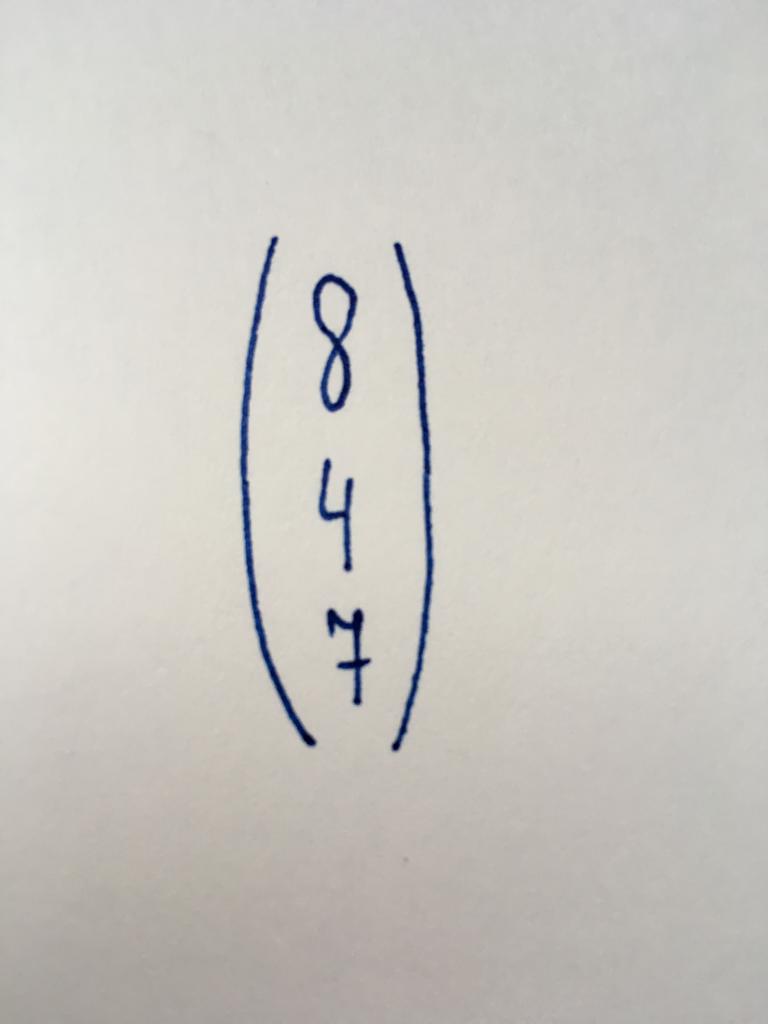
Dies ist eine der einfachsten Arten von Matrizen mit nur einer Spalte, die enthält drei numerische Werte. Es stellt eine Reihe von freien Mitgliedern (zahlen, von unabhängigen Variablen) in den Systemen von linearen Gleichungen.
Vektor-String
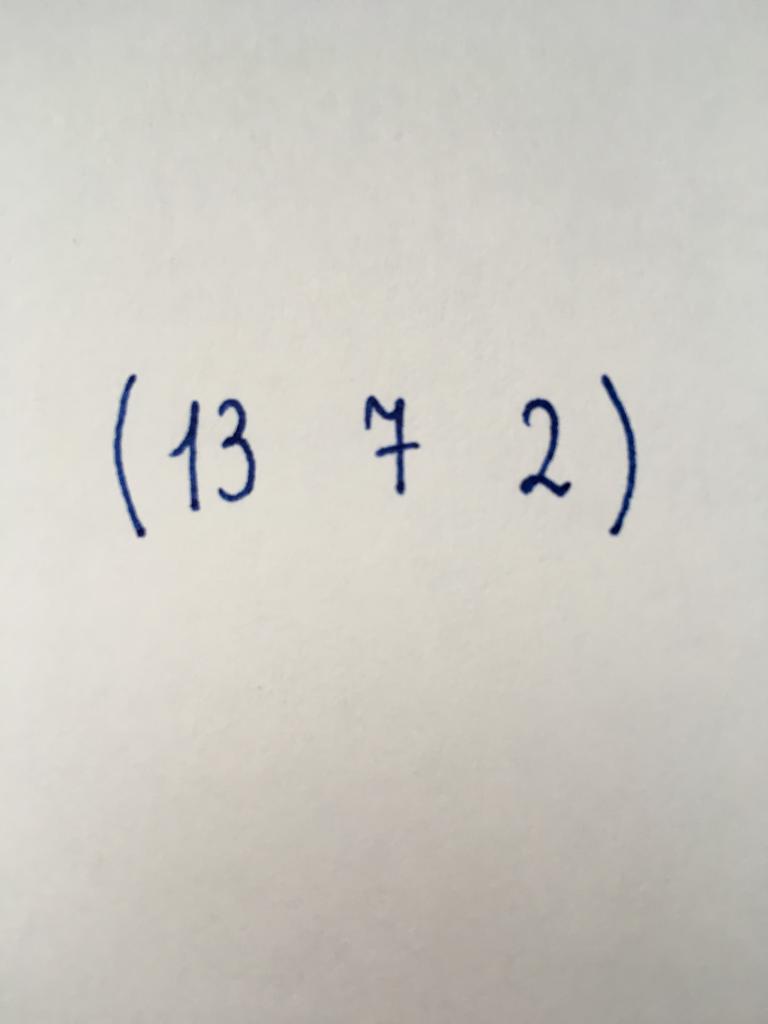
Aussehen ähnlich dem vorherigen. Besteht aus drei numerischen Elemente, wiederum organisiert in eine Zeile.
Diagonale Typ
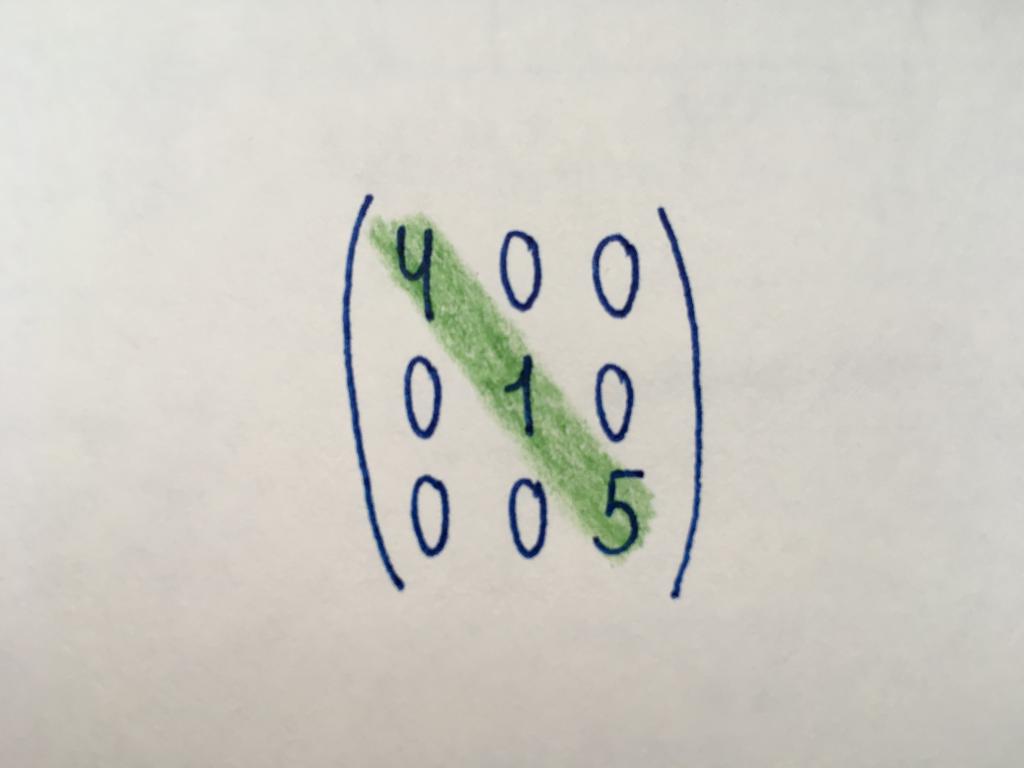
Numerische Werte in der diagonalen der Matrix nehmen nur die Komponenten der diagonalen (grün markiert). Die grundlegende Diagonale beginnt mit dem Element, das sich in der rechten oberen Ecke und endet mit der Zahl in der Dritten Spalte der Dritten Zeile. Die restlichen Komponenten sind gleich null. Diagonale Art stellt nur eine quadratische Matrix um. Unter den diagonalen Matrizen Arten Skalare unterscheiden können. Alle Komponenten identische Werte.
Mehr:
Das Deutsche Flugzeug "Messerschmitt-262": die Geschichte der Entstehung, Merkmale, Foto
High-Speed-Strahltriebwerk-Kämpfer-Abfangjäger Messerschmitt ME-262 Schwalbe („Messerschmitt ME-262 Schwalbe») erschien auf dem Schlachtfeld nur im Jahr 1944. Man kann nicht genau sagen, für welchen Job diese Maschine bestimmt. Experiment...
Moderne Schule: Geschichte, Voraussetzungen, Probleme. Modelle der modernen Schulen
Historische Entstehung von Schulen förderte den Wunsch der Menschen die Welt zu erkennen und erweitern Ihre Kenntnisse. Deshalb versucht der Mensch zur Gemeinschaft mit den weisen und sehnte sich danach von Ihnen zu lernen wissen.die Geschichte der m...
"Haare zu Berge": Bedeutung, Herkunft фразеологизма
In der Russischen Sprache treffen eine ausreichende Anzahl von geheimnisvollen Floskeln, über deren Bedeutung schwer zu erraten. Die sprachliche Konstruktion „die Haare» gehört eindeutig zu den solchen. Zum Glück, der Ursprung dieses Ausd...
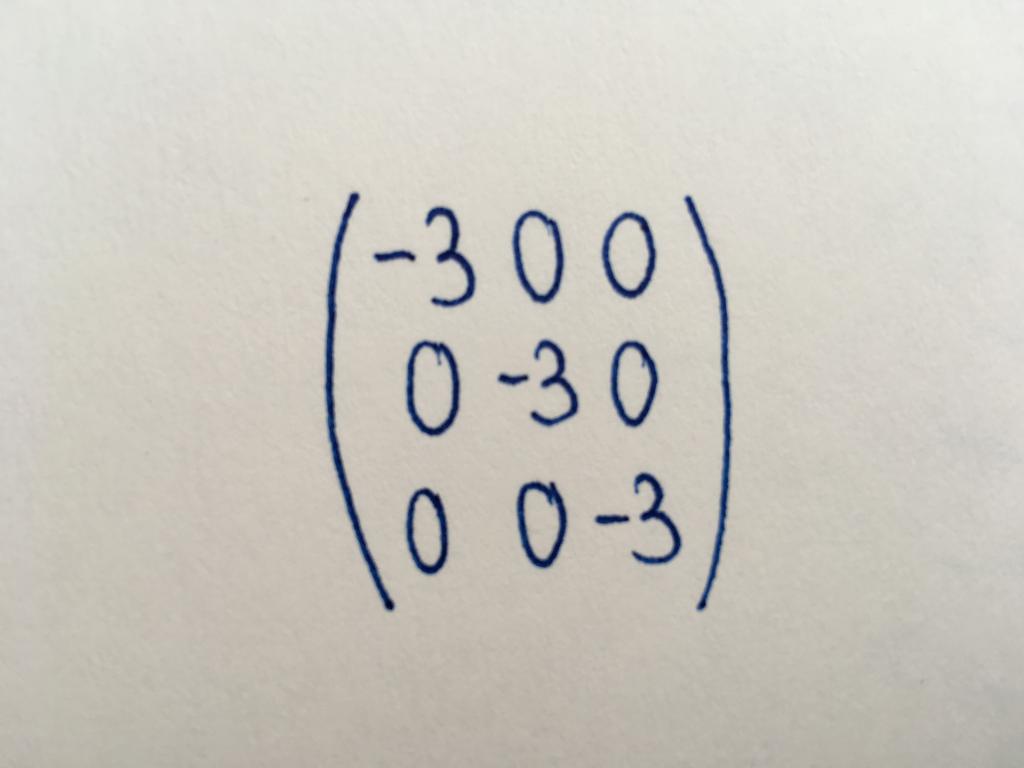
Die Einheitsmatrix
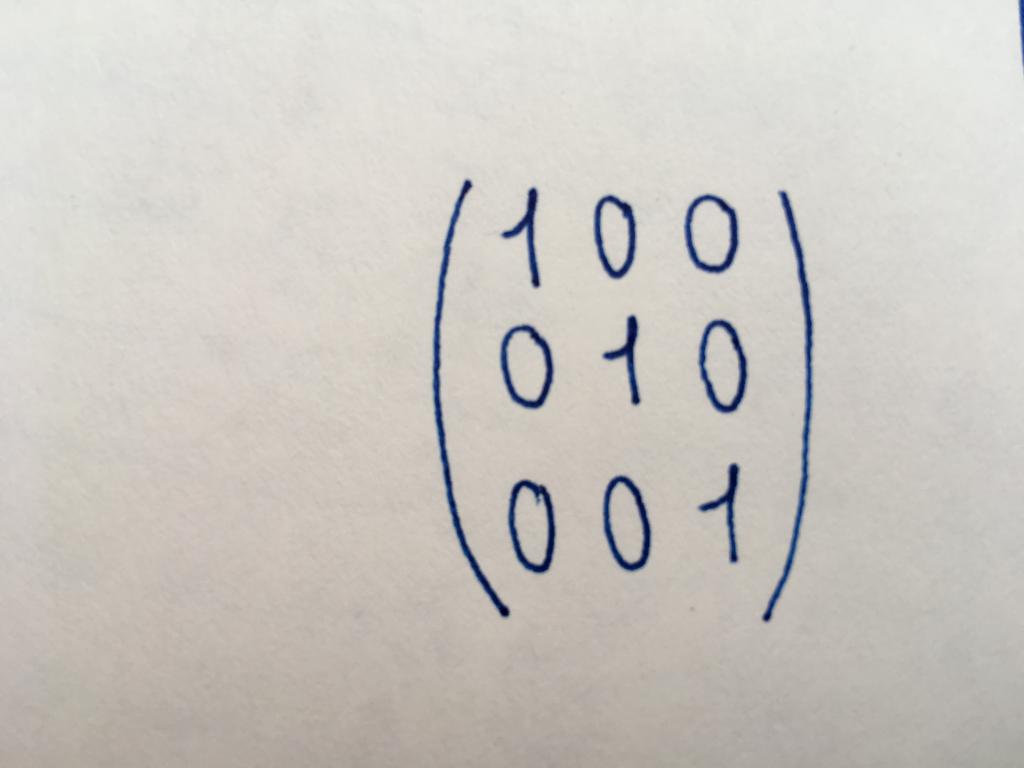
Eine Unterart der diagonalen der Matrix. Alle numerischen Werte sind die Einheiten. Mit einem einzigen Typ Matrix-Tabellen, führen Sie grundlegende Umwandlung oder finden eine Matrix, die inverse der ursprünglichen.
Kanonische Art
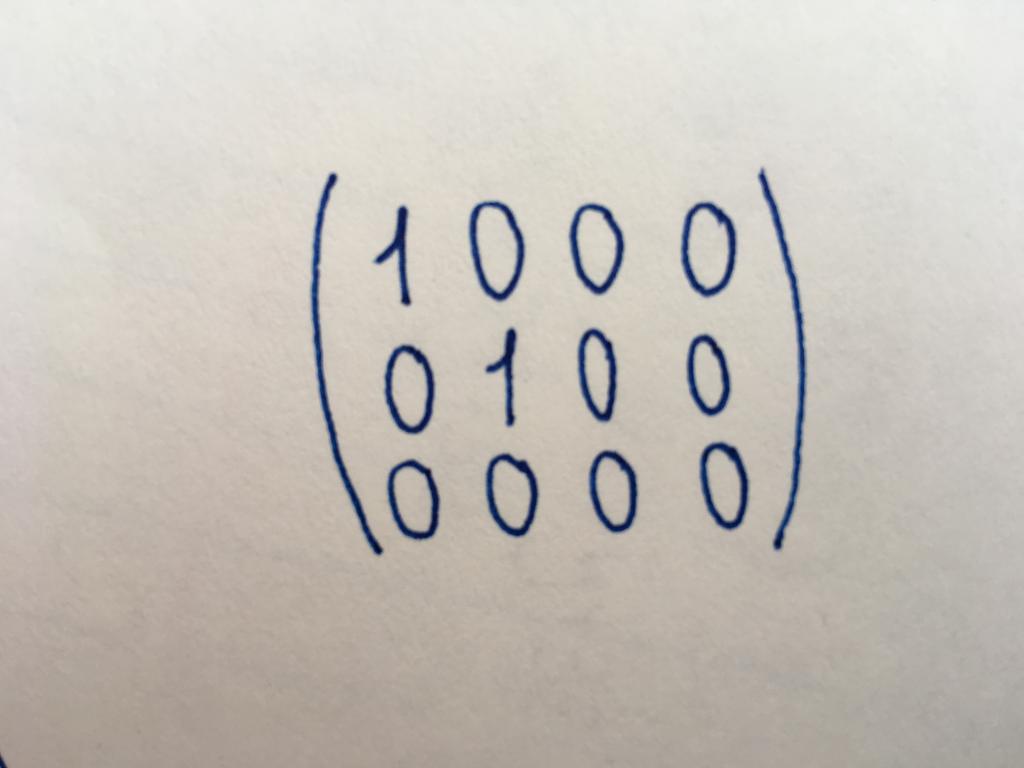
Eine Kanonische Form der Matrix gilt als einer der wichtigsten; bringt ihn oft notwendig für die Arbeit. Die Anzahl der Zeilen und Spalten der kanonischen Matrix Verschieden, es nicht gehört zu den quadratischen Typ. Es ist etwas ähnlich wie eine einzelne Matrix, aber in Ihrem Fall nicht alle Komponenten der Hauptdiagonale nehmen, während der Wert eins. Главнодиагональных Einheiten kann zwei, vier (alles hängt von der Länge und Breite der Matrix). Oder Einheiten können nicht vorhanden sein überhaupt (dann gilt es als null). Die übrigen Komponenten des kanonischen Typs, wie die Elemente der diagonalen und der einzelnen, gleich null.
Dreieckige Typ
Eine der wichtigsten Arten von Matrizen, die bei der Suche nach Ihrer Determinante und bei der Ausführung der elementaroperationen. Der dreieckige Typ kommt von der diagonalen, also die Matrix ist auch quadratisch. Dreieckige Matrix-Ansicht unterteilen auf верхнетреугольный und нижнетреугольный.

In верхнетреугольной Matrix (Abb. 1) nur Elemente, die über der Hauptdiagonalen, nehmen den Wert null. Die Komponenten der diagonalen und Teile der Matrix, darunter liegenden Druckfarbe, die numerische Werte enthalten.
In нижнетреугольной (Abb. 2), Umgekehrt, Elemente, die im unteren Teil der Matrix sind gleich null.
Gang-Matrix
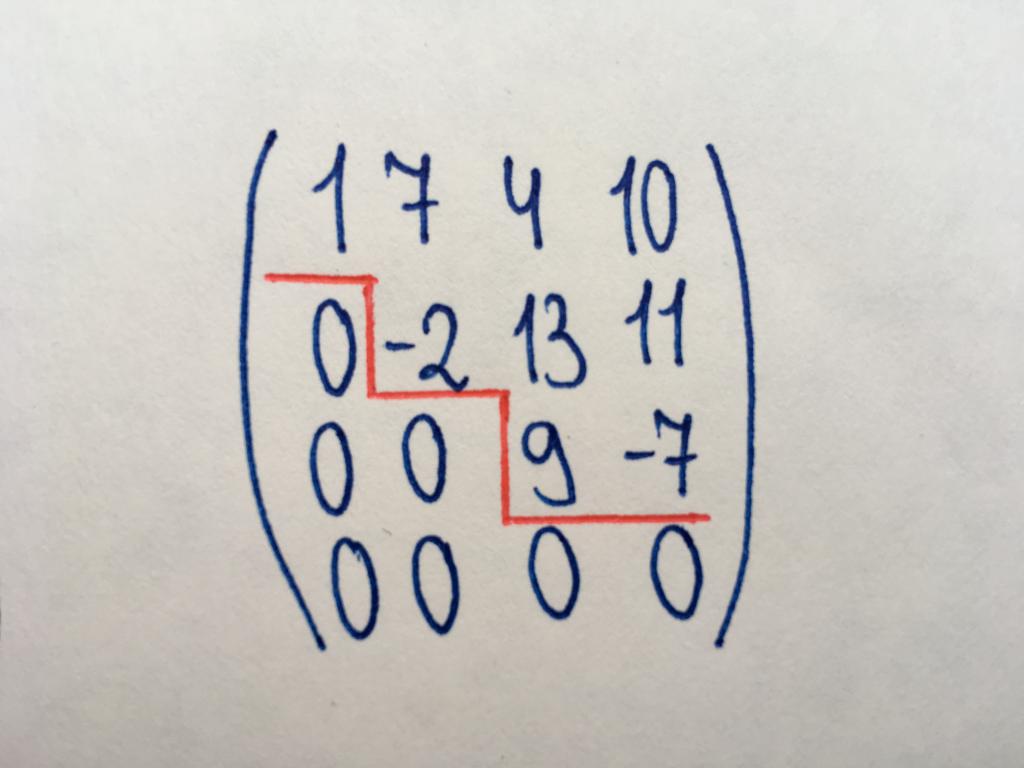
Aussehen ist erforderlich für die Feststellung des Grades der Matrix, sowie für den elementaren Aktionen (zusammen mit Dreieck-Art). Gang-Matrix wird so genannt, weil es enthält die charakteristischen "Stufen" von Nullen (wie abgebildet). In stufenweiser Art bildet die Diagonale aus Nullen (Optional Home), und alle Elemente unter der Diagonale haben auch Werte, die gleich null sind. Voraussetzung ist folgende: wenn in der Stufen-Matrix vorhanden ist, eine null-Zeile, dann die übrigen Zeilen, die sich unterhalb von Ihr, auch nicht numerische Werte enthalten.
So, wir haben die wichtigsten Arten von Matrizen, die für die Arbeit mit Ihnen. Jetzt gehen wir mit der Aufgabe der Umwandlung der Matrix in die gewünschteForm.
Bringing in einer dreieckigen Auge
Wie bringen die Matrix auf der dreieckigen Auge? Meistens in Arbeitsplätze wandeln wir die Matrix in ein dreieckiges Aussehen, um Sie zu finden Determinanten, anders genannt Determinante. Die Durchführung dieses Verfahrens äußerst wichtig "speichern" die Diagonale der Matrix, weil die Determinanten dreieckige Matrix entspricht genau dem Produkt der Komponenten Ihrer Hauptdiagonale. Ich erinnere auch Alternative Methoden finden, die Determinante. Determinanten der quadratischen Typs ist mit speziellen Formeln. Beispielsweise kann mit der Methode des Dreiecks. Für andere Matrizen verwendet die Methode der Zersetzung eine Zeile, eine Spalte oder deren Elemente. Sie können auch die Methode anwenden миноров und algebraischen Erweiterungen der Matrix.
Betrachten wir den Prozess im Detail bringen Sie die Matrix auf der dreieckigen Art von Beispielen auf einige Aufträge.
Aufgabe 1
Sie Müssen eine der vorgestellten Determinanten der Matrix mit der Methode bringen Sie es zu einer dreieckigen Auge.
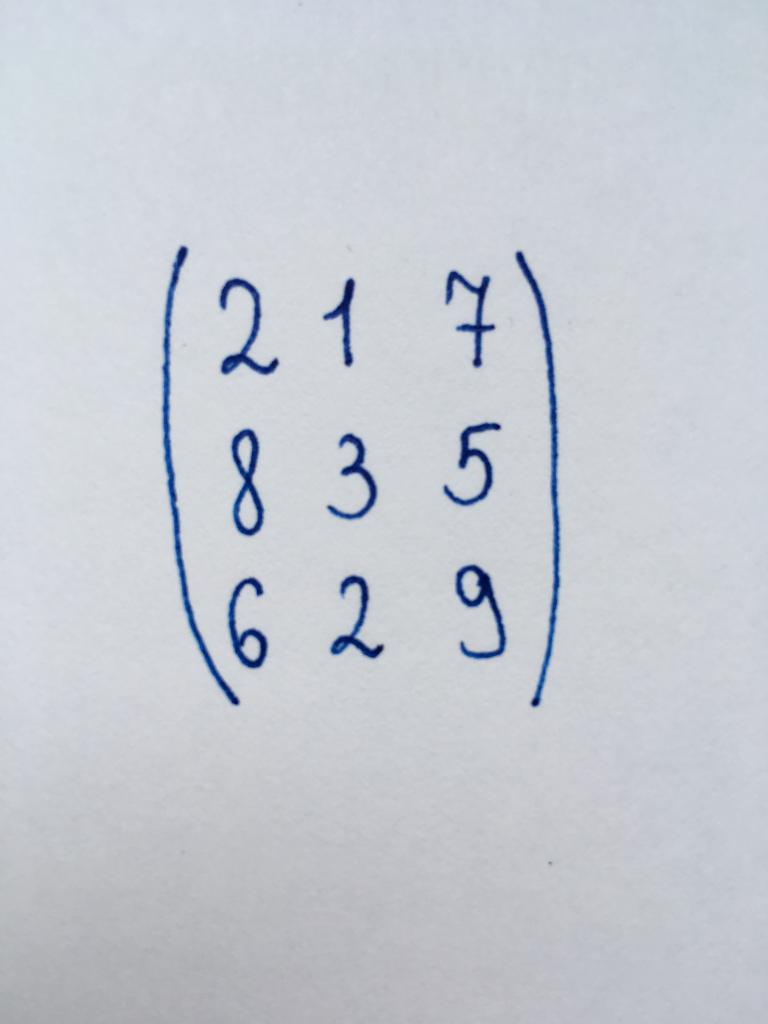
Uns Diese Matrix ist eine quadratische Matrix der Dritten Ordnung. Also, für seine Umwandlung in eine dreieckige Form, müssen wir prüfen auf null zwei Komponenten der ersten Spalte und einer zweiten Komponente.
Damit Sie mit der dreieckigen Auge, beginnen Sie die Umwandlung mit der linken unteren Ecke der Matrix mit der Zahl 6. Um zu versuchen, ihn in der null, multiplizieren Sie die erste Zeile auf drei und subtrahieren Sie von der letzten Zeile.
Wichtig! Die Obere Zeile ändert sich nicht und bleibt die gleiche wie in der ursprünglichen Matrix. Aufzeichnen Zeile, viermal größere ursprünglichen, nicht notwendig. Aber die Werte der Zeilen, die Komponenten müssen auf null, ändern sich ständig.
Als Nächstes machen wir den Wert - Element in der zweiten Zeile der ersten Spalte mit der Zahl 8. Wir multiplizieren die erste Zeile vier und subtrahieren Sie von der zweiten Zeile. Erhalten wir null.
Es Bleibt nur der Letzte Wert - Element der Dritten Zeile der zweiten Spalte. Diese Zahl (-1). Um zu versuchen, ihn im null, in der ersten Zeile subtrahieren wir die zweite.
Führen wir einen Test durch:
DetA = 2 x (-1) x 11 = -22.
Also, die Antwort auf die Aufgabe: -22.
Aufgabe 2
Zu finden Determinanten der Matrix Methode, um es an der dreieckigen Auge.
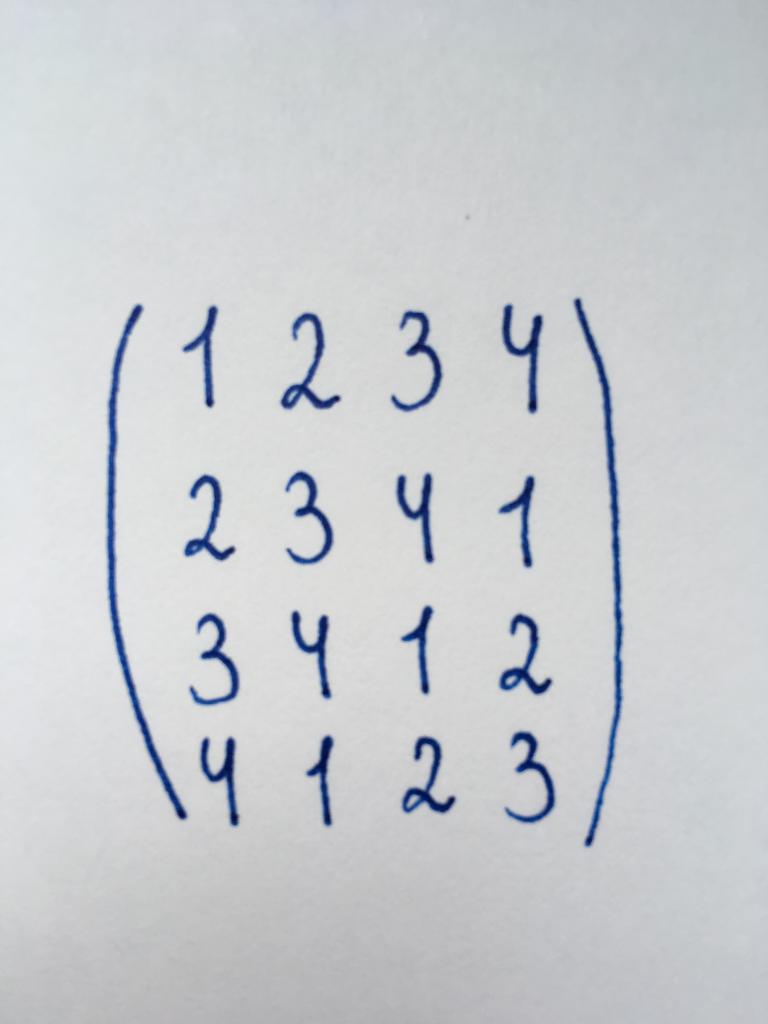
Die Matrix gehört zu den quadratischen Typ und ist die Matrix der vierten Ordnung. Also muss man in null drei Komponenten der ersten Spalte, zwei Komponenten der zweiten Spalte und einer Dritten Komponente.
Fangen wir bringen Sie mit dem Element, das sich in der linken unteren Ecke, mit der Zahl 4. Wir müssen lenken diese Zahl auf null. Am besten, dies zu tun, multiplizieren mit vier oberste Zeile, und dann subtrahieren Sie von der vierten. Schreiben wir das Ergebnis der ersten Bearbeitungsstufe.
Also, die Komponente der vierten Zeile gerichtet auf null. Fahren Sie zum ersten Element der Dritten Zeile, unter 3. Wir führen eine ähnliche Operation. Multipliziert mit drei die erste Zeile, subtrahieren Sie von der Dritten Zeile und schreiben Sie das Ergebnis.
Weiter sehen wir die Zahl 2 in der zweiten Zeile. Wiederholen Sie den Vorgang: multiplizieren wir die Obere Zeile auf zwei und subtrahieren Sie von der zweiten.
Wir es geschafft, die Aufmerksamkeit auf null, alle Komponenten der ersten Spalte einer quadratischen Matrix, mit Ausnahme der Zahl 1 - Element der Hauptdiagonale, ohne Konvertierung. Jetzt ist es wichtig, die Nullen, so werden die Durchführung der Umwandlung mit Strings, aber nicht mit Spalten. Gehen Sie auf die zweite Spalte der vorgestellten Matrix.
Wieder beginnen mit dem unteren Teil - mit dem Element in der zweiten Spalte der letzten Zeile. Diese Zahl (-7). In diesem Fall ist jedoch bequemer, beginnen mit einer Zahl (-1) - Element der zweiten Spalte der Dritten Zeile. Um zu versuchen, ihn auf null, subtrahieren der Dritten Zeile die zweite. Dann multiplizieren Sie die zweite Zeile sieben und ziehen Sie aus dem vierten. Wir haben null anstelle des Elements befindet sich in der vierten Zeile der zweiten Spalte. Wir kommen nun zur Dritten Spalte.
In dieser Spalte müssen wir umkehren auf null nur eine Zahl - 4. Machen Sie es einfach: einfach addieren zu der letzten Zeile der Dritten und sehen uns die gewünschte null.
Nach allen gemachten Transformationen führten wir die vorgeschlagene Matrix zu dreieckigen Augen. Nun, um Sie zu finden Determinanten, müssen nur produzieren, resultierenden Multiplikation der Elemente der Hauptdiagonale. Wir erhalten: DetA = 1 x (-1) x (-4) x 40 = 160. Also, die Lösung ist die Anzahl von 160.
Also jetzt die Frage bringen die Matrix auf der dreieckigen Art von Sie bitte.
Bringing stufigen Verstärkungseinstellung zu beachten
Bei elementaren Operationen auf Matrizen Stufen-look ist weniger "gefragt" als dreieckig. Es wird am häufigsten für die Feststellung des Grades der Matrix (d.h. die Anzahl der Zeilen ungleich null) oder zur Bestimmung der Linear abhängigen und unabhängigen Zeilen. Jedoch stufige Matrix-Ansicht ist vielseitiger, da eignet sich nicht nur für quadratische Art, sondern auch für alle anderen.
Um die Matrix führen stufigen Verstärkungseinstellung zu den Augen, zuerst müssen Sie Ihre Determinanten. Dazu passen die oben genannten Methoden. Ziel des Verbleibs Determinante ist: herauszufinden, ob die Umwandlung Stufen-Matrix-Ansicht. Wenn Determinanten größer oder kleiner als null ist, dann kann man sicher damit beginnen, sich auf die Aufgabe. Wenn er gleich null ist, Sie eine Umwandlung vornehmen Matrix zur stufigen Verstärkungseinstellung Augen nicht funktionieren. In diesem Fall sollten Sie überprüfen, ob es keine Fehler in der Aufnahme oder in Matrix-Transformationen. Wenn solche Ungenauigkeiten nicht, die Aufgabenicht gelöst werden kann.
Betrachten Sie, wie bringen Sie die Matrix zur stufigen Verstärkungseinstellung Art von Beispielen mehrerer Aufträge.
Aufgabe 1. Suchen Grad der Matrix-Tabelle.
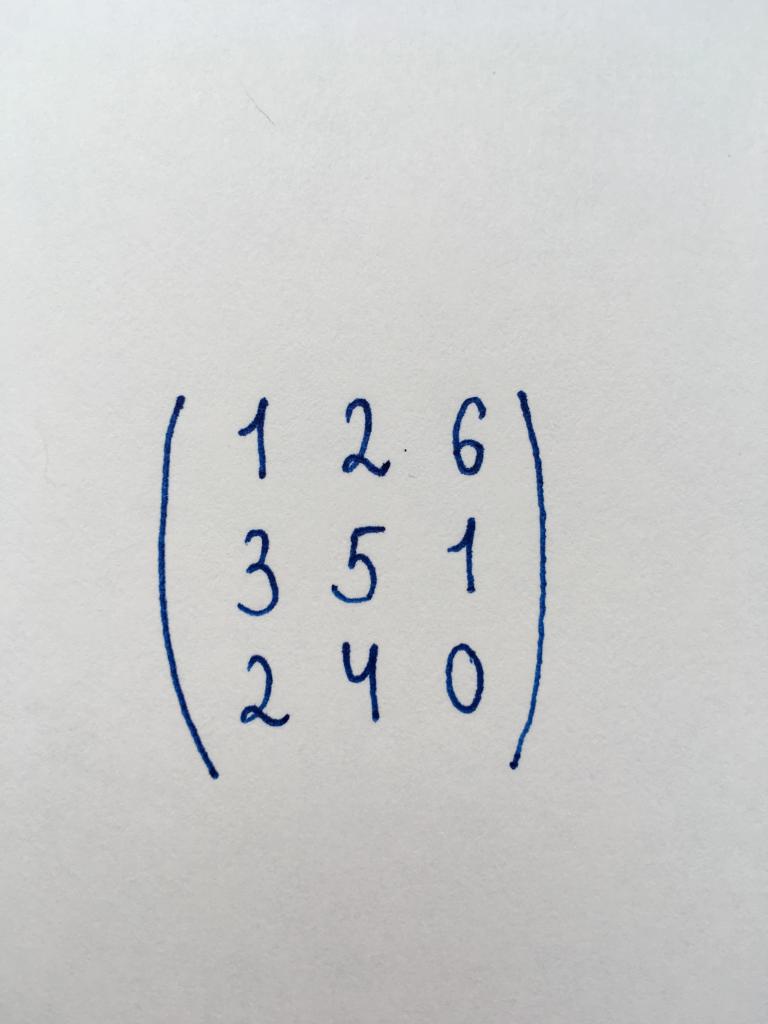
Vor uns die quadratische Matrix Dritter Ordnung (3x3). Wir wissen, dass für die Feststellung des Grades erforderlich führen stufigen Verstärkungseinstellung Auge. Also zuerst müssen wir die Determinante der Matrix. Wir verwenden die Methode des Dreiecks: DetA = (1 5 x-x 0) + (2 x 1 x 2) + (6 x 3 x 4) - (1 x 1 x 4) - (2 x-3 x-0) - (6 x 5 x 2) = 12.
Determinanten = 12. Er ist größer als null, bedeutet das, dass eine Matrix kann dazu führen stufigen Verstärkungseinstellung Auge. Fangen wir mit Ihrer Transformationen.
Beginnen wir es mit einem Element der linken Spalte der Dritten Zeile - Zahl 2. Multiplizieren wir die Obere Zeile auf zwei und subtrahieren Sie von der Dritten. Dank dieser Operation wie das von uns gewünschte Element, und die Zahl der 4 - Element der zweiten Spalte der Dritten Zeile - gerichtet auf null.
Weiter lenken auf null ist ein Element der zweiten Zeile der ersten Spalte - Zahl 3. Dafür multiplizieren wir die Obere Zeile drei und subtrahieren Sie von der zweiten.
Wir sehen, dass infolge der Verminderung entstand die dreieckige Matrix. In unserem Fall wird die Konvertierung fortgesetzt werden darf, da die anderen Komponenten nicht in der Lage, die Aufmerksamkeit auf null.
Also folgern, dass die Anzahl der Zeichenfolgen mit numerischen Werten in der Matrix (oder deren Qualität) - 3. Die Antwort auf die Aufgabe: 3.
Aufgabe 2. Bestimmen Sie die Anzahl der Linear unabhängigen Zeilen der Matrix.
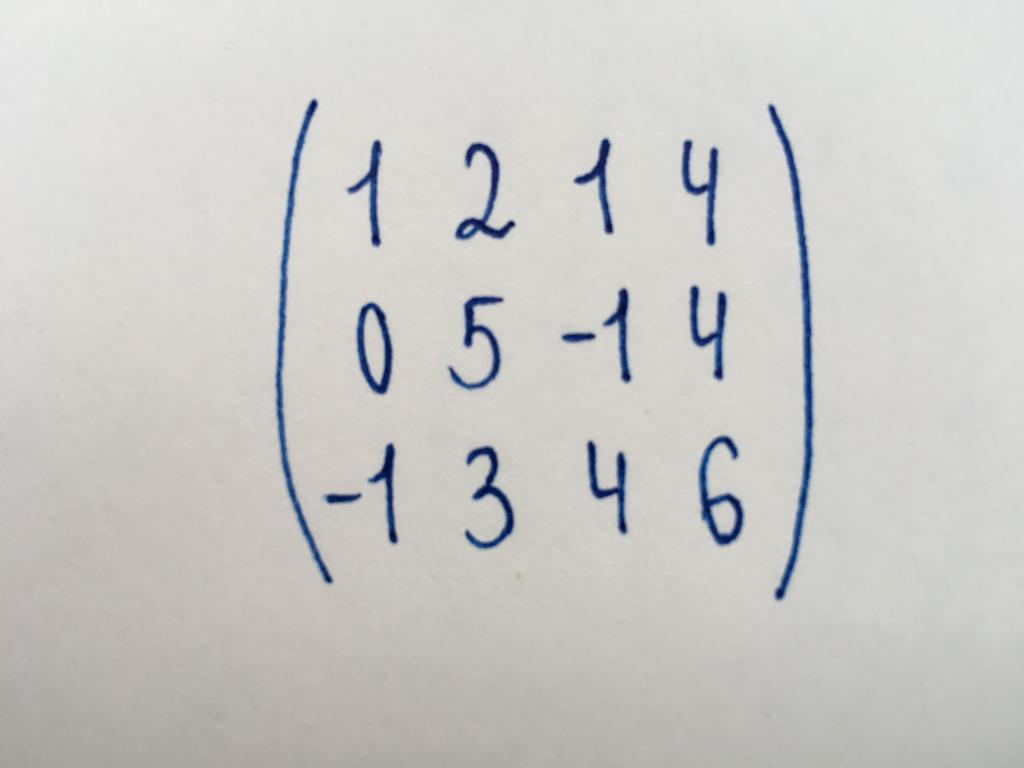
Wir brauchen eine solche Zeichenfolgen, die nicht mit irgendwelchen Transformationen auf null ziehen. In der Tat müssen wir eine Anzahl Zeilen ungleich null, oder der Grad der vorgestellten Matrix. Dazu machen Sie eine Vereinfachung.
Wir sehen die Matrix, nicht im Besitz von dem quadratischen Typ. Es hat eine Größe von 3x4. Wir beginnen auch mit Anführung der linken unteren Ecke des Elements - Zahl (-1).
Addieren die erste Zeile zur Dritten. Weiter ziehen daraus die zweite, aufzuheben, die Zahl 5 auf null.
Ihre Weitere Umwandlung ist nicht möglich. Also, schließen wir, dass die Anzahl der Linear unabhängigen Zeilen in Ihr und die Antwort auf die Aufgabe - 3.
Jetzt Matrix auf die Anführung stufigen Verstärkungseinstellung Art von ist nicht für Sie undurchführbar Aufgabe.
Für Beispieldaten Aufgaben besprachen wir die Anführung der Matrix zu dreieckigen Augen und stufigen Verstärkungseinstellung Auge. Damit zeichnen die Werte auf null Matrix-Tabellen, in einigen Fällen ist es erforderlich, Ideen zu entwickeln und richtig zu konvertieren, Spalten oder Zeilen. Ich Wünsche Ihnen viel Erfolg in der Mathematik und in der Arbeit mit Matrizen!
Article in other languages:

Alin Trodden - autor des Artikels, Herausgeber
"Hi, ich bin Alin Trodden. Ich schreibe Texte, lese Bücher und suche nach Eindrücken. Und ich bin nicht schlecht darin, dir davon zu erzählen. Ich freue mich immer, an interessanten Projekten teilzunehmen."
Verwandte News
Telegramm... Dieses Wort kann zaubern vergilbten Bild ramponierte Stück Papier, enthaltend eine Nachricht über den Fernen historischen Ereignissen, wenig im Zusammenhang mit der modernen Welt. Doch viele Möglichkeiten, die wir jet...
Die großen geographischen Entdeckungen
15-17 Jahrhunderte haben bedeutende Spur in der Geschichte und Wirtschaft der ganzen Menschheit. In dieser Zeit treten die Großen geographischen Entdeckungen, die Voraussetzung für die Entwicklung der bürgerlichen Produktionsweise...
Aufsatz zum Thema "Heimat" - wie Schreibe ich eine patriotische Geschichte?
darüber, wie Schreibe ich einen Aufsatz zum Thema "Heimat", sagen die Pädagogen, bevor Sie geben den Schülern diese Aufgabe. Und im Allgemeinen ist alles klar, aber was sollte Stilistik, und was konkret zu erzählen? Sollte alles z...
Die japanischen Städte: ob Sie besuchen das Land der aufgehenden Sonne?
Bei den meisten Slawen es wird angenommen, dass die Kultur Japans – „Sushi, Hieroglyphen und Kimono». Enge Vorstellung von einer der am höchsten entwickelten Länder der Welt verbunden mit dem niedrigen Niveau der...
Lado Кецховели: Leben und Tod des Revolutionärs
lado Кецховели war einer der wichtigsten Mitglieder der SDAPR in Transkaukasien. Er beschäftigte sich mit der gewerblichen Tätigkeit und Propaganda unter den Arbeitern. Mit ihm in seiner Jugend arbeitete Joseph Stalin. Кецховели s...
Eurasia - das Festland spült Ozean 4
Diese Frage kann fallen in Tests in der Geographie oder in einem Kreuzworträtsel: Festland, die wäscht 4 Ozeans? Ein gebildeter Mensch weiß genau die richtige Antwort. Nun, wenn Sie noch nicht kennt, dann wird es gemeinsam mit uns...






















Kommentare (0)
Dieser Artikel wurde noch kein Kommentar abgegeben, sei der erste!