أنواع المصفوفات. خطوة مصفوفة. وبذلك المصفوفة إلى الخطوة الثلاثي شكل
المصفوفة هو كائن خاص في الرياضيات. يصور في شكل طاولة مربعة أو مستطيلة ، التي تتألف من عدد من الصفوف والأعمدة. في الرياضيات هناك مجموعة كبيرة ومتنوعة من المصفوفات التي تختلف في الحجم أو المحتوى. عدد الصفوف والأعمدة يشار إلى أوامر. هذه الكائنات تستخدم في الرياضيات تنظيم السجل الخاص بك نظم المعادلات الخطية و سهل نتائج البحث. المعادلات باستخدام مصفوفة يتم حلها من خلال طريقة كارل غاوس ، غابرييل كريمر والقصر جبري الإضافات, فضلا عن العديد من الطرق الأخرى. المهارات الأساسية في العمل مع المصفوفات هو جلب إلى طريقة العرض القياسية. ولكن أولا دعونا نرى ما هو نوع من مصفوفة معزولة الرياضيات.
Null نوع
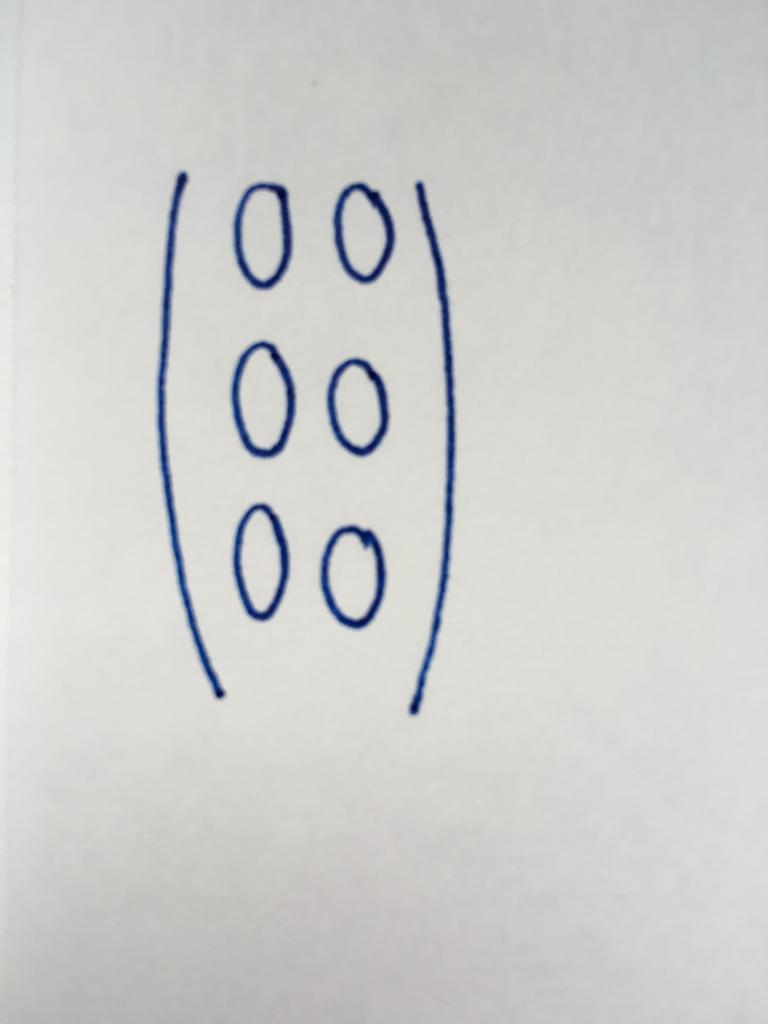
جميع عناصر هذه المصفوفة هي صفر. وفي الوقت نفسه ، فإن عدد الصفوف والأعمدة هي مختلفة تماما.
نوع مربع
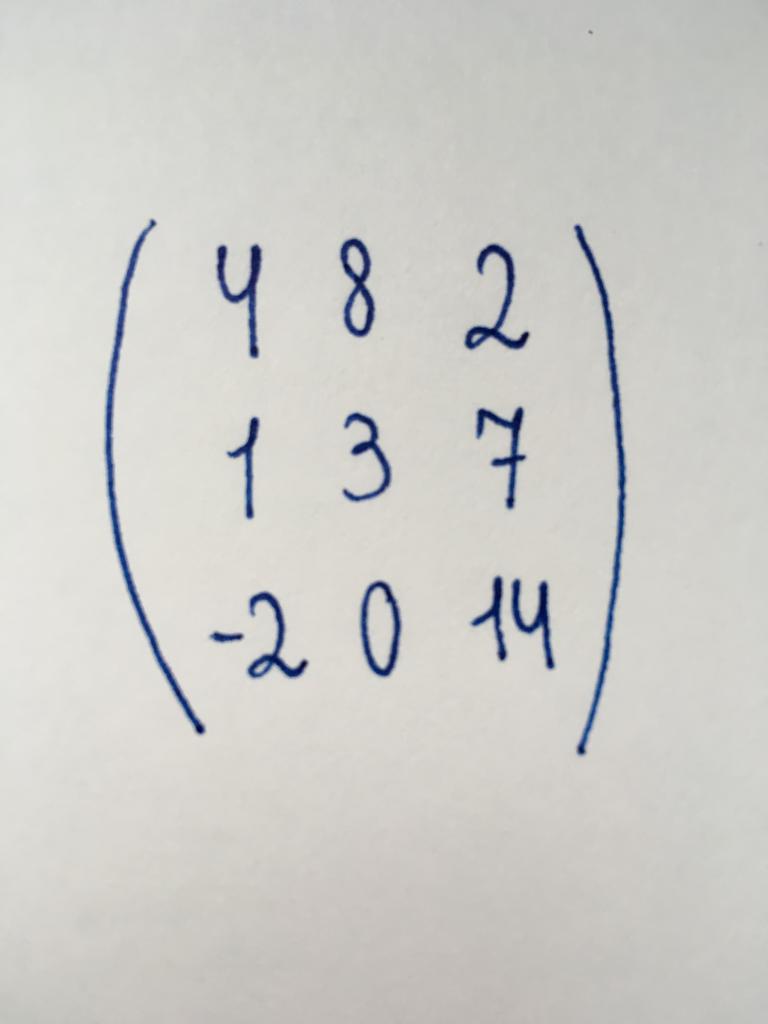
عدد الأعمدة والصفوف من هذه المصفوفة هو نفسه. وبعبارة أخرى ، هو جدول شكل "مربع". عدد الأعمدة (أو الصفوف) وتسمى النظام. خاصة الحالات التي تعتبر وجود مصفوفة من الدرجة الثانية (مصفوفة 2 × 2), الرابع (4x4) عشرة (10x10) والسابع (17x17), وهلم جرا.
ناقلات Stober
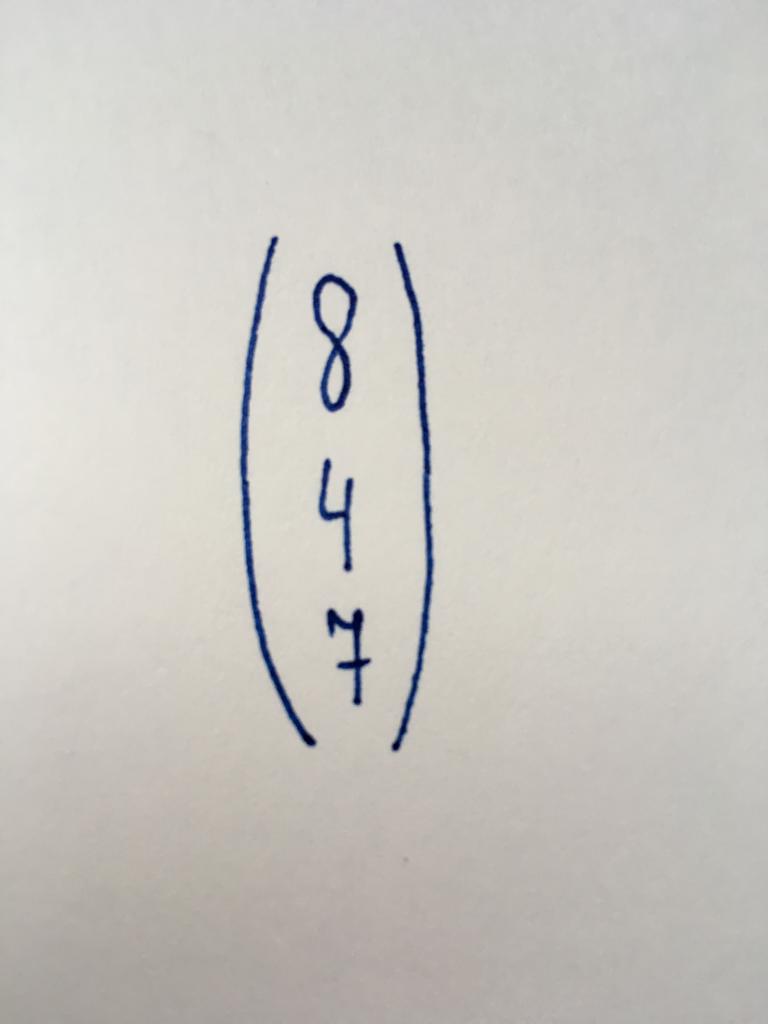
هذا هو واحد من أبسط أنواع من المصفوفة التي تحتوي على عمود واحد فقط ، والذي يتألف من ثلاثة القيم الرقمية. أنه يمثل عدد من أعضاء (الأرقام التي هي المتغيرات المستقلة) أنظمة المعادلات الخطية.
ناقل خط
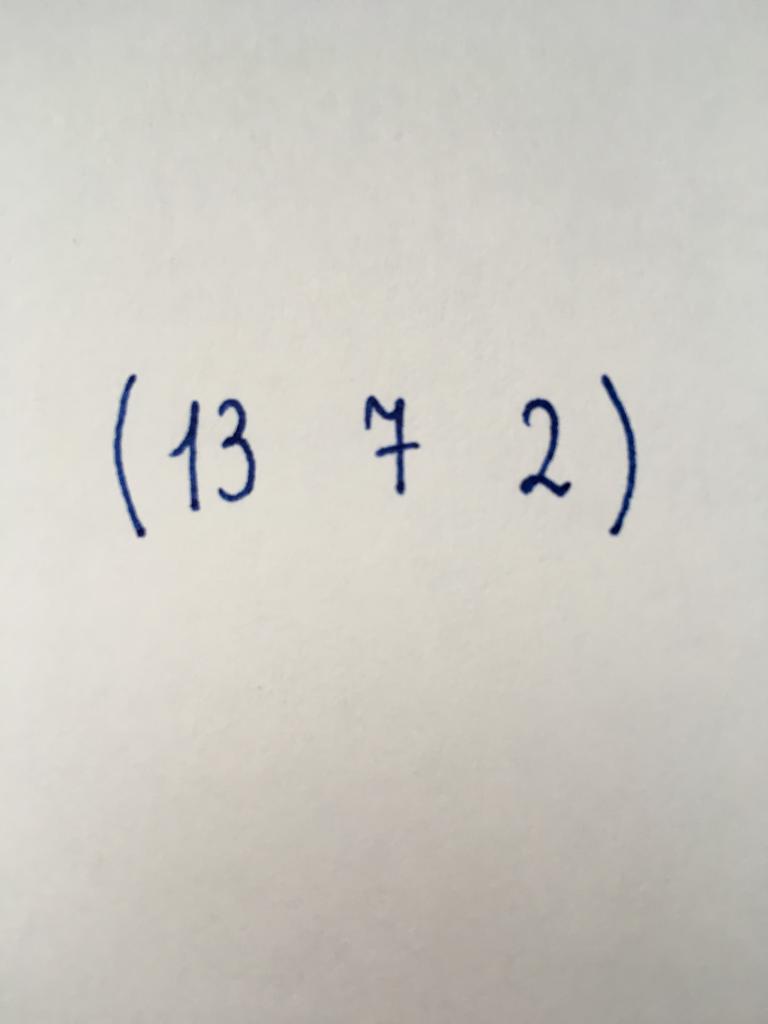
مماثلة في السابق. يتكون من ثلاثة العددية العناصر بدورها مرتبة في صف واحد.
قطري
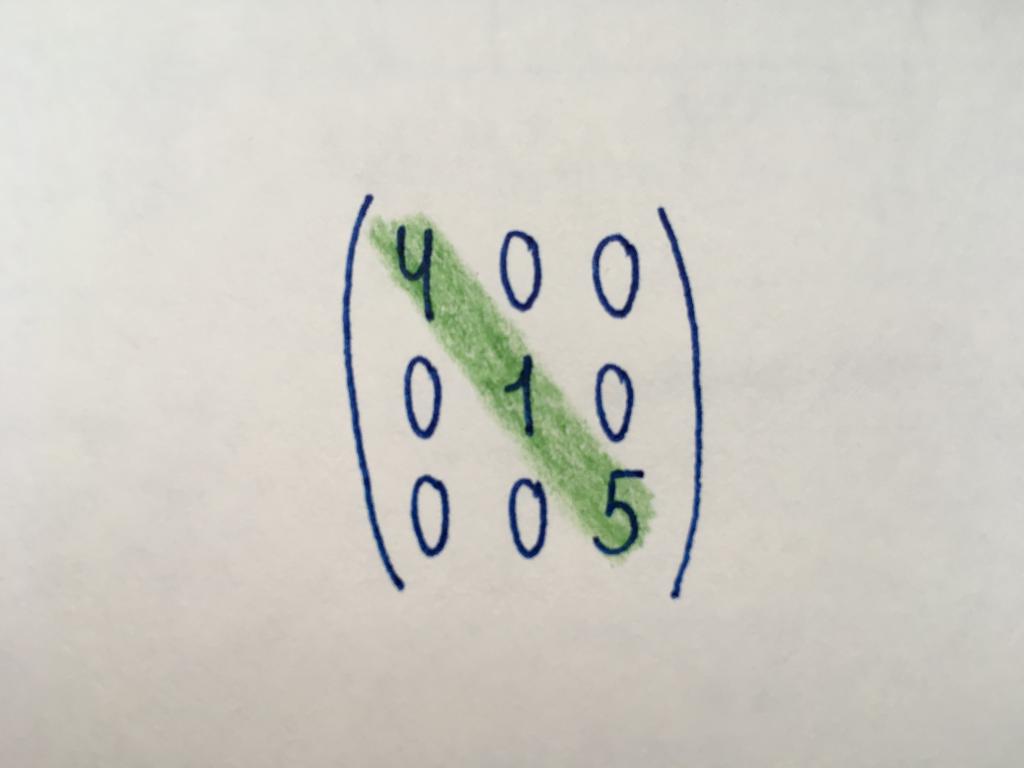
القيم الرقمية في مصفوفة قطرية أخذ المكونات الرئيسية قطري (باللون الأخضر). الرئيسية قطري يبدأ مع عنصر في الركن العلوي الأيمن وتنتهي في العمود الثالث من الصف الثالث. المكونات المتبقية تساوي الصفر. قطري نوع فقط يمثل مصفوفة مربعة من أي أمر. بين قطري المصفوفات ، هناك العددية. جميع مكونات تأخذ نفس القيمة.
المزيد
أساليب التدريس التفاعلية في جامعة
أساليب التدريس التفاعلية هي واحدة من أهم وسائل تحسين التدريب المهني من الطلاب في التعليم العالي. المعلم هو الآن لا يكفي أن تكون ببساطة المختصة في الانضباط ، وإعطاء المعرفة النظرية في الفصول الدراسية. تحتاج بعض نهج مختلف الحديثة في العملية التعليمية.ن...
البرازيل الذي أعداد السكان في المرتبة الخامسة المرتبة الثانية بعد الهند والصين وإندونيسيا وأمريكا – متنوعة جدا البلد. لعدة مئات من السنين الأمة أصبح من أهم العرقية-الثقافية والتعليم. سكان البرازيل هو أكثر من مائة القوميات والشعوب. في هذا ...
مستعمرة من بريطانيا – العديد من المناطق في جميع أنحاء العالم ، الذين تم القبض عليهم ، تؤخذ تحت الحماية أو بعض الوسائل المكتسبة بين 16 و 18 قرون واحدة من أقوى الإمبراطوريات في الماضي – البريطانية. وكان الهدف من التنمية الإقليمية. خلال الفت...
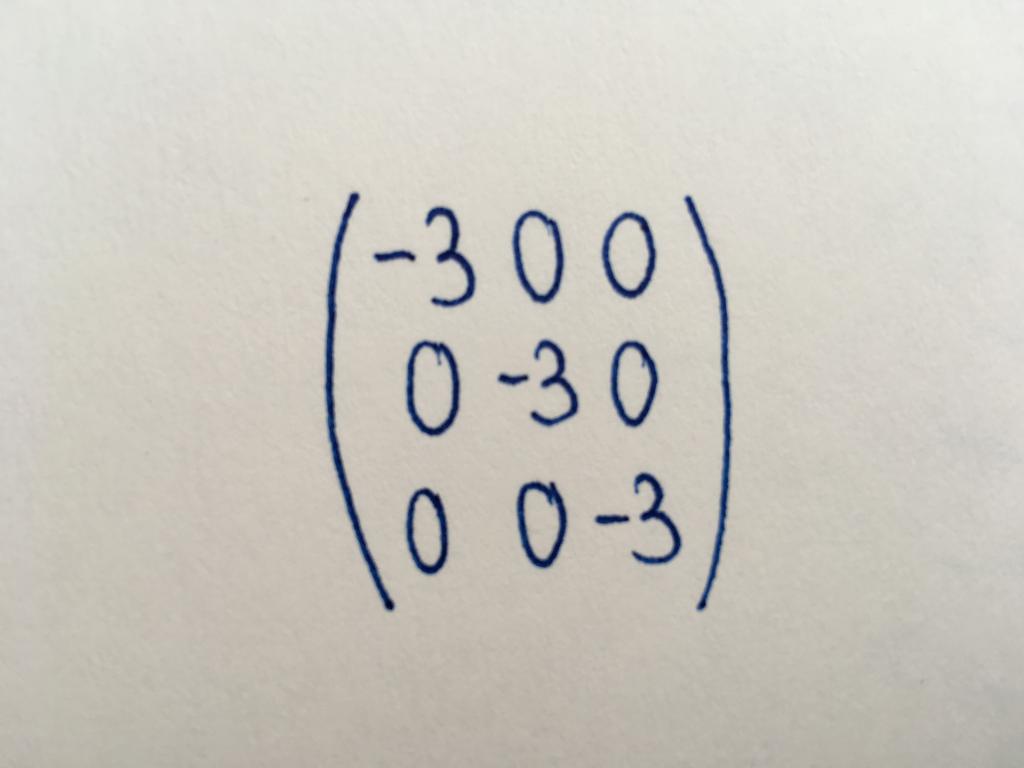
الهوية مصفوفة
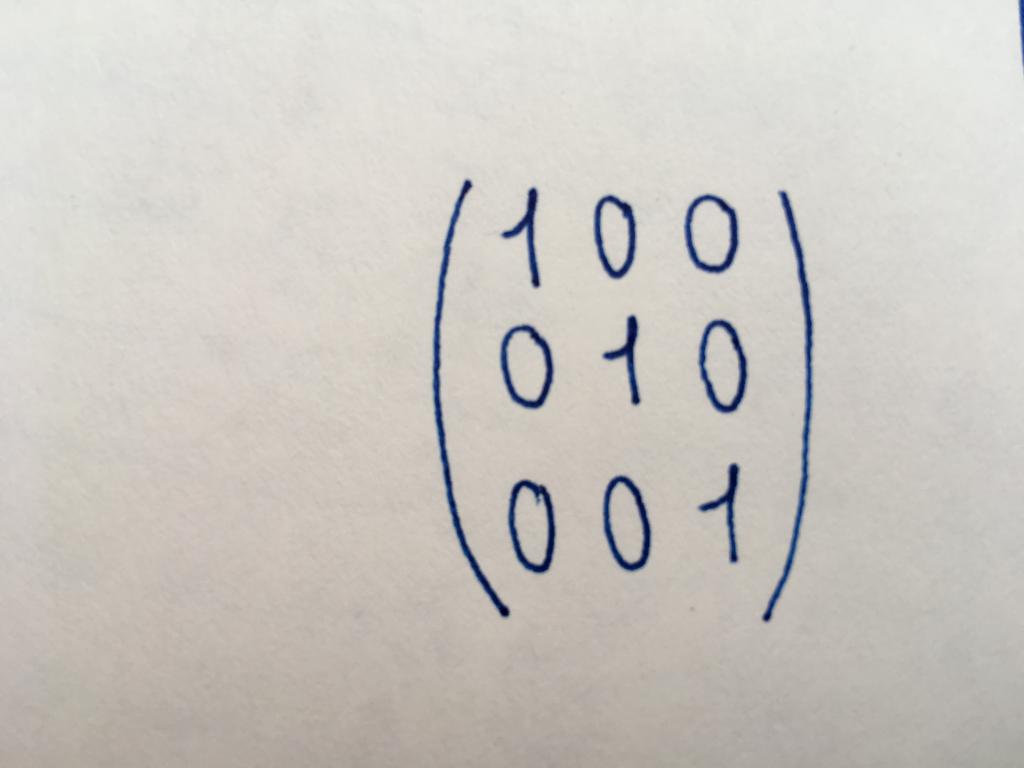
نوع من أنواع قطري من المصفوفة. كل القيم العددية الوحدات. باستخدام نوع واحد من مصفوفة جداول تنفيذ قاعدة التحويلات أو إيجاد معكوس من المصدر.
الكنسي نوع
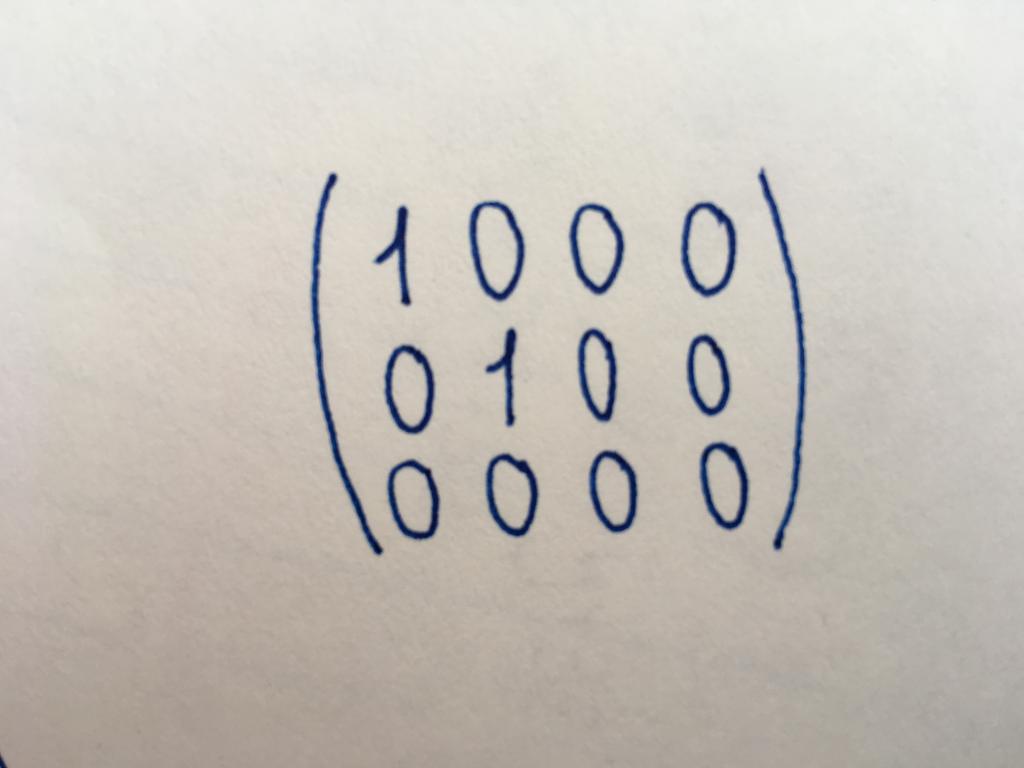
الكنسي شكل المصفوفة هو واحد من أهم و التعديل الضروري في كثير من الأحيان. عدد الصفوف والأعمدة في الكنسي مصفوفة مختلفة ، وأنها لا تنتمي بالضرورة إلى نوع مربع. وهي تشبه إلى حد ما مصفوفة الهوية ، ولكن في حال ليس كل المكونات الرئيسية قطري يتم تعيين يساوي واحد. Pavlovianly الوحدات قد يكون اثنين أو أربعة (اعتمادا على طول وعرض المصفوفة). أو الوحدات قد لا تكون متاحة في جميع (عندما يكون الصفر). المكونات المتبقية الكنسي نوع عناصر قطري واحد صفر.
الثلاثي
واحدة من أهم أنواع مصفوفة المستخدمة في البحث عن العوامل التي في أداء العمليات البسيطة. الثلاثي نوع مشتق من قطري ، حتى المصفوفة هو أيضا مربع. الثلاثي شكل مصفوفة مقسمة إلى vernetroyerinpy و negativly.

في vernerable مصفوفة (Fig. 1) العناصر التي هي فوق الرئيسية قطري يتم تعيين إلى الصفر. مكونات قطري المصفوفة مرتبة أقل من ذلك ، تحتوي على قيم عددية.
في Nizhneserginsky (Fig. 2) على العكس من ذلك ، فإن العناصر الموجودة في الجزء السفلي من المصفوفة يساوي صفر.
الخطوة مصفوفة
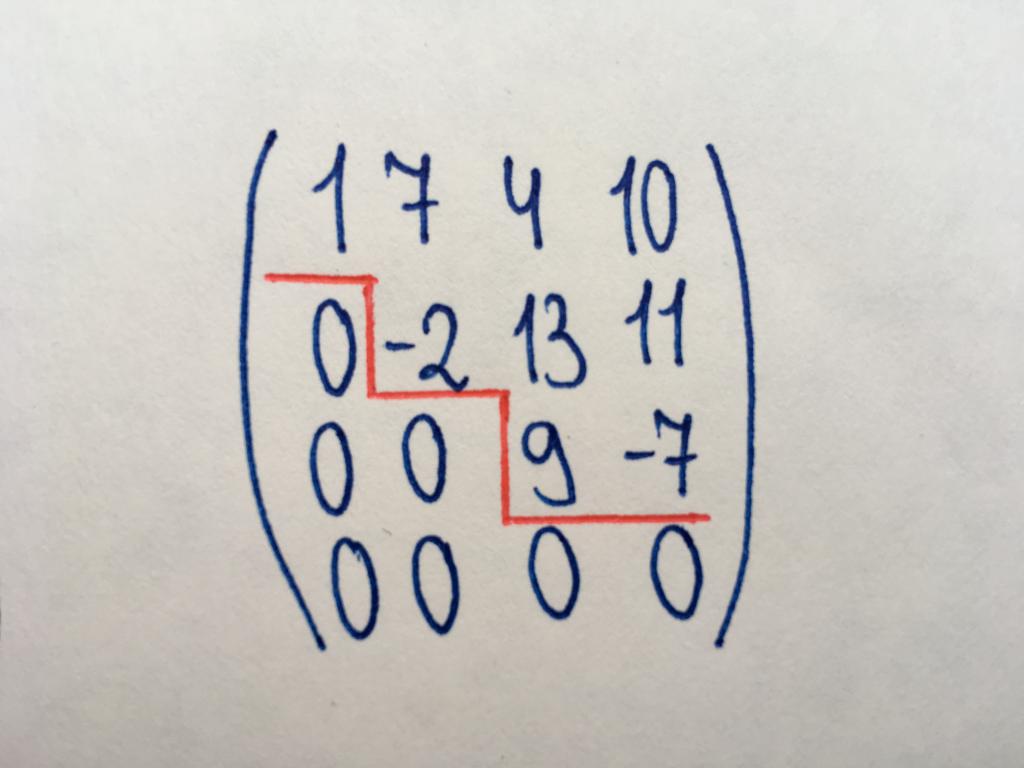
مطلوب للعثور على رتبة المصفوفة الابتدائية العمليات عليها (جنبا إلى جنب مع نوع الثلاثي). الخطوة المصفوفة سميت بذلك لأنه يحتوي على سمة "خطوات" من الأصفار (كما هو مبين في الشكل). في صعدت نوع أشكال قطري من الأصفار (ليس بالضرورة المهم) ، وجميع العناصر أدناه قطري القيمة صفر. إلزامية الشرط التالي: إذا كانت الخطوة مصفوفة هناك null-سلسلة, سلاسل أخرى أقل من ذلك ، كما لا تحتوي على قيم عددية.
وهكذا ، فإننا تعتبر أهم أنواع المصفوفات في حاجة إلى العمل معهم. الآن دعونا التعامل مع مهمة تحويل المصفوفة إلى المطلوبشكل.
تخفيض النموذج الثلاثي
كيفية تحويل المصفوفة إلى مثلثة الشكل ؟ في معظم الأحيان المهام اللازمة لتحويل المصفوفة على شكل الثلاثي ، للعثور على محدداتها وإلا دعا المحدد. تنفيذ هذا الإجراء ، من المهم أن "حفظ" قطري الرئيسي من المصفوفة لأن محددا من الثلاثي مصفوفة يساوي المنتج من مكونات الرئيسية قطري. اسمحوا لي أن أذكركم أيضا طرق بديلة وإيجاد المحدد. المحدد من مربع مع المعونة من الصيغ الخاصة. على سبيل المثال ، يمكنك استخدام طريقة المثلث. الأخرى المصفوفات باستخدام أسلوب التحلل من الصف أو العمود أو العناصر. ومن الممكن أيضا تطبيق طريقة القصر جبري الإضافات من المصفوفة.
تحليل بالتفصيل عملية إدخال مصفوفة على شكل الثلاثي على أمثلة من بعض الوظائف.
مهمة 1
تحتاج إلى العثور على محدد المصفوفة ، وذلك باستخدام طريقة ليصل إلى الشكل الثلاثي.
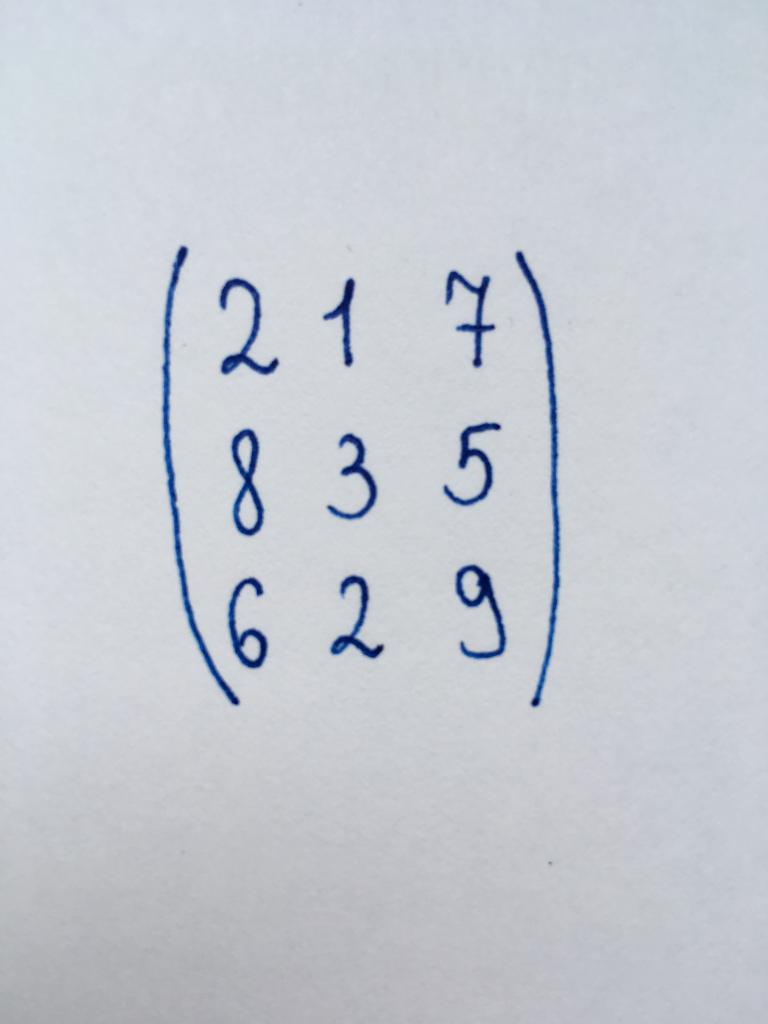
أعطانا مصفوفة مصفوفة مربعة من المرتبة الثالثة. وبالتالي تحويلها إلى شكل الثلاثي ، نحن بحاجة إلى اللجوء إلى الصفر عنصرين من أول عمود واحد العنصر الثاني.
أن نصل إلى شكل الثلاثي ، نبدأ في التحول من الزاوية اليسرى السفلى من المصفوفة مع عدد 6. لتحويله إلى الصفر ، نضرب الصف الأول قبل ثلاثة طرح من الصف الأخير.
المهم! الصف العلوي هو لا يتغير و لا يزال هو نفسه كما في النص الأصلي مصفوفة. لكتابة سلسلة أربع مرات مصدر كبير ليس من الضروري. ولكن سلسلة القيم المكونات التي تحتاج إلى دفع في صفر المتغيرة باستمرار.
دعونا مزيد من القيمة التالية عناصر من الصف الثاني من العمود الأول ، 8 في العدد. ضرب الصف الأول قبل أربعة وطرح من الصف الثاني. سوف تتلقى صفر.
ولم يتبق سوى القيمة الأخيرة هي عنصر من الصف الثالث من العمود الثاني. هذا العدد (-1). أن تتحول إلى صفر أول من طرح الصف الثاني.
أداء الاختبار:
ديتا = 2 × (-1) × 11 = -22.
الجواب الوظيفة: -22.
التمرين 2
تحتاج إلى العثور على محدد مصفوفة من قبل ليصل إلى الشكل الثلاثي.
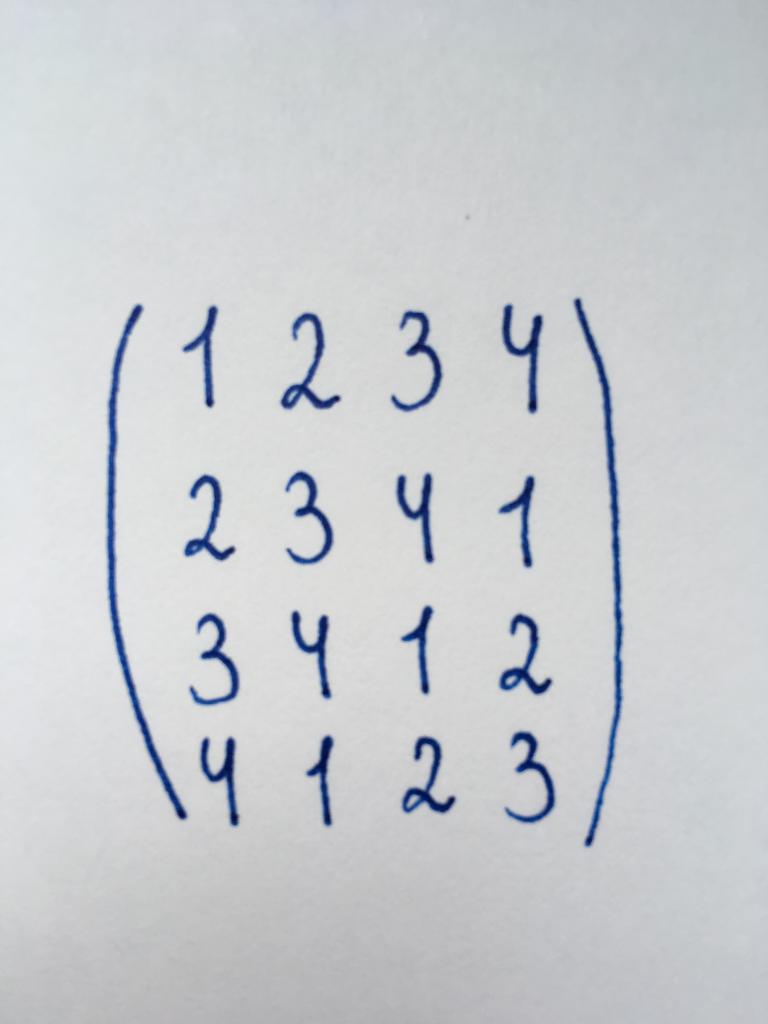
المصفوفة ينتمي إلى نوع مربع و هو مصفوفة من المرتبة الرابعة. لذا عليك أن تدفع في صفر ثلاثة من عناصر العمود الأول ، عنصرين من العمود الثاني واحدة من العنصر الثالث.
دعونا نبدأ تحقيق مع عنصر في الزاوية اليسرى السفلى مع عدد 4. نحن بحاجة إلى عكس هذا الرقم إلى الصفر. الأكثر ملاءمة للقيام بذلك بضرب رأس أربعة السلسلة ، ومن ثم طرح ذلك من الرابعة. كتابة نتيجة المرحلة الأولى من عملية التحويل.
لذلك المكون من السطر الرابع تحويلها إلى صفر. الانتقال إلى العنصر الأول في السطر الثالث ، العدد 3. تنفيذ نفس العملية. ضرب من قبل ثلاثة الصف الأول ، طرح من الصف الثالث وسجل النتيجة.
التالي نرى عدد 2 في السطر الثاني. كرر العملية: ضرب الصف العلوي من قبل اثنين من طرح ذلك من الثاني.
كنا قادرين على الدفع إلى الصفر كل مكونات العمود الأول من هذا مصفوفة مربعة ، باستثناء عدد 1 - العناصر الرئيسية قطري التي لا تتطلب التحويل. من المهم الآن الحفاظ على الأصفار ، لذا سيتم تحويل إلى الصفوف لا الأعمدة. انتقل إلى العمود الثاني يمثل مصفوفة.
مرة أخرى ، تبدأ مع الجزء السفلي - مع عناصر العمود الثاني من الصف الأخير. هذا الرقم (-7). ومع ذلك ، في هذه الحالة هو أكثر ملاءمة أن تبدأ مع عدد (-1) - عناصر العمود الثاني من الصف الثالث. لتحويله إلى الصفر ، طرح من الصف الثالث إلى الثاني. ثم ضرب الثانية على التوالي من قبل سبعة وطرح من الرابعة. لدينا الصفر بدلا من عنصر يقع في الصف الرابع من العمود الثاني. ننتقل الآن إلى العمود الثالث.
في هذا العمود ، نحن بحاجة إلى إيلاء الصفر رقم واحد فقط - 4. فمن السهل القيام به: فقط إضافة إلى السطر الأخير من الثالثة ونحن نرى أننا في حاجة إلى الصفر.
بعد كل التحولات لقد جلبت المصفوفة المقترحة على الشكل الثلاثي. الآن ومحدداتها ، فمن الضروري فقط لأداء الضرب الناتجة العناصر الرئيسية قطري. الواردة: ديتا = 1 × (-1) × (-4) × 40 = 160. وبالتالي فإن الحل هو الرقم 160.
حتى الآن في مسألة تخفيض مصفوفة على شكل الثلاثي فضلك.
جلب إلى الأذهان الخطوة
مع أبسط العمليات على المصفوفات صعدت مظهر أقل "شعبية" من الثلاثي. هو الأكثر شيوعا للعثور على رتبة المصفوفة (أي عدد غير صفرية الصفوف) أو تعريف الخطية مستقل الصفوف. ومع ذلك ، فإن صعدت شكل المصفوفة هو أكثر تنوعا كما هو مناسبة ليس فقط نوع مربع ، ولكن كل الآخرين.
لجلب المصفوفة إلى سرعة العقل, تحتاج أولا إلى العثور على محدداته. لهذا تناسب الأساليب السابقة. الهدف من إيجاد المحددات على النحو التالي: معرفة ما إذا كان يمكنك تحويله إلى الخطوة مصفوفة. إذا كان العامل هو أكبر من أو أقل من الصفر ، ثم يمكنك أن تنتقل بأمان إلى العمل. إذا كان الصفر ، يلقي المصفوفة إلى سرعة العقل لا يعمل. في هذه الحالة, تحتاج إلى التحقق من ما إذا كان هناك أي أخطاء في السجل أو في مصفوفة التحويل. إن هذه المغالطات لا وظيفةفإنه من المستحيل حلها.
النظر في كيفية تحويل المصفوفة إلى سرعة اعتبارها أمثلة متعددة الوظائف.
مهمة 1. للعثور على مرتبة من هذه المصفوفة.
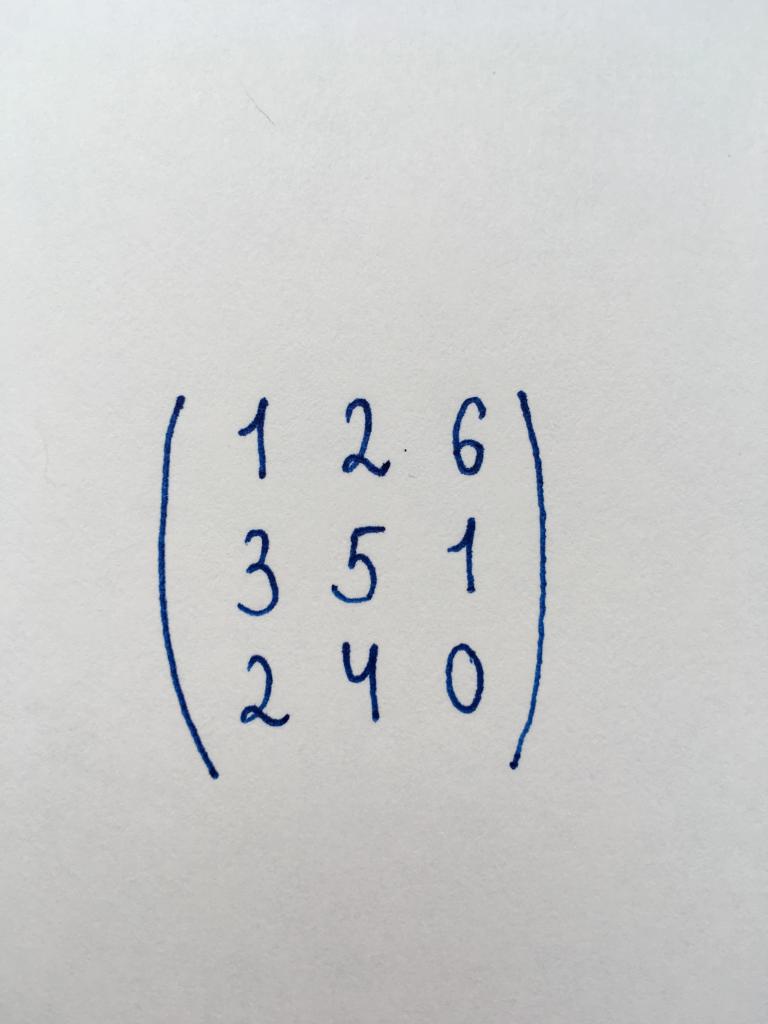
قبل الولايات المتحدة هي مصفوفة مربعة من المرتبة الثالثة (3x3). نحن نعلم أن تجد الصف يجب عليك أن تحضر إلى سرعة العقل. لذلك أولا نحن بحاجة إلى العثور على محدد المصفوفة. نحن نستخدم طريقة المثلث: ديتا = (1 × 5 × 0) + (2 × 1 × 2) + (6 × 3 × 4) - (1 × 1 × 4) - (2 × 3 × 0) - (6 × 5 × 2) = 12.
المحددات = 12. هو أكبر من الصفر, ثم المصفوفة يمكن أن يؤدي إلى سرعة العقل. بداية التحول.
نبدأ مع عنصر في العمود الأيسر من الصف الثالث ، أرقام 2. ضرب الصف العلوي من قبل اثنين وطرح عليه من الثلث. بفضل هذه العملية اللازمة العنصر رقم 4 عناصر العمود الثاني من الصف الثالث تحولت إلى صفر.
ورسم الصفر عنصر من الصف الثاني من العمود الأول هو رقم 3. للقيام بذلك ضرب الصف العلوي قبل ثلاثة طرح من الثانية.
يمكننا أن نرى أن يلقي تشكلت من الثلاثي مصفوفة. في حالة الاستمرار في التحويل من المستحيل ، حيث المكونات الأخرى لن تكون قادرة على دفع إلى الصفر.
لذا ، فإننا نستنتج أن عدد الصفوف التي تحتوي على قيم رقمية في المصفوفة (أو رتبة 3). الجواب الوظيفي: 3.
مهمة 2. لتحديد عدد مستقلة خطيا صفوف من هذه المصفوفة.
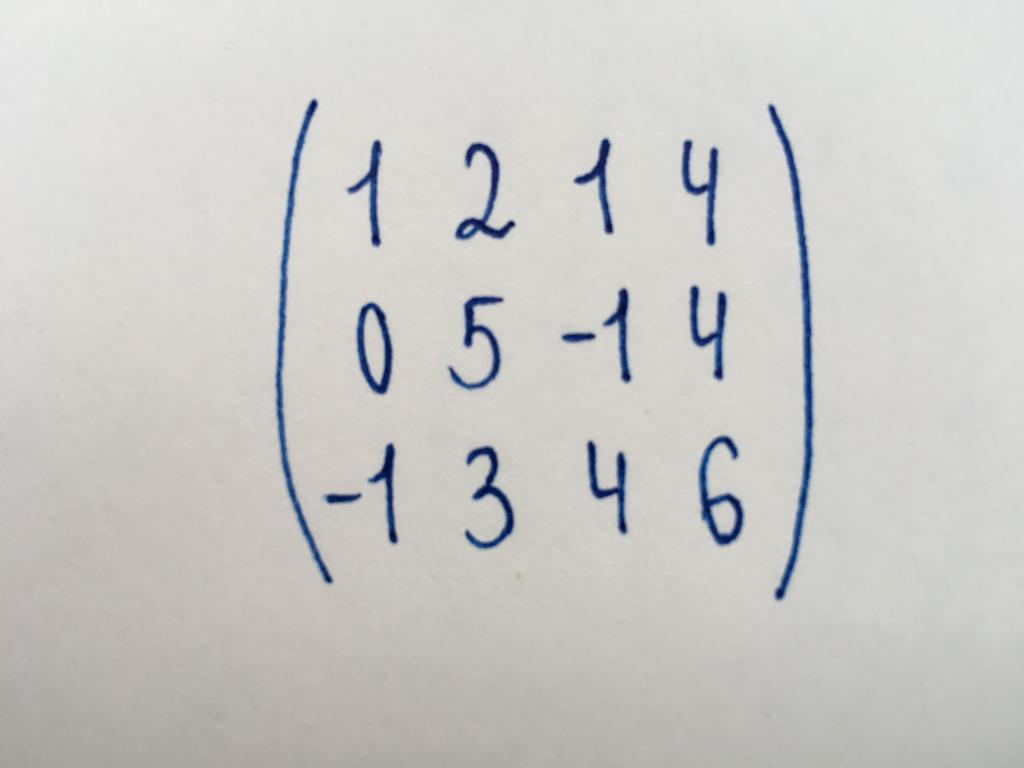
نحن بحاجة إلى العثور على السلاسل التي ليست أي التحولات لفت إلى الصفر. في الواقع نحن بحاجة إلى العثور على عدد غير صفرية الصفوف أو رتبة تمثل مصفوفة. للقيام بذلك, أداء التبسيط.
ونحن نرى المصفوفة التي لا تنتمي إلى نوع مربع. قد الأبعاد 3x4. دعونا نبدأ الزهر مع العنصر الزاوية اليسرى السفلى - عدد (-1).
إضافة األول إلى الصف الثالث. بجانب طرح الثانية إلى رسم عدد 5 إلى صفر.
تحويل مزيد من المستحيل. ومن هنا نستنتج أن عدد مستقلة خطيا الصفوف في الإجابة على المهمة 3.
الآن الحد من مصفوفة إلى سرعة البصر هو مهمة مستحيلة.
أمثلة من الوظائف ناقشنا الحد من مصفوفة على شكل الثلاثي ، صعدت المظهر. لجعل القيم المطلوبة صفر مصفوفة جداول في بعض الحالات قد تحتاج إلى إظهار الخيال بشكل صحيح تحويل هذه الأعمدة أو الصفوف. أتمنى لكم النجاح في الرياضيات و في العمل مع مصفوفة!
Article in other languages:

Alin Trodden - مؤلف المقال ، محرر
"مرحبا ، أنا ألين الدوس. أنا أكتب النصوص ، وقراءة الكتب ، والبحث عن الانطباعات. وأنا لست سيئة في أقول لك عن ذلك. أنا دائما سعيد للمشاركة في مشاريع مثيرة للاهتمام."
أخبار ذات صلة
البرقية أن كلمة قد تستحضر صورة المصفرة الرثة ورقة تتضمن الرسالة بعيدة عن بعض الأحداث التاريخية التي لا ترتبط ارتباطا وثيقا العالم الحديث. ومع ذلك, العديد من الطرق المستخدمة حاليا في الاتصالات ، يمكن اعتبار المباشرة أحفاد من البرقي...
الرياضة - بديلا عن العادات السيئة: دور الدوبامين
لماذا في السنوات الأخيرة تزايد شعبية نمط حياة صحي ؟ نوادي اللياقة البدنية, الأكل الصحي, و مختلف الإجراءات الرامية إلى تعزيز حيوية الجسم ، وأصبح ليس فقط الاتجاه المألوف. ما إذا كان من جهة, الرياضة – بدائل العادات الضارة ، ومن...
15-17 القرن ترك بصمة كبيرة في تاريخ الاقتصاد للبشرية جمعاء. في هذا العصر ، الاكتشافات الجغرافية الكبرى ، التي كانت شرطا أساسيا لتطور البرجوازية نمط الإنتاج. كانوا سبب في المقام الأول من خلال النمو النشط من القوى المنتجة في المجتمع...
مقال حول موضوع "الوطن" - كيفية كتابة الوطنية القصة ؟
تعلم كيفية كتابة مقال حول موضوع "الوطن" أن تخبر المعلمين قبل إعطاء طلاب هذه المهمة. وبصفة عامة ، كل شيء واضح ، ومع ذلك ، ما ينبغي أن يكون أسلوب ، وعلى وجه التحديد ما كنت بحاجة إلى أن أقول ؟ أن كل فهم.أهمية وشعبيةتجدر الإشارة إلى أ...
مدينة يابانية: أرض الشمس المشرقة ؟
معظم السلاف اعتبار أن ثقافة اليابان &ndash ؛ “السوشي ، كانجي كيمونو”. نظر ضيقة واحدة من أكثر البلدان المتقدمة يرتبط مع مستوى منخفض من الترويج. أنفسهم, ومع ذلك المحافظ اليابانيين يفضلون عدم الإعلان عن طريقتهم في الحياة ...
Lado Ketskhoveli: الحياة والموت الثوري
Lado Ketskhoveli كان واحدا من أهم أعضاء الحزب في منطقة ما وراء القوقاز. كان يعمل في أنشطة الطباعة والدعاية بين العاملات. معه في شبابه يعمل جوزيف ستالين. Ketskhoveli قتل خلال آخر بالسجن. عن البلاشفة ، أصبح نموذج البطل قدوة.أوائل سن...






















تعليقات (0)
هذه المادة قد لا تعليق أول