Матрицалардың түрлері. Сатылы түрі матрица. Келтіру матрица - ступенчатому және треугольному түрі

Матрицасы - бұл ерекше объект математика. Бейнеленеді түрінде тік бұрышты немесе квадрат кестелер, сложенной бірі-белгілі бір санының жолдарды және бағандарды. Математика бар, үлкен алуан түрлерін матрицаларды ерекшеленетін мөлшері бойынша немесе ұстау. Санының, оның жолдарды және бағандарды деп аталады тәртіптеріне. Бұл нысандар қолданылады математика реттеу үшін жазу сызықтық теңдеулер жүйесін және ыңғайлы іздеу олардың нәтижелері. Теңдеулер пайдалана отырып, матрица арқылы шешіледі әдісін Карл Гаусс, Габриэль Крамер, миноров және алгебралық толықтырулар, сондай-ақ көптеген басқа да тәсілдермен. Базалық қабілетіне кезінде оны есептеу келтіру болып табылады стандартты түрі. Алайда, бастау үшін талдап көрейікші, қандай матрицаларды бөледі математика.

Нөлдік түрі

Барлық компоненттері осы түрін матрица - нөлдер. Сонымен қатар, саны жолдар мен бағаналарды толығымен различно.

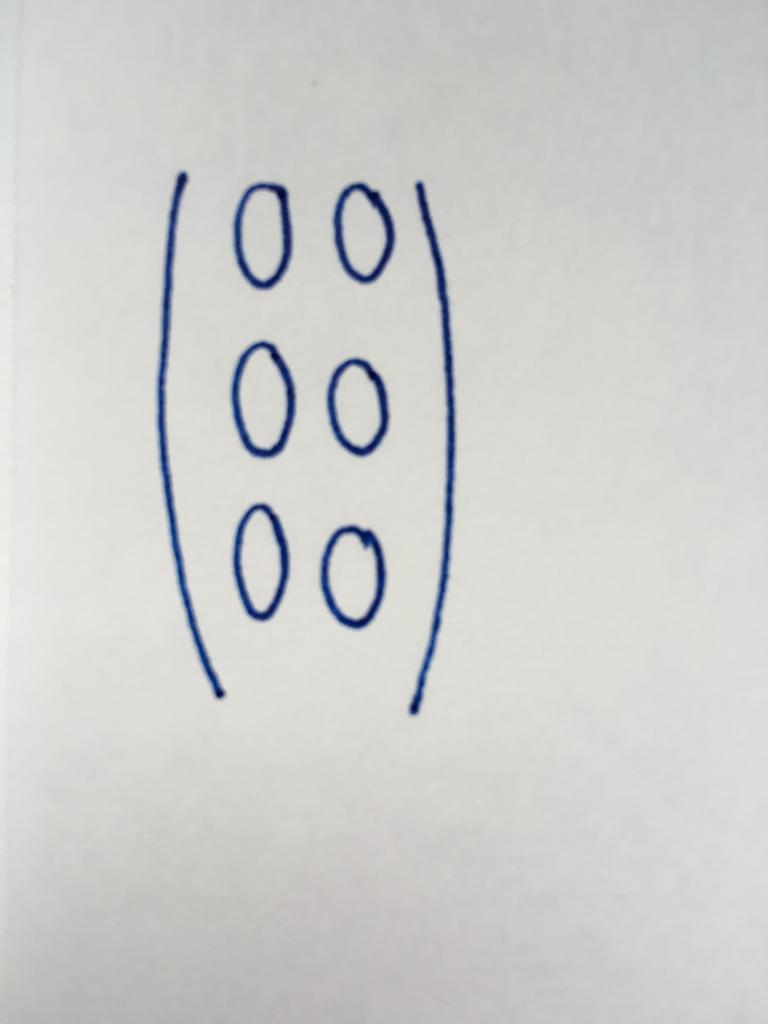
Шаршы түрі

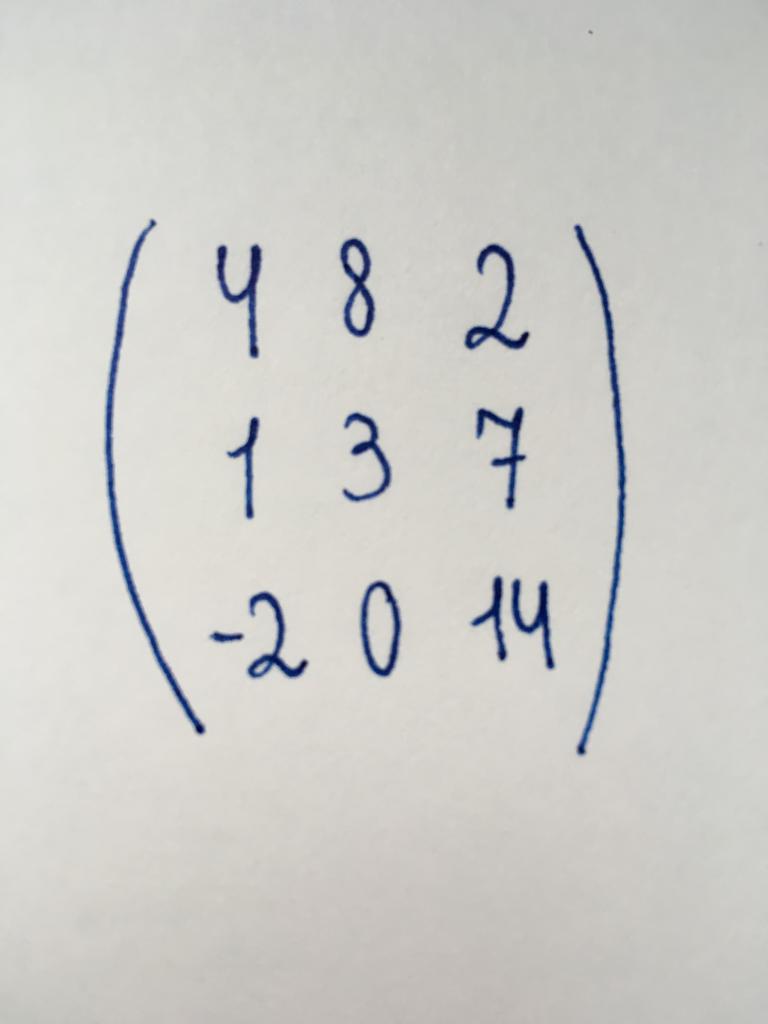
Саны баған және жолдан осы түрін матрица сәйкес келеді. Басқаша айтқанда, ол білдіреді кестені нысандары "квадрат". Саны баған (немесе жол) деп аталады тәртібі. Жеке жағдайлары болып саналады болуы матрицаның екінші ретті (2x2 матрица), төртінші (4x4), оныншы (10x10), он жетінші (17x17) және т.

Бағыты-стобец

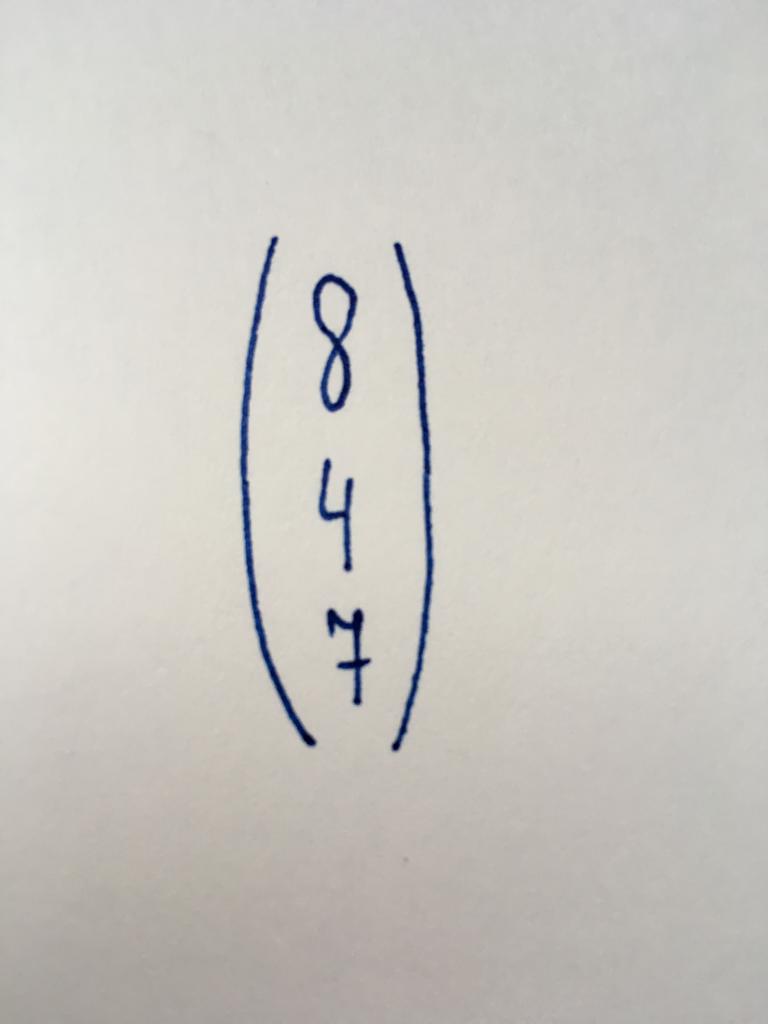
Бұл қарапайым түрлерін матрицаларды қамтитын тек бір баған, ол қамтиды үш сандық мәні. Ол ұсынады бірнеше бос мүшелерінің (сандар, тәуелсіз айнымалы) жүйелерінде желілік теңдеулер.

Вектор-жол

Түрі ұқсас алдыңғы. Үш сандық элементтер, өз кезегінде, ұйымдастырылған бір жолы.

Диагональды түрі

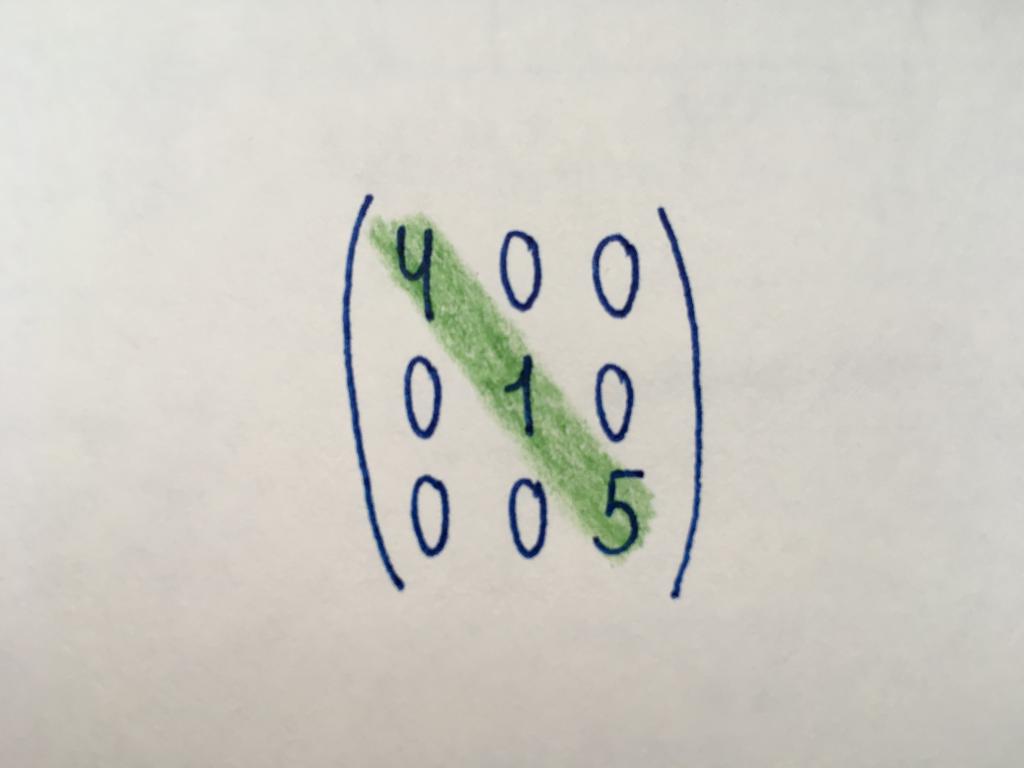
Сандық маңызы бар диагональном түріндегі матрица ғана қабылдайды компоненттері басты диагональ (бөлінген жасыл түспен). Негізгі диагональ басталады элемент орналасқан жоғарғы оң жақ бұрышында аяқталады санымен үшінші бағанда үшінші жол. Қалған компоненттері нөлге тең болады. Диагональды түрін білдіреді тек басқа тәсілмен бөлінген матрицасын қандай да бір тәртіп. Арасында матрицаларды қиғаш түрін бөліп көрсетуге болады скалярную. Оның барлық компоненттері қабылдайды бірдей маңызы бар.

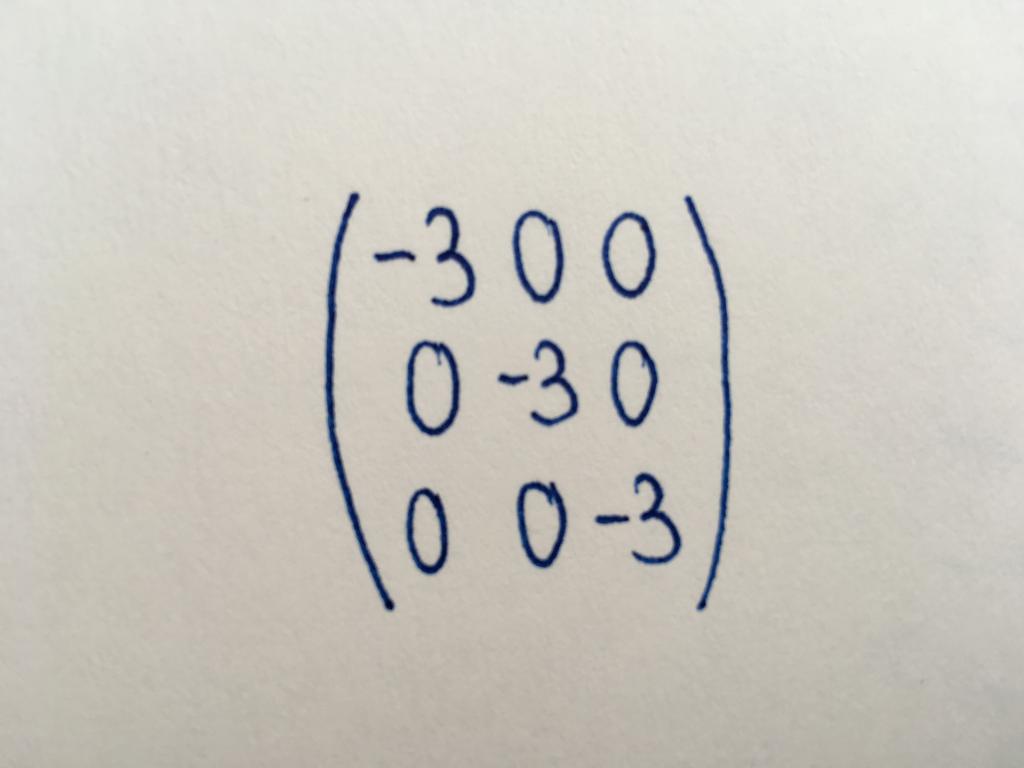
Бірлік матрица

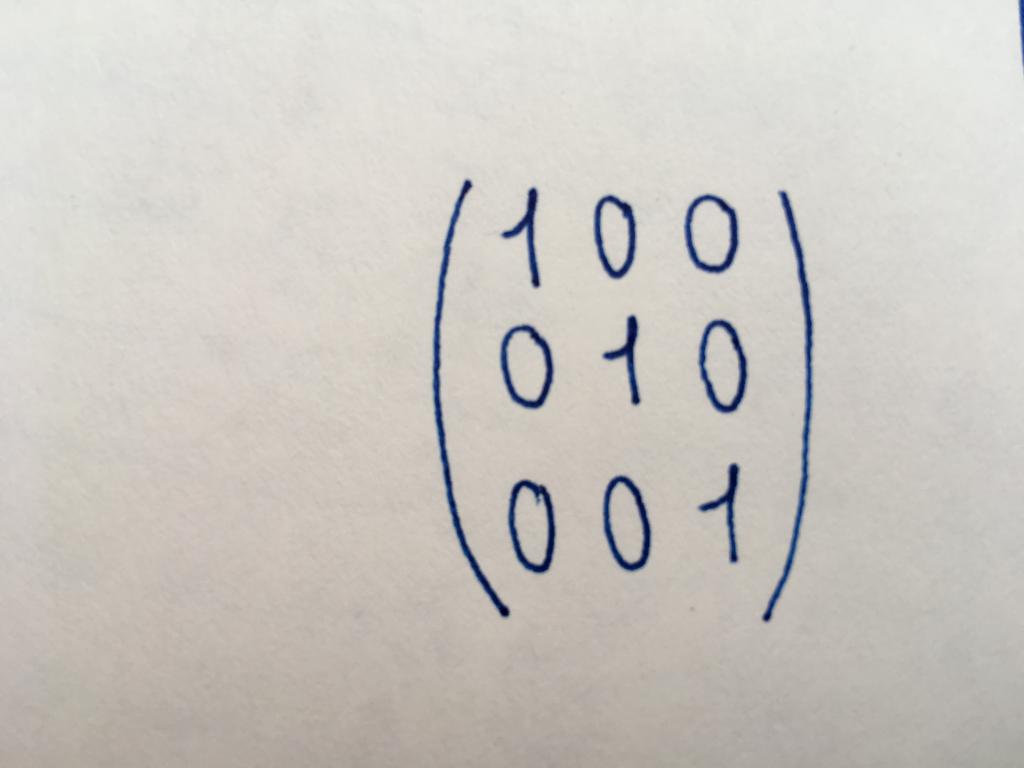
Кіші диагональды матрица. Оның сандық мәні болып табылады бірлік. Пайдалана отырып, жалғыз түрі матрицалық кесте орындайды, оның негізгі түрлендіру немесе матрицасын табады, кері бастапқы.

джентльменнің канондық түрі

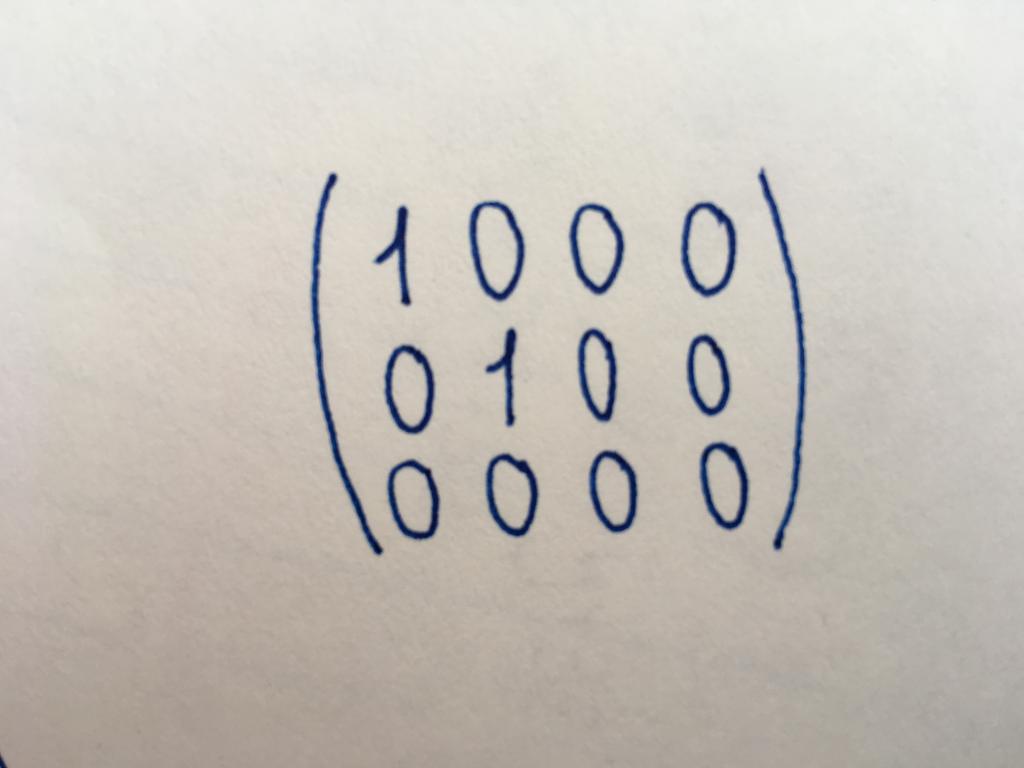
джентльменнің канондық түрі матрица бірі болып саналады; келтіру, оған жиі қажет. Жолдар мен бағандарды канонической матрицасы различно, ол міндетті түрде емес принадлежит к квадратному түрі. Ол бірнеше ұқсас единичную матрицасын, алайда оның барлық компоненттері негізгі диагональ қабылдайды мәні, тең бірлікте. Главнодиагональных бірлік болуы мүмкін екі, төрт (барлығы ұзындығы мен енін, матрицалар). Немесе бірлік болуы мүмкін емес, ойлауға, тіпті (ол деп саналады нөлдік). Қалған компоненттері канондық типті және элементтер қиғаш және бірлі-жарым, нөлге тең болады.

Үшбұрышты түрі

Бір маңызды түрлерін матрица қолданылатын іздеу кезінде оның детерминанта және орындау кезінде қарапайым операциялар. Үшбұрышты түрі қалай қиғаш, сондықтан матрица, сондай-ақ болып табылады төртбұрышты. Үшбұрышты матрица түрі бөлінеді верхнетреугольный және нижнетреугольный.

верхнетреугольной матрицасы (сур. 1) элементтері, олар үстінен бас диагоналі қабылдайды мәні нөлге тең. Компоненттері бір ең диагональ бөлігінде және матрицаны есептеудің оның астында, құрамында сандық мәндері.

нижнетреугольной (сур. 2), керісінше, элементтері, располагающиеся төменгі бөлігінде матрицалар, нөлге тең болады.

Сатылы матрица

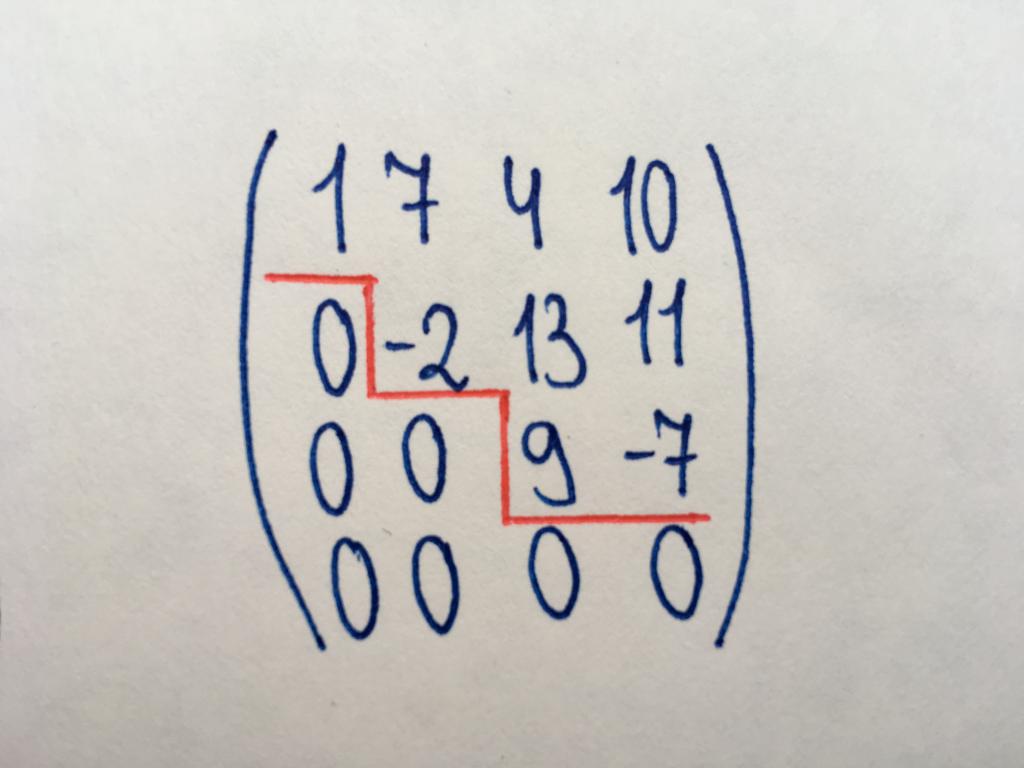
Түрі үшін қажет болған дәрежелі матрица, сондай-ақ үшін қарапайым іс-әрекеттердің олармен қатар үш бұрышты түрдегі). Сатылы матрица деп аталады, өйткені онда қамтылған тән "саты" нөлдердің (суретте көрсетілгендей). "Ступенчатом типі құрылады диагональ бірі нөлдердің (необязательно негізгі), және барлық элементтері астында осы диагоналі да мәні нөлге тең. Міндетті шарты болып табылады мынадай: егер сатылы матрицасы бар нөлдік жол болса, қалған жолдар орналасқан, одан төмен, сондай-ақ құрамында сандық мәндер.

осылайша, біз қарастырып, маңызды түрлері матрицаларды үшін қажетті олармен жұмыс істеу. Енді анықтаймыз міндеті түрлендіру матрица " талап етілетінболады.

Келтіру - треугольному түрі

Қалай келтіру матрицасын - треугольному түрі? Көбінесе тапсырмаларда қажет түрлендіру матрицасын в үшбұрышты түрі, табу үшін, оның детерминант, басқаша деп аталатын анықтауышы бар. Орындай отырып, осы рәсімді өте маңызды "сақтау" басты диагональ матрица, өйткені детерминант үшбұрышты матрицалар тең дәл осы шығармасы оның компоненттерін, басты диагональ. Еске сала кетейін, сондай-ақ баламалы әдістері болу определителя. Детерминант шаршы үлгідегі орналасқан арнайы формулалар. Мысалы, әдісін пайдалана үшбұрыш. Басқа матрицаларды қолданады ыдырату әдісі бойынша жол, бағана немесе олардың элементтері. Сондай-ақ, әдісін қолдануға миноров және алгебралық толықтырулар матрица.

Егжей-тегжейлі талқылайық келтіру процесі матрицалар - треугольному түрі үлгісінде кейбір тапсырмалар.

Тапсырма 1

табу Қажет детерминант ұсынылған матрица пайдалана отырып, әдісі келтіру треугольному түрі.

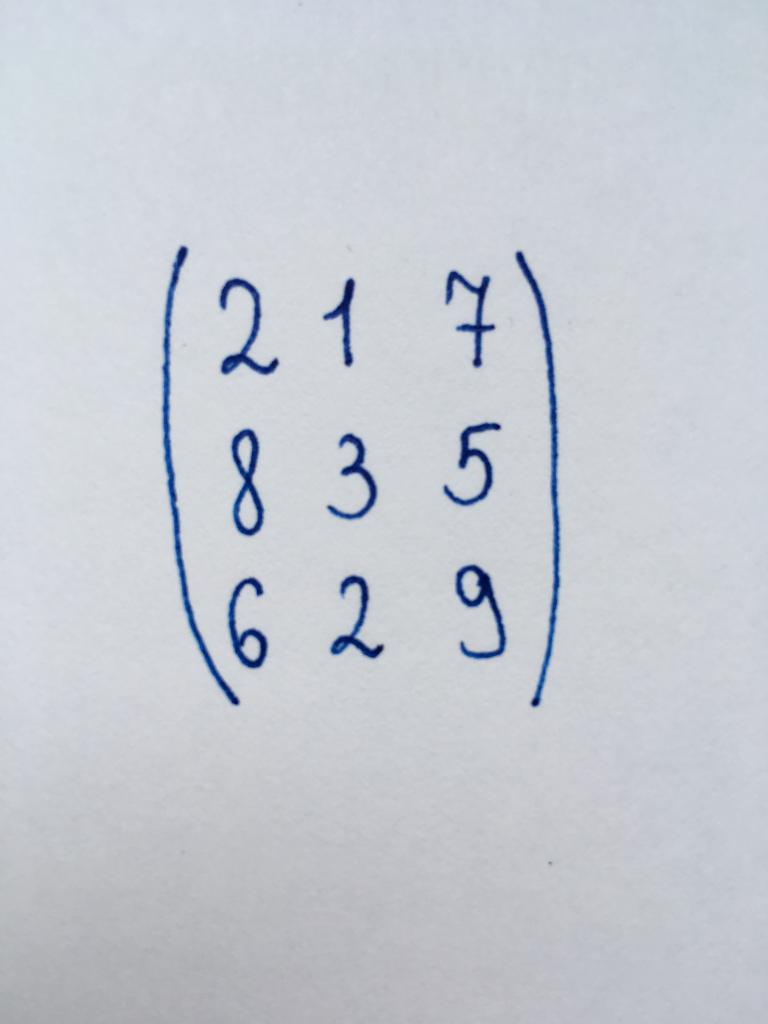
Бұл бізге матрица білдіреді басқа тәсілмен бөлінген матрицасын үшінші тәртібін. Демек, оны қайта құру треугольную нысанын бізге жан-нөл екі компонент бірінші бағанды және бір компонент екінші.

келтіру Үшін оны треугольному түрі, бастайық қайта сол жақтағы төменгі бұрышына матрицалар - айдың 6. Те оны нөл, умножим бірінші жолына үш және вычтем оны соңғы жол.

Маңызды! Жоғарғы жол өзгермейді, ал қалады, сол себепті бастапқы матрицасы. Жазу жолына, төрт есе үлкен бастапқы, қажет емес. Бірақ маңызы бар жолдарының, компоненттер қажет ететін азаматтарға нөл, үнемі өзгеріп отырады.

Бұдан әрі займемся келесі мәнді элементі - екінші жолдың бірінші бағанның, саны 8. Умножим бірінші жолы төрт және вычтем оның екінші жол. Аламыз нөл.

тек соңғы мәні - элемент үшінші жолдан екінші бағанды. Бұл саны (-1). Те оны нөл, бірінші жолдың вычтем екінші.

Орындаймыз тексеруді:

DetA = 2 x (-1) x 11 = -22.

Демек, бар тапсырма: -22.

Тапсырма 2

табу Керек детерминант матрица әдісімен келтіру треугольному түрі.

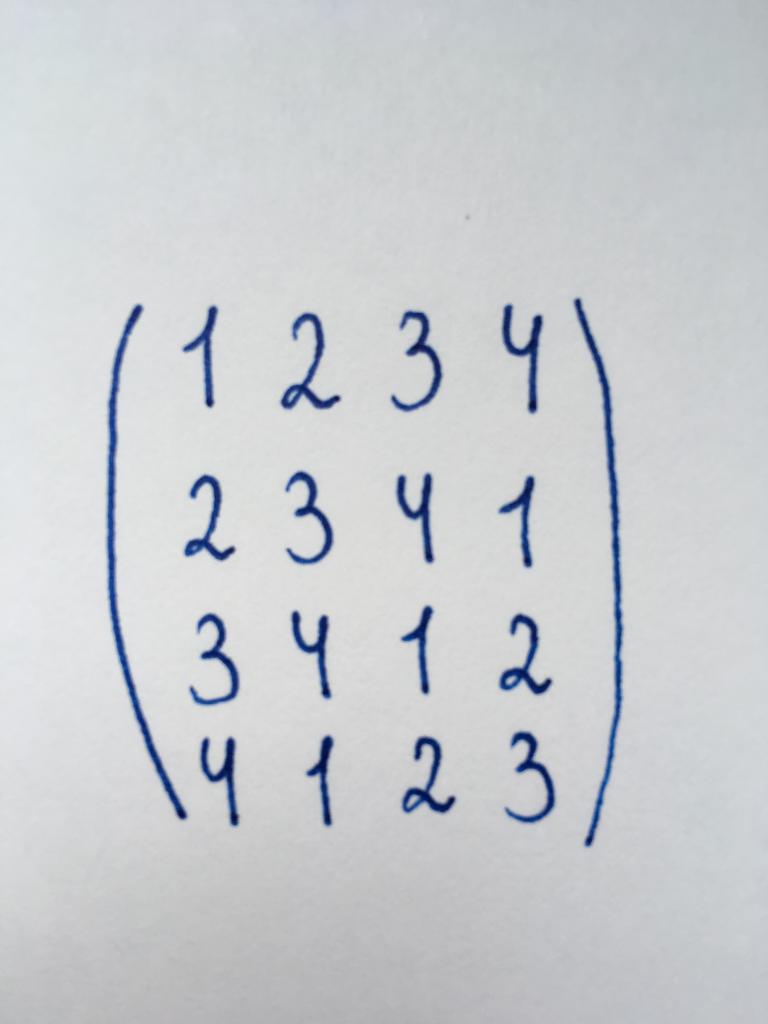
Ұсынылған матрица жатады квадратному түрі болып табылады матрицамен төртінші тәртібін. Демек, қажет нөлге түсіреді үш компонент бірінші бағанның, екі компонент екінші бағанды және бір компонент үшінші.

Бастаймыз келтіру, оны элемент орналасқан сол жақтың астыңғы бұрышында орналасқан, 4 санын. Бізге назар аудару бұл сан нөлге түсіреді. Ыңғайлы бұл, умножив төрт жоғарғы жолына, содан кейін шегеруге оны төртінші. Запишем бірінші кезеңінің түрлендіру.

Сонымен, компонент төртінші жолдың жеке және заңды тұлғалардың өтініштерін нөлге түсіреді. Енді бірінші элементі үшінші реттік санына 3. Орындаймыз ұқсас операция. Көбейтеміз үш бірінші жол, вычитаем оның үшінші жолдан записываем нәтижесі.

Бұдан әрі көріп саны 2 екінші жолда. Операцияны қайталаймыз: көбейтеміз жоғарғы мына екі және вычитаем оның екінші.

Бізге жан-нөл барлық компоненттер бірінші баған осы квадрат матрица қоспағанда, айдың 1 - элемент басты диагональ талап етпейтін түрлендіру. Енді сақтап, алынған нөлдер, сондықтан боламыз орындауға түрлендіру жолдармен, ал бағаналар. Енді екінші бағаны ұсынған матрица.

Қайтадан бастайық төменгі бөлігінде - элементтің екінші бағананың соңғы жолдың. Бұл сан (-7). Алайда, бұл жағдайда ыңғайлы бастау сандарды (-1) - элементтің екінші бағанның үшінші жол. Те оны нөл, вычтем үшінші жолдан екінші. Содан кейін умножим екінші жолына жеті және вычтем оны төртінші. Біз нөл орнына элемент орналасқан, төртінші жолда екінші бағанды. Енді көшсек, үшінші бағана.

осы бағанда бізге жан-нөл, бір ғана саны - 4. Мұны істеу қиын емес: жай прибавляем соңғы жолында үшінші көреміз бізге керекті нөл.

Кейін жүргізілген барлық өзгерістерді біз келтірді ұсынылған матрицасын - треугольному түрі. Енді табу үшін, оның детерминант, тек жүргізсін көбейту получившихся элементтері басты диагональ. Аламыз: DetA = 1 x (-1), x (-4) х 40 = 160. Сондықтан шешімімен саны болып табылады, 160.

Сонымен, енді сұрақ келтіру матрица - треугольному түрі сізге төлемақыны.

Келтіру - ступенчатому түрі

Кезінде қарапайым операциялар матрицалармен сатылы түрі болып табылады кем "сұранысқа ие" қарағанда, үшбұрышты. Көбінесе ол үшін пайдаланылады болу дәрежедегі матрица (т. е. саны, оның ненулевых жолдарының) немесе айқындау үшін сызықтық тәуелді және тәуелсіз жолдарының. Алайда сатылы матрица түрі болып табылады әмбебап, өйткені қолайлы ғана емес, шаршы типтес, бірақ және барлық қалған.

келтіру Үшін матрицасын - ступенчатому түрі, алдымен табу керек, оның детерминант. Бұл үшін подойдут жоғарыда аталған әдістер. Мақсаты болған детерминанта мынадай: анықтауға болады, түрлендіру және оны сатылы түрі матрица. Егер детерминант көп немесе аз нөл болса, онда асықпай кірісуге тапсырма. Егер ол нөлге тең, орындауға келтіру матрица - ступенчатому түрі жоқ. Мұндай жағдайда тексеру керек, жоқ па қате жазба немесе қайта құрулар матрица. Егер осындай дәлсіздіктер жоқ, тапсырмашешу мүмкін емес.

Қарастырамыз келтіру матрицасын - ступенчатому түрі үлгісінде бірнеше тапсырмалар.

Тапсырма 1. Табу дәрежесі осы матрицалық кесте.

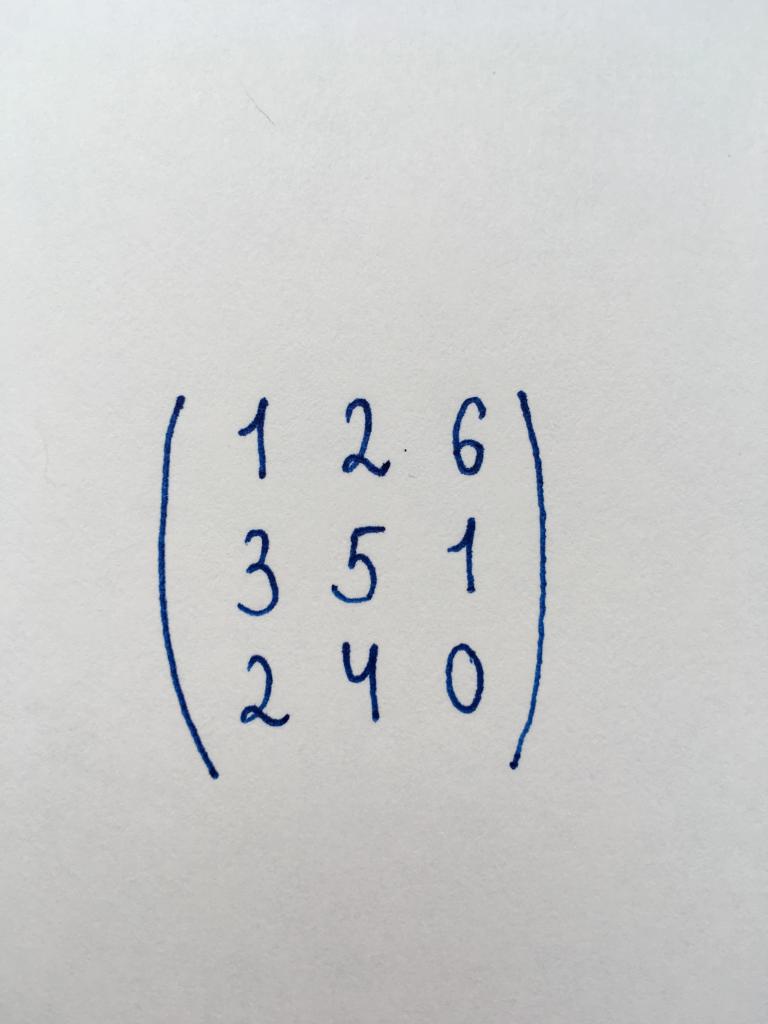
алдымызда анықталу облысы үшінші тәртібін (3x3). Біз білеміз, не үшін болу дәрежесінен келтіру қажет, оны ступенчатому түрі. Сондықтан алдымен бізге қажет табу детерминант матрица. Воспользуемся әдісімен үшбұрыш: DetA = (1-x 5 x 0) + (2 x 1 x 2) + (6 x 3 x 4) - (1-x 1-x 4) - (2 x-3 x 0) - (6 x 5 x 2) = 12.

Детерминант = 12. Ол нөлден жоғары болса, матрицасын келтіруге болады - ступенчатому түрі. Кірісеміз оны қайта құрулар.

Бастаймыз, оның элементінің сол жақ бағанның үшінші-жолдың - санының 2. Көбейтеміз жоғарғы мына екі және вычитаем оның үшінші. Осы операция ретінде бізге қажетті элементі, сондай-ақ саны 4 - элемент екінші бағанның үшінші-жолдың - жүгінді нөл.

Бұдан әрі аударамыз " нөл элементіне екінші жолдың бірінші баған - саны 3. Бұл үшін көбейтеміз жоғарғы мына үш және вычитаем оның екінші.

Біз көреміз, не келтіру салдарынан пайда болған үшбұрышты матрица. Біздің жағдайда жалғастыру өзгертуге болмайды, өйткені қалған компоненттері жоқ азаматтарға нөл.

Демек, жасаймыз деп қорытынды жолдардың саны бар сандық мәндері, осы матрицасы (немесе оның дәрежесі) - 3. Бар тапсырмасы: 3.

2 Тапсырма. Белгіленсін саны сызықтық тәуелсіз жолдар осы матрица.

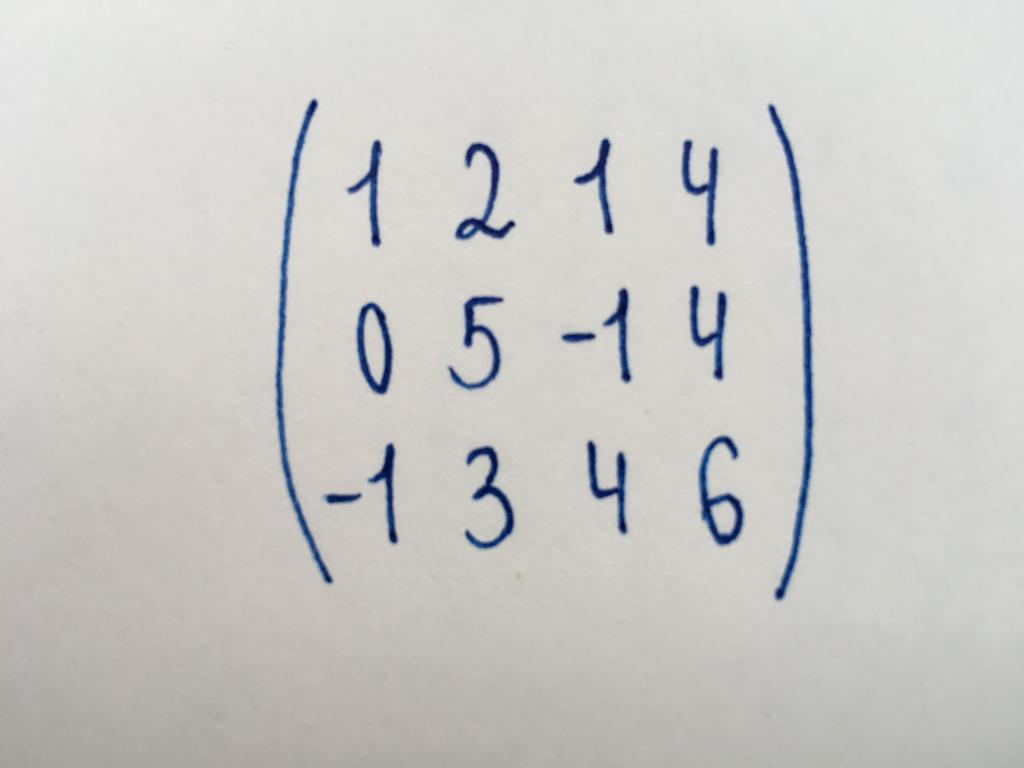
Бізге қажет табу жолының болмайтын қандай да бір өзгерістерге назар аудару нөлге түсіреді. Іс жүзінде бізге табуға саны ненулевых жолдарының, немесе дәрежесі ұсынылған матрица. Бұл үшін орындаймыз, оны жеңілдету.

Біз матрицасын, тиесілі - квадратному түрі. Ол өлшемі 3x4. Бастаймыз келтіру, сондай-ақ, элементтің сол жақ төменгі бұрышына - санының (-1).

Прибавляем бірінші жол үшінші. Бұдан әрі вычитаем одан екінші, обратить саны 5-нөл.

Одан әрі оны түрлендіру мүмкін емес. Демек, жасаймыз деп қорытынды саны сызықтық тәуелсіз жолдар, ол бар, тапсырма 3.

Енді келтіру матрица - ступенчатому түрі болып табылады, сіз үшін невыполнимым тапсырмаға сәйкес.

үлгісінде тапсырмаларды біз талдап келтіру матрица - треугольному түрі және ступенчатому түрі. Үшін азаматтарға нөл қажетті маңызы бар матрицалық кесте, жекелеген жағдайларда талап етіледі қиялдарын және дұрыс болып қайта құрылсын олардың бағандар немесе жолдар. Сәттілік сіздерге математика және жұмыс оны есептеу!