Now - 23:32:39
Equação irracional e suas soluções
Estudando álgebra, os alunos se deparam com equações de muitas espécies. Entre aqueles que são mais simples, pode ser chamado de linear, contendo uma desconhecida. Se a variável na matemática, uma expressão está sendo construído em um certo grau, então a equação é chamado quadrada, cúbica, биквадратным e assim por diante. As expressões podem conter números racionais. Mas há também uma equação irracional. Dos outros, eles diferem pela presença de funções, onde o desconhecido fica sob o sinal do radical (que é puro externamente a variável aqui você pode ver escrito sob a raiz quadrada). Solução de equações irracionais tem suas características. Ao calcular o valor da variável para obter a resposta correta, devem ser levadas em consideração.

“as Incontáveis palavras»
Não é segredo que os antigos matemáticos operado principalmente racionais números. Essas decisões incluem, como é conhecido, inteiros, expressas através ordinárias e decimais periódicos frações representantes dessa comunidade. No entanto, os cientistas Médio e Médio Oriente, Índia, desenvolvendo trigonometria, astronomia e álgebra, equação irracional também aprenderam a resolver. Por exemplo, os gregos sabiam similares em magnitude, mas, облекая-los em um cliente para atingir o formulário, usaram o conceito de "алогос", que significa "incontáveis". Um pouco mais tarde os europeus, imitando-lhes chamavam semelhantes o número de ão surdo". De todos os outros, eles diferem no fato de que só podem ser apresentadas em forma de infinito непериодической da fração final de uma expressão numérica que obter o impossível. Portanto, mais similares representantes do reino de números escritos na forma de números e caracteres como algum expressão, está sob a raiz do segundo ou maior grau.
Mais:
A história do desenvolvimento da tecnologia de computação
Os primeiros dispositivos de computação foram os próprios dedos de uma pessoa. Quando a ferramenta foi suficiente, no curso de iam pedras, galhos, conchas. Dobrando-se de um conjunto de dezenas, depois centenas, o homem aprendeu a contar e usar as fe...
O impulso nervoso, a sua conversão e o mecanismo de transmissão
O sistema Nervoso humano atua como uma espécie de coordenador no nosso corpo. Ela passa o comando do cérebro musculatura, órgãos, tecidos e processa os sinais de longo alcance deles. Como uma espécie de suporte de dados, é usado o impulso nervoso. O ...
Canal do panamá: um ano, a abertura oficial do objecto e a sua importância histórica
Durante séculos, a humanidade tenta recriar condições naturais da Terra, com o objetivo de receber quaisquer benefícios. Um desses casos, a adaptação é do canal do Panamá, o ano, a abertura oficial deste objeto foi marcado por um evento, повлиявшим p...
Com base No acima exposto, vamos tentar dar uma definição da equação irracional. Expressões similares contêm os chamados ão incalculável número" gravado usando o símbolo de raiz quadrada. Eles podem representar todos os tipos de bastante complexas opções, mas na sua наипростейшей forma têm essa aparência, como na foto abaixo.
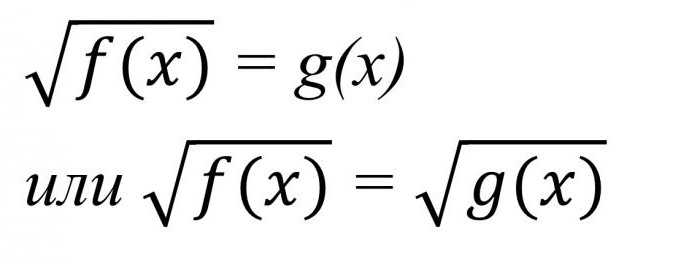
Преступая para resolver equações irracionais, as primeiras coisas primeiro é necessário calcular a área de valores da variável.
Faz sentido a expressão?
A Necessidade de verificação de valores decorre das propriedades da aritmética e a raiz quadrada. Como é sabido, semelhante a expressão é aceitável e tem qualquer sentido apenas quando determinadas condições. Em casos de raiz mesmo grau, todos подкоренные de expressão tem que ser positivo ou igual a zero. Se esta condição não for satisfeita, então apresentada uma gravação não pode ser considerada significativa.
Damos um exemplo concreto de como lidar com o irracional equação (foto abaixo).
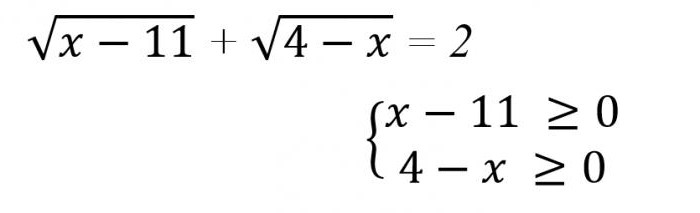
Neste caso, é evidente que as condições sob quaisquer valores recebidos cálculo do valor a ser executado não podem, assim, como é que 11 ≤ x ≤ 4. E, portanto, a solução pode ser apenas Ø.
O Método de análise
A Partir do descrito acima, torna-se claro como resolver a equação irracional de alguns tipos. Aqui um modo eficaz pode ser a simples análise.
Apresentamos uma série de exemplos, que, de novo, este é claramente demonstrar (foto abaixo).
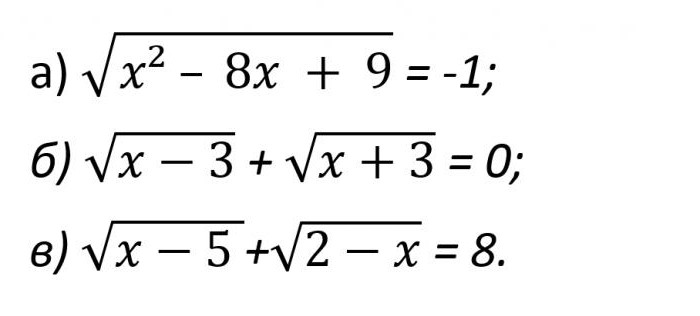
No primeiro caso, quando se olha mais de perto a expressão imediatamente parece bem claro que o verdadeiro ele não pode ser. Na verdade, no lado esquerdo da igualdade tem obtido um número positivo, que não é capaz de ser igual a -1.
No segundo caso, a soma dos dois positivos de expressão pode ser considerada igual a zero, apenas quando x - 3 = 0 e x + 3 = 0 ao mesmo tempo. E semelhante novamente é impossível. E então, em resposta, novamente, você deve escrever Ø.
O Terceiro exemplo é muito semelhante ao já considerado anteriormente. Na verdade, porque aqui as condições ОДЗ exigem, para que seja executada a seguinte absurda desigualdade: 5 ≤ x ≤ 2. E semelhante à equação da mesma forma, não pode ter sólidos de soluções.
Ilimitado aproximação
A Natureza irracional mais clara e completa pode ser explicada e realizada apenas através de uma interminável série de números decimal. Em específico, um exemplo brilhante de um dos membros desta família é o πи. Não sem razão, supõe-se que esta uma constante matemática era conhecida desde os tempos antigos, depois de ter sido usado na determinação de comprimentos de circunferência e área do círculo. Mas entre os europeus-la pela primeira vez aplicada na prática, o inglês William Jones e o suíço Leonhard Euler.

Ocorre esta constante da seguinte forma. Se compararmos os mais diferentes em torno da circunferência, a relação de seus comprimentos e diâmetros obrigatoriamente iguais para o mesmo número. Este é o πи. Se expressá-lo através de uma fração ordinária, cerca de recebermos a 22/7. A primeira vez que fiz isso, o grande Arquimedes, um retrato o qual é apresentado na figura acima. É por isso que é semelhante o número tem o seu nome. Mas não é explícita, e o valor aproximado de mal se não o mais surpreendente dos números. Um cientista brilhante, com uma precisão de até 0,02 encontrei num valor, mas, porverdade, essa constante não tem valor real, e é expressa como 3,1415926535… Ele representa um número infinito de dígitos, indefinidamente se aproximando de uma espécie de мифическому valor.
A Quadratura
Mas voltando à equação irracional. Para procurar desconhecido, neste caso, muito freqüentemente recorrem ao simples método: elevar ambas as partes disponíveis de igualdade ao quadrado. De forma semelhante, normalmente dá bons resultados. Mas deve-se considerar a conspiração irracional de valores. Todas essas raízes, você deve verificar, afinal, eles podem não ser compatíveis.
Mas, continuando a consideração de exemplos e tentar encontrar as variáveis novamente recomendada.
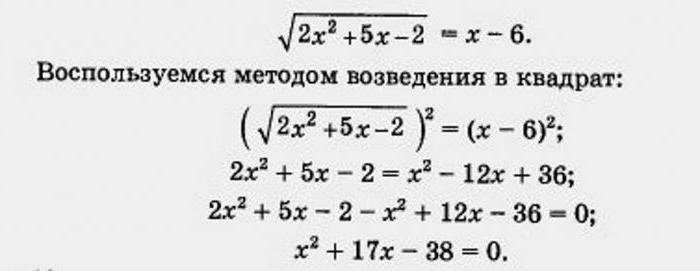
é um piscar de olhos, aplicando o teorema de Виета, encontrar os valores depois em conseqüência de determinados оперций formamos uma equação quadrática. Aqui o resultado é que entre as raízes são 2 e -19. No entanto, ao verificar, substituindo o valor recebido no original a expressão, pode ter certeza que nenhuma dessas raízes não é adequado. É um fenômeno freqüente no equações irracionais. Isso significa que o nosso dilema de novo, não tem soluções, e a resposta deve especificar um conjunto vazio.
Exemplos de посложней
Em alguns casos, é necessário um quadrado de ambas as partes de uma expressão, não uma, mas várias vezes. Vamos analisar um exemplo, onde é necessário. Pode ver abaixo.
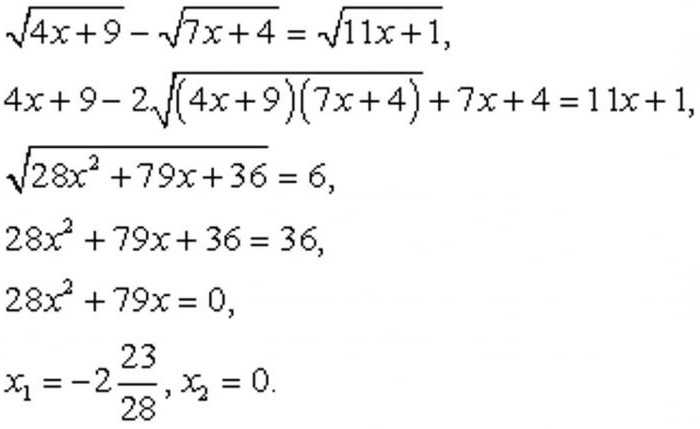
Com as raízes, não se esqueça de verificar a sua, porque podem ocorrer em excesso. Deve-se explicar, por que é que isso é possível. Quando a aplicação deste método ocorre em alguma forma de racionalização de uma equação. Mas se livrar da indesejada nós de raízes, que o impedem de produzir operações aritméticas, como se expandindo existente área de valores, o que pode ser (como você pode entender a) conseqüências. Antecipando semelhante, nós produzimos a verificação. Neste caso, tem a chance de se certificar de que é adequado apenas uma das raízes: x = 0.
O Que fazer em casos em que é necessário realizar a solução de sistemas de equações irracionais, e temos em estoque, não apenas uma, mas duas desconhecidas? Aqui fazemos assim como, em casos normais, mas tendo em conta o acima de propriedades de dados de expressões matemáticas. E a cada nova tarefa, é claro, deve-se aplicar uma abordagem criativa. Mas, novamente, é melhor considerar todos em um exemplo específico, apresentado a seguir. Aqui não é apenas necessário encontrar as variáveis x e y, mas para apontar a resposta a sua soma. Então, existe um sistema que contém irracional magnitude (см. foto abaixo).

Como você pode ver, essa tarefa não é nada sobrenatural complexa. Só necessita de mostrar inteligência e acho que a parte da esquerda da primeira equação representa o quadrado da soma. Essas tarefas são encontrados em PÚBLICO.
Irracional na matemática
Cada vez que a necessidade de criação de novos tipos de números de gerar um ser humano quando ele não tinha "espaço" para soluções de algumas equações. Irracionais os números não são excepção. Como mostram os fatos da história, pela primeira vez, os grandes sábios chamaram a atenção mesmo antes de nossa era, no século VII. Fiz isso matemático da Índia, conhecido sob o nome de Манава. Ele claramente entendeu que, a partir de alguns dos números naturais não é possível extrair a raiz. Por exemplo, a decisões incluem 2; 17 e 61, bem como muitos outros.
Um dos пифагорейцев, o pensador de nome Гиппас, chegou à mesma conclusão, tentando fazer cálculos com as expressões numéricas lados do pentagrama. Abrindo a matemática os itens que não podem ser expressas por valores numéricos e não têm propriedades comuns de números, ele é tão irritou um de seus colegas, o que foi jogado fora depois de bordo de um navio, no mar. O fato é que outros пифагорейцы achou que o seu raciocínio motim contra as leis do universo.
O Sinal do radical: a evolução
O Sinal de raiz para a expressão do valor numérico ão de surdos» números começou a ser utilizado na solução de inequações irracionais e equações para longe imediatamente. Pela primeira vez sobre радикале começaram a pensar europeus, especialmente italianos, matemática, aproximadamente, no século XIII. Então para se referir inventou o ciclismo américa latina, R. Mas os alemães da matemática em seus trabalhos o fizeram. Mais gostei da letra V. Na alemanha, logo se espalhou a designação de V(2) V(3), que se destina a era expressar a raiz quadrada de 2, 3 e assim por diante. Mais tarde, em caso de interveio нидерландцы e видоизменили o sinal do radical. E completou a evolução de René Descartes, trazendo o sinal da raiz quadrada e o moderno de excelência.

A Libertação do irracional
Irracional equações e inequações podem incluir a variável não só sob o signo de uma raiz quadrada. Ele pode ser de qualquer grau. A forma mais comum de se livrar dele é a possibilidade de construir a ambas as partes a igualdade no nível apropriado. É a principal ação para ajudar em operações com irracionais. Ações em diferentes ocasiões, especialmente, não são diferentes daqueles que já foram analisados anteriormente. Aqui devem ser consideradas as condições de неотрицательности digitar caracteres, e no final uma solução, é necessário produzir o abandono de valores estranhosvariável, desta forma, como foi mostrado na discutido já exemplos.
A Partir de adicionais de transformação, que o ajudarão a encontrar a resposta correta, muitas vezes, é usada a multiplicação de expressões emocionais, bem como, muitas vezes, é necessária a introdução de uma nova variável, o que facilita a decisão. Em alguns casos, para encontrar o valor desconhecido, é apropriado para aplicar gráficos.
Article in other languages:
AR: https://tostpost.com/ar/education/15212-irrational-equations-and-their-solutions.html
BE: https://tostpost.com/be/adukacyya/26336-racyyanal-nyya-ra-nenn-sposaby-h-vyrashennya.html
DE: https://tostpost.com/de/bildung/26008-gleichungen-irrationale-und-deren-l-sungen.html
En: https://tostpost.com/education/25951-irrational-equations-and-their-solutions.html
ES: https://tostpost.com/es/la-educaci-n/25909-ecuaciones-irracionales-y-sus-soluciones.html
HI: https://tostpost.com/hi/education/14969-irrational-equations-and-their-solutions.html
JA: https://tostpost.com/ja/education/14925-irrational-equations-and-their-solutions.html
KK: https://tostpost.com/kk/b-l-m/26603-irracional-te-deuler-zh-ne-olardy-sheshu-t-s-lder.html
PL: https://tostpost.com/pl/edukacja/27666-r-wnania-irracjonalne-i-sposoby-ich-rozwi-zania.html
TR: https://tostpost.com/tr/e-itim/26540-denklemler-mant-ks-z-ve-z-mleri.html
UK: https://tostpost.com/uk/osv-ta/26884-rrac-onal-n-r-vnyannya-ta-sposobi-h-vir-shennya.html
ZH: https://tostpost.com/zh/education/5874-irrational-equations-and-their-solutions.html

Alin Trodden - autor do artigo, editor
"Olá, sou o Alin Trodden. Escrevo textos, leio livros e procuro impressões. E eu não sou ruim em falar sobre isso. Estou sempre feliz em participar de projetos interessantes."
Notícias Relacionadas
Qual é o nome do Einstein? O que é um Einstein?
a Genialidade do famoso física-teórico А. Einstein deu mundial de glória durante a vida. Depois de sessenta anos depois de sua morte, o mundo ainda admira a profundidade de teorias e coragem pressupostos do cientista.no Entanto, c...
O conceito de Cultura na Sociologia
o Termo cultura caracterizada pela ambiguidade e é usada para o definição de processos espiritual, intelectual, estético de desenvolvimento; formas e produtos espiritual, intelectual e atividades artísticas; descrever ...
Incolor viscoso líquido, a temperatura de ebulição, que é de 269,2 º, e a densidade de 1,83 g/ml quando a temperatura ambiente (20º) – este é o ácido sulfúrico. A temperatura de fusão da substância é igual a 10,3&o...
a Era do palácio de golpes 1725-1762 гг. – тридцатисемилетний fase de instabilidade política, que começou após a morte de Pedro I. Palácio saber образовавшая agrupamento, interveio ativamente na política do país. A sol...
o Hidrogênio amplamente utilizados nos mais diversos setores: na síntese de хлорводорода, amônia (amoníaco é usado para a produção de fertilizantes à base de nitrogênio), em анилинокрасочном produção, ao restaurar a partir de miné...
Ao que temperatura a água congela e outros fatos interessantes
Se você perguntar para uma pessoa: "ao que temperatura a água congela?", então, mais frequentemente, vamos ouvir a resposta, que é de 0 graus Celsius. No entanto, não é sempre assim. Por exemplo, se lentamente refrigerar...




















Comentários (0)
Este artigo possui nenhum comentário, seja o primeiro!