Now - 12:46:47
Równania irracjonalne i sposoby ich rozwiązania
Podczas Nauki algebry, uczniowie borykają się z równań wielu gatunków. Wśród tych z nich, które najbardziej proste, można nazwać liniowe zawierające jedną niewiadomą. Jeśli zmienna w wyrażeniu matematycznym budowany w pewnym stopniu, to równanie nazywane jest kwadratowy, sześcienny, биквадратным i tak dalej. Podane wyrażenia mogą zawierać liczby wymierne. Ale istnieją również równania irracjonalne. Od innych różnią się obecnością funkcji, gdzie nieznane jest pod znakiem grupy funkcyjnej (czyli czysto zewnętrznie zmienną można tu zobaczyć napisanej pod kwadratowym korzeniem). Rozwiązanie irracjonalnych równań ma swoje charakterystyczne cechy. Przy obliczaniu wartości zmiennej dla uzyskania właściwej odpowiedzi należy koniecznie wziąć pod uwagę.

«Niezliczone słowy»
Nie jest tajemnicą, że starożytni matematycy operowali głównie racjonalne liczbami. Należą do nich, jak wiadomo, całe, wyrażający się poprzez zwykłe i dziesiętne ułamki okresowe przedstawiciele tej społeczności. Jednak naukowcy i Bliskiego Wschodu, a także w Indiach, rozwijając trygonometrycznymi, astronomii i algebry, irracjonalne równania też uczyli się rozwiązywać. Na przykład, grecy wiedzieli podobne wartości, ale облекая ich w formę werbalną, używali pojęcie «алогос», co oznacza, że «niezliczone». Nieco później europejczycy, naśladując ich, nazywali takie numery «głuche». Od pozostałych różnią się tym, że mogą być składane tylko w formie nieskończonej непериодической ułamki, ostateczna wartość liczbowa, której uzyskanie jest po prostu niemożliwe. Dlatego częściej podobne przedstawiciele królestwa liczby zapisywane są w postaci cyfr i znaków jak jakiś wyraz, znajdujące się pod korzeniem drugi lub większym stopniu.
Bardziej:
Główne etapy rozwoju psychiki w филогенезе
Rozwój psychiki w филогенезе charakteryzuje się kilkoma etapami. Rozważmy dwie główne historie związane z tym procesem.Филогенез - to historyczny rozwój, obejmującego miliony lat ewolucji, historię rozwoju różnych gatunków organizmów żywych.Ontogenez...
Co to jest gronkowiec i metody jego leczenia
Wielu w swoim życiu miał do czynienia z zakażeniem gronkowca. Dlatego konieczne jest posiadanie pełnej informacji o tej chorobie, aby w pełni zrozumieć, co dzieje się w organizmie. Więc co to jest gronkowiec? To bakterie, lub jedną z ich odmian, z kt...
Przed podjęciem się, że studiuje morfologia, należy zauważyć, że sam studiuje ten dział gramatyki. Tak, morfologia studiuje słowo jako część mowy, a także sposoby jego edukacji, jego formy, struktury i gramatyki wartości, a także poszczególne j...
Na podstawie powyższego spróbujmy zdefiniować иррациональному równanie. Podobne wyrażenia zawierają tak zwane „niezliczone liczby», nagrane z użyciem znaku pierwiastka kwadratowego. Mogą stanowić różnego rodzaju dość skomplikowane opcje, ale w swojej наипростейшей formie mają taki widok, jak na zdjęciu poniżej.
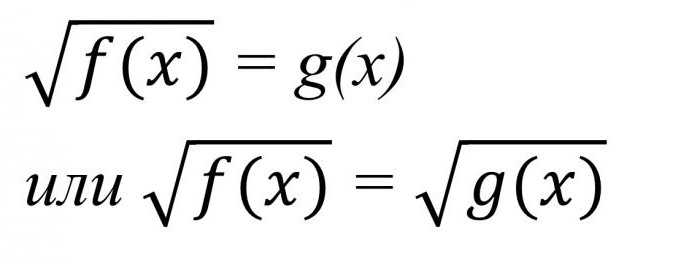
Przekraczanie do rozwiązania irracjonalnych równań, na początek należy obliczyć obszar dopuszczalnych wartości zmiennej.
Czy Ma sens wyrażenie?
Konieczność weryfikacji uzyskanych wartości wynika z właściwości arytmetyczne pierwiastka kwadratowego. Jak wiadomo, taki wyraz przyjęcia i ma sens tylko w określonych warunkach. W przypadkach korzenia stopnia parzystego wszystkie подкоренные wyrażenia muszą być dodatnia lub równa zero. Jeśli ten warunek nie jest spełniony, to przedstawione matematyczny zapis nie może być uznane za znaczące.
Oto konkretny przykład, jak rozwiązywać irracjonalne równania (na zdjęciu poniżej).
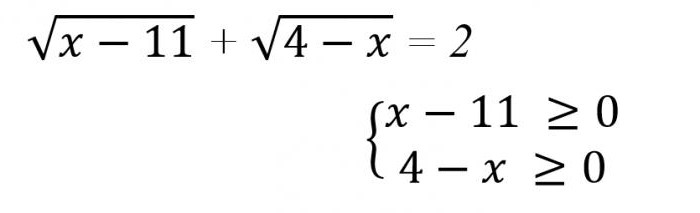
W tym przypadku jest oczywiste, że te warunki w żadnych wartościach przyjmowanych poszukiwanej wielkości, wykonywane nie mogą, tak jak okazuje się, że 11 ≤ x ≤ 4. A to znaczy, że rozwiązaniem może być tylko Ø.
Metoda analizy
Z powyższego staje się jasne, jak rozwiązywać irracjonalne równanie niektórych typów. Tutaj skutecznym sposobem może okazać się prosty test.
Oto kilka przykładów, które ponownie dobitnie to pokazują (na zdjęciu poniżej).
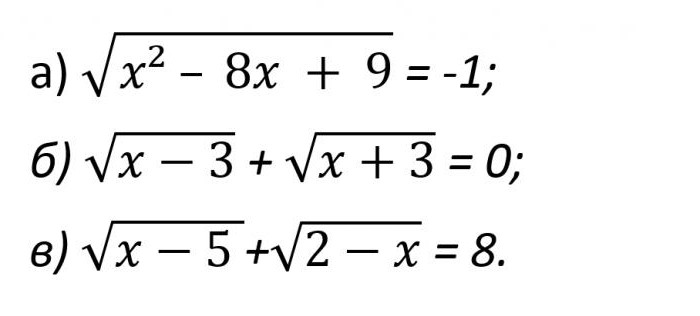
W pierwszym przypadku, przy uważnym przyjrzeniu wyrażenia raz okazuje się jasne, że prawdziwym ono być nie może. Naprawdę, ponieważ po lewej stronie równości powinno uzyskać liczbę dodatnią, która w żaden sposób nie może być równy -1.
W drugim przypadku suma dwóch pozytywnych wyrażeń może być równa zero, jedynie tylko wtedy, gdy x - 3 = 0 i x + 3 = 0 jednocześnie. A takie znowu niemożliwe. I to znaczy, że w odpowiedzi ponownie należy pisać Ø.
Trzeci przykład jest bardzo podobny do już wspomniany wcześniej. Naprawdę, ponieważ warunki GBP wymagają, aby uruchamiać następujący absurdalne nierówność: 5 ≤ x ≤ 2. A takie równanie w podobny sposób w żaden sposób nie może mieć rozsądnych decyzji.
Nieograniczona przybliżenie
Przyroda irracjonalnego najbardziej jasne i w pełni może być wyjaśnione i poznana tylko przez niekończący się ciąg liczb po przecinku. A konkretnym, żywym przykładem z członków tej rodziny jest πi. Nie bez powodu zakłada się, że ta matematyczna stała znana była od czasów starożytnych, используясь przy obliczaniu długości obwodu i powierzchni koła. Ale wśród europejczyków ją po raz pierwszy zastosowali w praktyce anglik William Jones i szwajcar Leonard Euler.

Występuje ta stała się w następujący sposób. Jeśli porównać różne długości okręgu, to stosunek ich długości i średnic obowiązkowo są równe tej samej liczby. To jest πi. Jeśli wyrazić go przez zwykły śrut, to otrzymamy w przybliżeniu 22/7. Po raz pierwszy zrobił wielki Archimedes, którego portret jest przedstawiony na rysunku powyżej. Dlatego takiego liczba otrzymało jego imię. Ale to nie jest bezpośrednia, a przybliżoną wartość bodaj czy nie najbardziej zaskakujące z liczb. Genialny naukowiec z dokładnością do 0,02 znalazł poszukiwaną wielkość, alerzeczywistości, ta stała nie ma realnej wartości, a wyraża się jak 3,1415926535… Jest to nieskończony szereg cyfr, bez ograniczeń zbliżając się do jakiegoś mitycznego wartości.
Podnoszenie do kwadratu
Ale wracając do irracjonalne równania. Aby znaleźć nieznane, w tym przypadku bardzo często uciekają się do prostej metody: budują obie części istniejącej równości do kwadratu. W podobny sposób zwykle daje dobre wyniki. Ale należy wziąć pod uwagę spryt irracjonalnych wartości. Wszystkie otrzymane w wyniku tego korzenie trzeba sprawdzać, bo oni mogą nie działać.
Ale dalej rozpatrzenie przykładów i postaramy się znaleźć zmienne nowo proponowanego sposób.
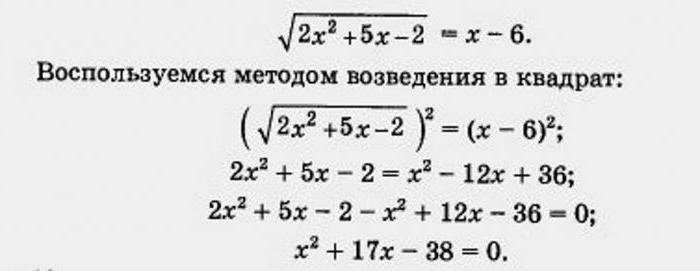
Bardzo proste, stosując twierdzenie Виета, znaleźć szukane wartości po tym, jak w wyniku pewnych po wielu operacjach plastycznych u nas powstało równanie kwadratowe. Tutaj okazuje się, że wśród korzeni będą 2 i -19. Jednak podczas sprawdzania, po wprowadzeniu otrzymane wartość początkowa wyrażenie, można upewnić się, że żaden z tych korzeni nie pasuje. To częste zjawisko w irracjonalnych równaniach. To znaczy, że nasz dylemat znów nie ma rozwiązań, a w odpowiedzi należy podać zbiór pusty.
Przykłady miejsce
W niektórych przypadkach wymagane jest budować w kwadrat obie części wyrażenia nie jeden, a kilka razy. Rozważmy przykłady, gdzie wymagana jest określona. Można je zobaczyć poniżej.
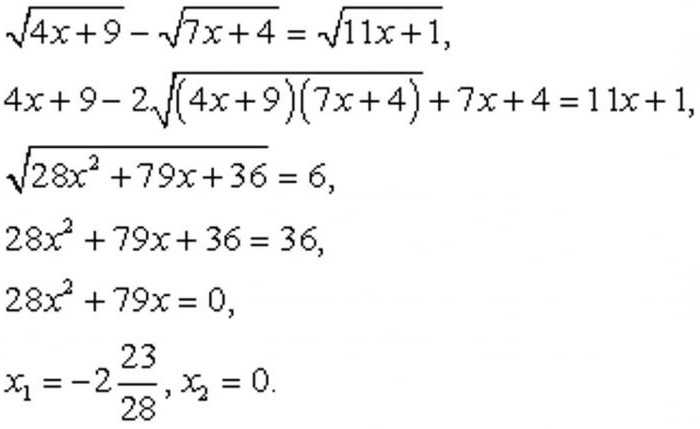
Po Otrzymaniu korzenie, nie zapominamy ich sprawdzać, bo mogą pojawić się niepotrzebne. Należy wyjaśnić, dlaczego jest to możliwe. Przy stosowaniu takiej metody dzieje się w pewnym sensie racjonalizacja równania. Ale pozbywając się niewygodnych dla nas korzeni, które uniemożliwiają produkować działań arytmetycznych, jak gdyby rozszerzyć istniejący obszar wartości, co skutkuje (jak można zrozumieć) konsekwencjami. Przewidując takiego, my wykonujemy test. W tym przypadku istnieje szansa, aby upewnić się, że pasuje tylko jeden z korzeni: x = 0.
System
Co robić w przypadkach, gdy jest to wymagane do przeprowadzenia rozwiązanie systemów irracjonalnych równań, i u nas w magazynie nie jeden, a aż dwa nieznane? Tutaj postępujemy tak samo, jak w typowych przypadkach, ale z uwzględnieniem powyższych właściwości danych wyrażeń matematycznych. I w każdym nowym zadaniu, oczywiście, należy stosować kreatywne podejście. Ale znowu, lepiej jest rozważyć wszystkie na konkretnym przykładzie przedstawionym poniżej. Tutaj nie po prostu chcesz znaleźć zmienne x i y, ale i wskazać w odpowiedzi na ich sumę. Tak więc, jest to system, zawierający irracjonalne wartości (patrz zdjęcie poniżej).

Jak można upewnić się, takie zadanie nie jest niczym dziwnym skomplikowanego. Wymagane jest tylko, aby pokazać pomysłowość i domyślić się, że lewa część równania pierwszego jest kwadrat sumy. Zadania te znajdują się w EGE.
Nieracjonalne z matematyki
Za Każdym razem potrzeba tworzenia nowych rodzajów liczb występował u ludzkości wtedy, gdy brakowało mu «przestrzeni» dla rozwiązania pewnych równań. Nieracjonalne liczby nie są wyjątkiem. Jak świadczą fakty z historii, po raz pierwszy wielcy mędrcy zwrócili na to uwagę jeszcze przed naszą erą, w wieku VII. Zrobił to matematyk z Indii, znany pod nazwą Манава. On dobrze rozumiał, że z niektórych liczb naturalnych nie można wyciągnąć pierwiastek. Na przykład, należą do nich 2; 17 lub 61, a także wiele innych.
Jeden z пифагорейцев, myśliciel o imieniu Гиппас, doszedł do tego samego wniosku, starając się obliczeniowych liczbowe wyrażeń stron pentagramu. Otwierając matematyczne elementy, które nie mogą być wyrażone wartościami i nie mają właściwości zwykłych liczb, to jest tak, że swoich kolegów, że został wyrzucony za burtę statku w morze. Rzecz w tym, że inne пифагорейцы uznali, że jego rozumowanie jest buntem przeciwko praw wszechświata.
Znak grupy funkcyjnej: ewolucja
Znak korzenia do wyrażenia wartości liczbowej «głuchych» liczb był wykorzystywany przy rozwiązywaniu irracjonalnych nierówności i równań daleko nie raz. Po raz pierwszy o радикале zaczęli się zastanawiać europejskie, w szczególności włoskie, matematyki, około XIII wieku. Wtedy też dla oznaczenia wymyślili wykorzystać ameryki łacińskiej R. Ale niemieccy matematycy w swoich pracach postępowali inaczej. Im więcej się podobała litera V. W niemczech wkrótce rozprzestrzenił się oznaczenie V(2) V(3), który został zaprojektowany, aby było wyrażać pierwiastek kwadratowy z 2, 3 i tak dalej. Później w sprawę zaangażował нидерландцы i przebudowano znak grupy funkcyjnej. A zakończył ewolucję Rene Descartes, doprowadzając znak pierwiastka kwadratowego do współczesnego doskonałości.

Wybawienie od irracjonalnego
Irracjonalne równania i nierówności mogą zawierać zmienną nie tylko pod znakiem pierwiastka kwadratowego. Może być o dowolnym stopniu. Najbardziej popularnym sposobem, aby pozbyć się go jest możliwość podnieść obie części równości w odpowiedni stopień. Jest to podstawowa czynność, która pomaga przy operacjach z irracjonalne. Działania w parzystych przypadkach szczególnie nie różnią się od tych, które zostały już zaakceptowane przez nas wcześniej. Tutaj powinny być uwzględnione warunki неотрицательности подкоренного wyrażenia, a także po zakończeniu rozwiązania należy przeprowadzać pokazy obcych wartościzmiennych w taki sposób, jak zostało to pokazane w omówionych już przykładach.
Z dodatkowych przekształceń, które pomagają znaleźć właściwą odpowiedź, często używane wyrażenia mnożenie na powiązane, a także często wymagane jest wprowadzenie nowej zmiennej, co ułatwia decyzję. W niektórych przypadkach, aby znaleźć wartość nieznanych, wskazane jest, aby zastosować grafiki.
Article in other languages:
AR: https://tostpost.com/ar/education/15212-irrational-equations-and-their-solutions.html
BE: https://tostpost.com/be/adukacyya/26336-racyyanal-nyya-ra-nenn-sposaby-h-vyrashennya.html
DE: https://tostpost.com/de/bildung/26008-gleichungen-irrationale-und-deren-l-sungen.html
En: https://tostpost.com/education/25951-irrational-equations-and-their-solutions.html
ES: https://tostpost.com/es/la-educaci-n/25909-ecuaciones-irracionales-y-sus-soluciones.html
HI: https://tostpost.com/hi/education/14969-irrational-equations-and-their-solutions.html
JA: https://tostpost.com/ja/education/14925-irrational-equations-and-their-solutions.html
KK: https://tostpost.com/kk/b-l-m/26603-irracional-te-deuler-zh-ne-olardy-sheshu-t-s-lder.html
PT: https://tostpost.com/pt/educa-o/27394-equa-o-irracional-e-suas-solu-es.html
TR: https://tostpost.com/tr/e-itim/26540-denklemler-mant-ks-z-ve-z-mleri.html
UK: https://tostpost.com/uk/osv-ta/26884-rrac-onal-n-r-vnyannya-ta-sposobi-h-vir-shennya.html
ZH: https://tostpost.com/zh/education/5874-irrational-equations-and-their-solutions.html

Alin Trodden - autor artykułu, redaktor
"Cześć, jestem Alin Trodden. Piszę teksty, czytam książki, Szukam wrażeń. I nie jestem zły w opowiadaniu ci o tym. Zawsze chętnie biorę udział w ciekawych projektach."
Nowości
Jak się nazywa Einsteina? Kim Einstein?
Geniusz słynnego fizyka-teoretyka A. Einsteina zapewniła mu światową sławę już za życia. Sześćdziesiąt lat po jego śmierci, świat nadal zachwyca głębią teorii i odwagą założeń naukowca.Jednak coraz częściej można usłyszeć pytanie ...
Podział komórek: opis głównych procesów
Podział komórek ó jest to naturalny proces, który zapewnia prawidłowy wzrost, rozwój i rozmnażanie organizmu. Dzięki temu zwiększa się liczba komórek, następuje wzrost tkanek, rozmnażanie płciowe i wysyłanie dziedzicznego m...
polska w 17 wieku, osłabiony wewnętrznym kryzysem społecznym i polsko-szwedzkiej interwencją, musiała pogodzić się ze swoimi terytorialne straty: Яи, Копорье, Ивангород, a także Smoleńsk, черниговские ziemi odeszli do jej sąsiadów...
Zintegrowane zajęcia z dziećmi w wieku przedszkolnym
Federalnymi i krajowymi przepisami (ФГТ) programie edukacyjnym, realizowanych w przedszkolu, polecana jest organizacja i prowadzenie z dziećmi różnych rodzajów działalności, w trakcie których mogą być realizowane cele edukacyjne: ...
Несклоняемые rzeczowniki: rodzaje, zasady ustalania ich rodzaju, przykłady.
Spadek - to zmiana na liczby i liczby rzeczowników. Istnieją trzy typy deklinacji. Oprócz tego istnieją разносклоняемые (dziesięć rzeczowników por. rodzaju, które kończą się na-mja, a także słowa córka, droga, matka, dziecko) i не...
Historia rodziny Warren: prawdziwi pogromcy duchów
Ed i Lorraine Уоррены ó jedne z najbardziej znanych badaczy zjawisk paranormalnych. W ciągu dziesięcioleci ta para разъезжала w kraju, przychodzi na pomoc ludziom cierpiącym nadprzyrodzonej aktywności. Ale jaka jest właściw...






















Uwaga (0)
Ten artykuł nie ma komentarzy, bądź pierwszy!