Now - 22:02:36
Ecuaciones irracionales y sus soluciones
Estudiar el álgebra, los estudiantes se enfrentan con las ecuaciones de muchas especies. Entre aquellos que son más simples, se puede llamar lineales que contienen una desconocida. Si la variable en notación matemática se está construyendo en cierto grado, la ecuación se llama cuadrada, cúbica, биквадратным y así sucesivamente. Estos expresiones pueden contener números racionales. Pero también existen ecuaciones irracionales. De otros que difieren en función de donde lo desconocido se encuentra bajo el signo radical (es decir, puramente exteriormente la variable aquí se puede ver escrito por debajo de la raíz cuadrada). Solución de ecuaciones exponenciales tiene sus rasgos característicos. Al calcular el valor de la variable para obtener la respuesta correcta debe tener necesariamente en cuenta.

Indecibles palabras»
No es un secreto que los antiguos matemáticas son principalmente a números racionales. Se trata, como se sabe, enteras, expresadas a través de acciones ordinarias y decimales periódicos fracciones representantes de esta comunidad. Sin embargo, los científicos de Medio oriente, así como de la india, el desarrollo de la trigonometría, la astronomía y el álgebra, ecuaciones irracionales también aprendieron a resolver. Por ejemplo, los griegos sabían similares en magnitud, pero, elevando en forma verbal, empleaban el concepto de «алогос», que significa indecibles». Más tarde, los europeos, imitando lo que se llamaban similares en el número de la sordos». De todos los demás pero se diferencian en que sólo pueden ser representados en forma de infinito непериодической de la fracción final de una expresión numérica que conseguir es simplemente imposible. Por lo tanto, a menudo similares a los representantes del reino de los números se escriben como números y caracteres como cierta la expresión que está debajo de la raíz de segundo o mayor grado.
Más:
El general walter von Reichenau: su biografía, sus logros y la historia
El General mariscal de campo de la alemania nazi walter von Reichenau (Walter von Reichenau) se contaba entre los pocos altos oficiales del ejército de la wehrmacht, que apoyó activamente el nazismo. Durante la Segunda guerra mundial fue comandante d...
Trajes espaciales de los astronautas: de la asignación de la unidad. El primer traje espacial
Trajes espaciales de los astronautas – no es simplemente trajes de vuelo en órbita. El primero de ellos se remonta a principios del siglo veinte. Era la época de antes de los vuelos espaciales restaba casi medio siglo. Sin embargo, los científi...
Oriental de la plataforma europea: forma de alivio. Minerales oriental de la plataforma europea
La Mayor parte del territorio europeo de rusia, así como de algunos países de la cei se encuentra en la parte continental de un tramo de la corteza terrestre, que lleva el nombre oriental de la plataforma europea. La forma del relieve aquí es predomi...
En la base de lo anterior, intentaremos dar una definición de la ecuación irracional. Tales expresiones contienen los llamados indecibles número», grabados con el uso del signo de la raíz cuadrada. Ellos pueden ser una variedad muy complejos, pero en su наипростейшей formulario son de este tipo, como en la foto de abajo.
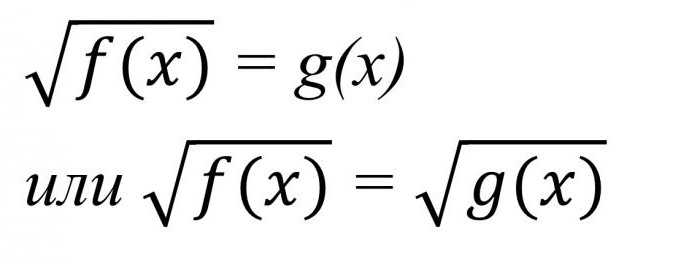
Faltas contra de la decisión de ecuaciones exponenciales, lo primero es lo primero, se debe calcular el margen de tolerancia de la variable.
¿qué sentido Tiene la expresión?
La Necesidad de revisar los valores se deriva de las propiedades de la aritmética del cuadrado de la raíz. Como se sabe, similar a la expresión aceptable y tiene algún sentido sólo en ciertas condiciones. En los casos de la raíz par la medida de todas las подкоренные de expresión deben ser positivos o cero. Si esta condición no se cumple, en este matemático de la escritura no puede considerarse significativa.
Damos un ejemplo concreto de cómo resolver ecuaciones irracionales (en la foto de abajo).
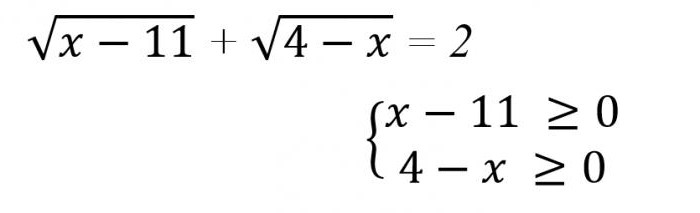
En este caso es evidente que las condiciones especificadas en ningún de los valores, adoptadas por la magnitud, no se puede realizar ninguna, porque resulta que el 11 ≤ x ≤ 4. Entonces, la solución puede ser sólo Ø.
El Método de análisis
A Partir de lo anterior queda claro cómo resolver los irracionales de la ecuación de algunos de los tipos. Aquí eficaz puede ser un simple análisis.
Presentan una serie de ejemplos, que de nuevo de un modo evidente lo demuestran (en la foto de abajo).
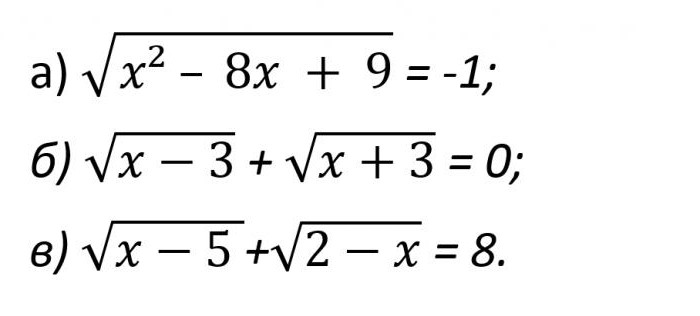
En el primer caso, un examen detallado de la expresión se ve muy claro que el verdadero que no puede ser. Realmente, ya que en la parte izquierda de la igualdad debe resultar un número positivo, que no puede ser igual a -1.
En el segundo caso, la suma de las dos expresiones positivas puede considerarse igual a cero, cuando x - 3 = 0 y x + 3 = 0 a la vez. Y similar de nuevo es imposible. Y entonces, en la respuesta de nuevo debe escribir Ø.
El Tercer ejemplo es muy similar al ya descrito anteriormente. Realmente, ya que aquí las condiciones de salud requieren que se realice la siguiente absurdo de la desigualdad: 5 ≤ x ≤ 2. Y similar a la ecuación de igual manera no puede tener sólidas de decisiones.
Ilimitado aproximación
La Naturaleza irracional de la más clara y completa puede ser explicada por el y conocida sólo a través de una serie infinita de números decimales. Y específicos, un claro ejemplo de los miembros de esta familia es πes decir, No sin razón, se supone que esta una constante matemática ha sido conocida desde la antigüedad, acostumbrado al calcular las longitudes de la circunferencia y área del círculo. Pero entre los europeos por primera vez poner en práctica el inglés william jones y el suizo leonard euler.

Se Produce esta constante de la siguiente manera. Si se compara una variedad de la longitud de la circunferencia, de la actitud de sus longitudes y diámetros obligatoriamente igual a uno y el mismo número. Es πes decir, Si expresar a través de la fracción ordinaria, aproximadamente recibimos 22/7. Por primera vez hizo un gran arquímedes, el retrato que presenta la ilustración de arriba. Es por eso que una cantidad similar de recibió su nombre. Pero no es explícita, y un valor aproximado casi más sorprendente de los números. Un brillante científico con una precisión de hasta 0,02 encontrado lo que busca la cantidad, perohecho, esta constante no tiene valor real, y se expresa como 3,1415926535… es una serie infinita de números, indefinidamente acercándose a un мифическому valor.
La Erección en el cuadrado
Pero volvamos a la irracional a las ecuaciones. Con el fin de encontrar lo desconocido, en este caso, muy a menudo recurren a un simple método: elevan ambos lados de la parte disponible de la igualdad en el cuadrado. Este método suele dar buenos resultados. Pero debe tenerse en cuenta de la astucia de las magnitudes irracionales. Todas las resultantes de las raíces, se debe comprobar, ya que pueden no ser apropiados.
Pero continuaremos el examen de los ejemplos y tratar de encontrar las variables de nuevo recomendada.
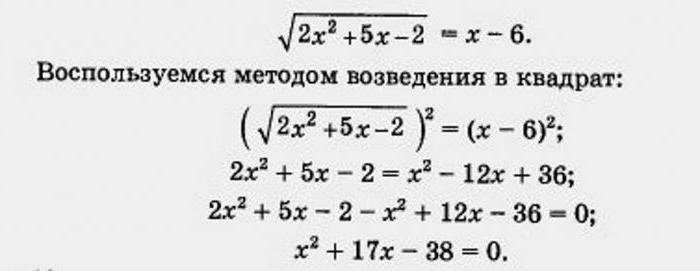
Es Muy fácil, aplicando el teorema de Виета, encontrar los valores de las magnitudes después, como resultado de ciertos оперций el de nosotros se ha formado ecuación cuadrática. De aquí resulta que entre las raíces serán el 2 y el 19. Sin embargo, al comprobar, sustituyendo recibidos el valor original de la expresión, puede asegurarse de que ninguna de estas raíces no es válido. Es frecuente en ecuaciones irracionales. Por lo tanto, nuestra dilema de nuevo no tiene soluciones, y en la respuesta se debe especificar un conjunto vacío.
Ejemplos de посложней
En algunos casos, es necesario elevar al cuadrado ambos lados de la parte de la expresión no una, sino varias veces. Veamos algunos ejemplos donde se requiere especificado. Se puede ver a continuación.
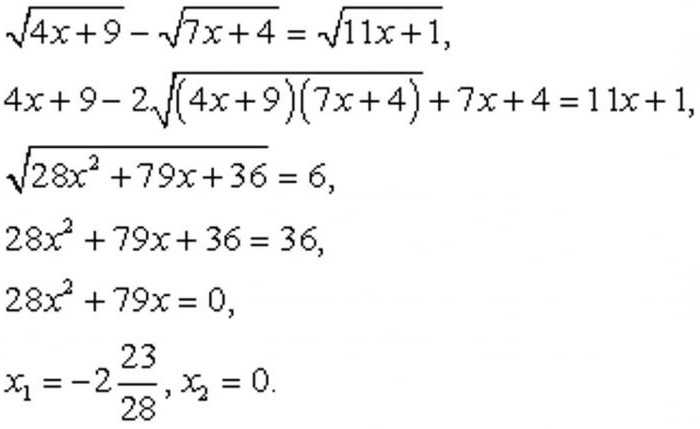
Después de Recibir las raíces, no nos olvidamos de sus comprobar, ya que pueden producirse excedentes. Debe explicar por qué esto es posible. Al aplicar este método se produce, en cierto modo, la racionalización de la ecuación. Pero olvidar no deseados nos raíces que impiden producir las operaciones aritméticas, se les extendemos la existente en el área de valores, lo que podría ser (como se puede deducir consecuencias. Previendo esto, nos hacemos la comprobación. En este caso, tiene la oportunidad de asegurarse de que es adecuado sólo una de las raíces: x = 0.
Sistema
¿Qué hacer en los casos en que es necesario realizar la solución de sistemas de ecuaciones exponenciales, y disponemos de no uno, sino dos desconocidos? Aquí hacemos lo mismo, como en los casos normales, pero teniendo en cuenta las anteriores propiedades de los datos de las expresiones matemáticas. Y en cada nueva tarea, por supuesto, se debe aplicar la creatividad. Pero, de nuevo, es mejor considerar todo un ejemplo concreto, presentado a continuación. Aquí no sólo se requiere encontrar las variables x e y, pero y especificar en la respuesta la suma de sus. Así, dispone de un sistema que contiene irracionales de magnitud (ver foto abajo).

Como puede ver, esta tarea no es nada sobrenatural complejo. Solo se requiere demostrar la inteligencia y la conjetura de que la parte izquierda de la primera ecuación representa el cuadrado de la suma. Estas tareas se encuentran en uso.
Irracional en matemáticas
Cada vez que la necesidad de la creación de nuevos tipos de números ocurría con el de la humanidad, cuando no tenía la espacio» para la solución de cualquier tipo de ecuaciones. Irracionales los números no son la excepción. Como demuestran los hechos de la historia, por primera vez, los grandes sabios han prestado atención a esto antes de nuestra era, en el siglo VII. Lo hizo el matemático de la india, conocido bajo el nombre de Манава. Él comprendía claramente que algunas de números naturales no es posible extraer la raíz. Por ejemplo, se trata de 2; 17 y 61, así como muchos otros.
Uno de los pitagóricos, el pensador de nombre Гиппас, llegó a la misma conclusión, tratando de hacer cálculos con expresiones numéricas de las partes en el pentagrama. Abriendo matemáticos de los elementos que no se pueden expresar valores numéricos y no poseen las propiedades normales de números, es tan разозлил de sus colegas, que fue arrojado por la borda de la nave en el mar. El hecho de que otros пифагорейцы consideraron su razonamiento en la rebelión contra las leyes del universo.
El Signo radical: la evolución de la
El Signo de la raíz para expresar el valor numérico de la sordos» números comenzó a usarse el caso de una decisión irracional de las desigualdades y ecuaciones no de inmediato. Por primera vez acerca de радикале comenzaron a pensar europeos, especialmente italianos, de las matemáticas, aproximadamente en el siglo XIII. Entonces, para designar inventado utilizar latina de R. Pero alemanas de las matemáticas en sus trabajos, no lo hicieron. Les gustó la letra V. En alemania, pronto se extendió la designación de la V(2), V(3), lo que se pretende es expresar la raíz cuadrada de 2, 3 y así sucesivamente. Más tarde en el caso intervino ¡ellos y видоизменили el signo del radical. Y completó la evolución de rené descartes, elevando el signo de la raíz cuadrada y contemporáneo de la perfección.

La Liberación de lo irracional
Irracionales de ecuaciones y desigualdades pueden incluir la variable no sólo bajo el signo de la raíz cuadrada. Puede ser de cualquier grado. La forma más común de deshacerse de él es la posibilidad de construir las dos partes de la igualdad en distinto grado. Esta es la principal acción que ayuda a las operaciones con la irracional. Pasos en pares casos, especialmente no difieren de aquellos que han sido ya analizado por nosotros anteriormente. Aquí se deben tener en cuenta las condiciones de неотрицательности подкоренного de expresión, así como al final de la decisión, debe producir el abandono extraños de valoreslas variables de esta manera, como se muestra en los ejemplos ya.
De las conversiones adicionales que ayudan a encontrar la respuesta correcta, a menudo se utiliza la multiplicación de expresiones en el empleo y, a menudo, requiere la introducción de una nueva variable, lo que facilita la decisión. En algunos casos, con el fin de encontrar el valor desconocido, es aconsejable aplicar gráficos.
Article in other languages:
AR: https://tostpost.com/ar/education/15212-irrational-equations-and-their-solutions.html
BE: https://tostpost.com/be/adukacyya/26336-racyyanal-nyya-ra-nenn-sposaby-h-vyrashennya.html
DE: https://tostpost.com/de/bildung/26008-gleichungen-irrationale-und-deren-l-sungen.html
En: https://tostpost.com/education/25951-irrational-equations-and-their-solutions.html
HI: https://tostpost.com/hi/education/14969-irrational-equations-and-their-solutions.html
JA: https://tostpost.com/ja/education/14925-irrational-equations-and-their-solutions.html
KK: https://tostpost.com/kk/b-l-m/26603-irracional-te-deuler-zh-ne-olardy-sheshu-t-s-lder.html
PL: https://tostpost.com/pl/edukacja/27666-r-wnania-irracjonalne-i-sposoby-ich-rozwi-zania.html
PT: https://tostpost.com/pt/educa-o/27394-equa-o-irracional-e-suas-solu-es.html
TR: https://tostpost.com/tr/e-itim/26540-denklemler-mant-ks-z-ve-z-mleri.html
UK: https://tostpost.com/uk/osv-ta/26884-rrac-onal-n-r-vnyannya-ta-sposobi-h-vir-shennya.html
ZH: https://tostpost.com/zh/education/5874-irrational-equations-and-their-solutions.html

Alin Trodden - autor del artículo, editor
"Hola, soy Alin Trodden. Escribo textos, leo libros y busco impresiones. Y no soy mala para decírtelo. Siempre estoy feliz de participar en proyectos interesantes."
Noticias Relacionadas Con La
la Sociedad y su estructura – uno de los problemas centrales en la sociología. Algunos tutoriales incluso lo definen como objeto de la ciencia. Cualquier sociedad – no es un monolito, no es algo homogéneo. ...
Estilos de voz es históricamente consagrados en el lenguaje de formas del discurso, propias de los diferentes tipos de comunicación. Cada estilo se caracteriza por su conjunto de características de habla, es adecuado en un ámbito ...
La teoría, las ideas y los principios de la escuela neoclásica
la escuela Neoclásica – esta dirección, formado en el ámbito económico, su primera aparición fue en los años noventa. A desarrollarse durante el inicio de la segunda fase de la маржиналистской de la revolución, y esto está r...
Asígnele el planeta más cercano al Sol!
elige el más cercano al planeta al Sol! Y la mayor planeta de nuestro sistema? Y cuántos de ellos, en realidad? No todo el mundo inmediatamente se acordará de las respuestas a estas preguntas. Aún más, se sorprenderá de aquellos q...
La sociedad feudal. Los estamentos de la sociedad feudal
la sociedad Feudal se consideraba prácticamente universal de la forma de control de eurasia. La mayoría de los pueblos que habitaban su pasado a través de este sistema. A continuación, consideremos más que un representó a la socie...
La hazaña de víctor Талалихина - breve
En la parte central de la ciudad de Вольска, cerca del mercado, vale la pena humilde de madera pequeña casita, qué mucho por aquí. En él vive la gente, pero en la pared de fijada la placa de inserción de los transeúntes acerca de ...





















Comentarios (0)
Este artículo no tiene comentarios, se el primero!