Now - 07:52:41
مشاكل غير قابلة للحل: Navier -- يذكي المعادلات ، هودج التخمين ، فرضية ريمان. أهداف الألفية
مهمة مستحيلة 7 الأكثر إثارة المشاكل الرياضية. كل واحد منهم كان المقترحة من قبل مشاهير العلماء, كقاعدة عامة, في شكل فرضيات. لعقود عديدة ، على قرار كسر رأس الرياضيات في العالم. أولئك الذين ينجحون ، تكافأ مع ملايين الدولارات التي يقدمها المعهد Claa.
ما قبل التاريخ
في عام 1900 العظيم عالم الرياضيات الألماني العالمي ديفيد هيلبرت قدمت قائمة من 23 المشاكل.
الدراسات التي أجريت بهدف حل لهم ، كان له تأثير هائل على العلم القرن 20th. في هذه اللحظة الأكثر منهم قد توقفت عن أن تكون الألغاز. بين العالقة أو جزئيا حلها هو اليسار:
- مشكلة تناسق الحسابيه البديهيات ؛
- قانون عام المعاملة بالمثل في الفضاء من أي العددية الميدان ؛
- دراسة رياضية المادية البديهيات ؛
- دراسة اشكال من الدرجة الثانية مع التعسفي جبري عدد معاملات;
- المشكلة بدقة escalerillas الهندسة فيدور شوبرت ؛
- إلخ.
غير مستكشفة: مشكلة التوزيع في أي جبري مجال العقلانية المعروفة نظرية كرونيكير فرضية ريمان.
معهد Kleya
تحت عنوان الشهيرة خاصة غير ربحية المنظمة التي يقع مقرها الرئيسي في كامبريدج بولاية ماساتشوستس. وقد تأسست في عام 1998 من قبل جامعة هارفارد رياضيات A. جافي و رجل الأعمال L. المطالبة. الهدف من المعهد هو تعزيز وتطوير المعرفة الرياضية. لتحقيق هذه المنظمة يعطي جوائز العلماء و المقدمين بحثية واعدة.
المزيد
أساليب التدريس التفاعلية في جامعة
أساليب التدريس التفاعلية هي واحدة من أهم وسائل تحسين التدريب المهني من الطلاب في التعليم العالي. المعلم هو الآن لا يكفي أن تكون ببساطة المختصة في الانضباط ، وإعطاء المعرفة النظرية في الفصول الدراسية. تحتاج بعض نهج مختلف الحديثة في العملية التعليمية.ن...
البرازيل الذي أعداد السكان في المرتبة الخامسة المرتبة الثانية بعد الهند والصين وإندونيسيا وأمريكا – متنوعة جدا البلد. لعدة مئات من السنين الأمة أصبح من أهم العرقية-الثقافية والتعليم. سكان البرازيل هو أكثر من مائة القوميات والشعوب. في هذا ...
مستعمرة من بريطانيا – العديد من المناطق في جميع أنحاء العالم ، الذين تم القبض عليهم ، تؤخذ تحت الحماية أو بعض الوسائل المكتسبة بين 16 و 18 قرون واحدة من أقوى الإمبراطوريات في الماضي – البريطانية. وكان الهدف من التنمية الإقليمية. خلال الفت...
في أوائل القرن ال21 Cleia الرياضية المعهد تقديم جائزة لمن يحل المشكلة ، الذي يعرف باسم الأكثر تعقيدا مشاكل غير قابلة للحل ، داعيا قائمة الألفية جائزة المشاكل. من “قائمة جيلبرت” فإنه يشمل فقط فرضية ريمان.
الأهداف
في قائمة معهد Klaa شمل في البداية:
- الفرضية على هودج دورات ؛
- معادلات نظرية الكم يانغ ميلز;
- بوانكاريه ؛
- مشكلة المساواة بين الطبقات P و NP ؛
- فرضية ريمان;
- Navier -- يذكي المعادلات وجود ونعومة قراراته ؛
- مشكلة البتولا Swinnerton-داير.
هذه المشاكل الرياضية ذات أهمية كبيرة, نظرا لأنها يمكن أن يكون لها العديد من التطبيقات العملية.
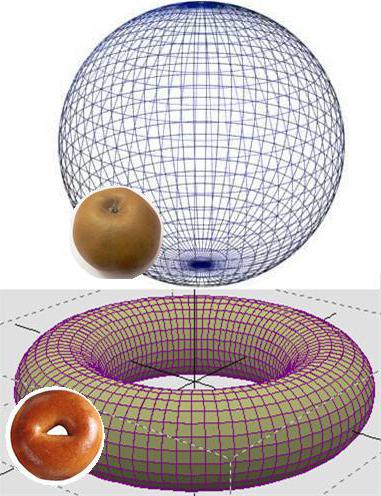
ثبت من قبل غريغوري بيرلمان
في عام 1900 ، الشهير الفيلسوف هنري بوانكاريه اقترح أن كل اتصال بكل بساطة المدمجة 3-الأبعاد المتعددة دون حافة homeomorphic 3-الأبعاد المجال. الاثبات في قضية عامة ليس عن قرن. فقط في الفترة 2002-2003 ، سانت بطرسبرغ رياضيات G. بيرلمان نشرت سلسلة من المقالات حل بوانكاريه المشكلة. أنها تنتج قنبلة. في عام 2010 ، بوانكاريه تم استبعاده من قائمة “التحديات" معهد Kleya معظم بيرلمان دعي إلى نتيجة له جائزة كبيرة ، الذي رفض هذا الأخير ، دون أن يوضح أسباب قراره.
الأكثر تفسيرا واضحا ما لم يثبت الروسية الرياضيات ، يمكن أن تعطي, تخيل ماذا الخبز (الحيد), سحب المطاط القرص ثم محاولة سحب حافة محيط به عند نقطة واحدة. ومن الواضح أن هذا مستحيل. شيء آخر, إذا قمت بإجراء هذه التجربة مع العالم. في هذه الحالة, يبدو أن المجال ثلاثي الأبعاد التي تم الحصول عليها من القرص محيط والتي يتم سحبها إلى نقطة افتراضية سلك ثلاثي الأبعاد في فهم الشخص العادي ، ولكن ثنائي الأبعاد من وجهة نظر الرياضيات.
پوانكاريه اقترح هذا المجال ثلاثي الأبعاد هو فقط ثلاثي الأبعاد “موضوع" السطحية التي يمكن أن تقلص إلى نقطة واحدة ، بيرلمان كان قادرا على إثبات ذلك. وهكذا ، فإن قائمة من “غير قابلة للحل” اليوم يتكون من 6 مشاكل.

يانغ ميلز
هذه مشكلة الرياضيات المقترح من قبل مؤلفيه في عام 1954 م إلى سنة. العلمي صياغة نظرية النموذج التالي: لأي بسيطة مدمجة قياس مجموعة من الكم المكانية النظرية التي أنشأتها يانغ Millsom موجودة صفر كتلة عيب.
إذا كنت تتحدث لغة غير مفهومة للشخص العادي ، التفاعل بين الكائنات الطبيعية (الجسيمات, الهيئات, موجات, الخ.) تنقسم إلى 4 أنواع: الكهرومغناطيسية الجاذبية الضعيفة و القوية. لسنوات عديدة علماء الفيزياء يحاولون إنشاء العامة نظرية الحقل. ينبغي أن يكون أداة لحساب كل هذه التفاعلات. نظرية يانغ ميلز هو اللغة الرياضية التي تصف 3 من 4 من القوى الأساسية في الطبيعة. فإنه لا ينطبق على الجاذبية. ولذلك لا يمكن افتراض أن يانغ ميلز قادرة على خلق نظرية المجال.
وبالإضافة إلى ذلك ، فإن المقترح غير خطية من المعادلات يجعلها من الصعب جدا حل. الصغيرة الثوابت عندما يمكن تقريبا يمكن حلها في شكل اضطراب سلسلة. ومع ذلك ، فمن غير الواضح كيف يمكن حل هذه المعادلات في اتصال قوية.

Navier -- يذكي المعادلات
استخدام هذه التعابير لوصف العمليات مثل تدفق الهواء ، للسوائل و الاضطراب. في بعض الحالات الخاصةالحلول التحليلية من Navier -- يذكي المعادلات تم العثور عليها ، ولكن للقيام بذلك المشتركة حتى الآن لا أحد لديه. في نفس الوقت, محاكاة عددية محددة قيم السرعة والكثافة والضغط الوقت حتى يسمح لنا لتحقيق نتائج ممتازة. ومن المؤمل أن شخص ما سوف تكون قادرة على تطبيق Navier -- يذكي المعادلات في الاتجاه المعاكس ، أي لحساب المعلمات ، أو أن يثبت أن هذه الطريقة لا يوجد حل.
مهمة البتولا Swinnerton-داير
فئة “التحديات” يشير إلى الفرضية التي اقترحها الإنجليزية علماء من جامعة كامبريدج. 2300 سنة قبل الباحث اليوناني القديم اقليدس أعطى وصفا كاملا حلول المعادلة x2 + y2 = z2.
إذا كان لكل من يعبي هو لحساب عدد من النقاط على منحنى في وحدة ، يمكنك الحصول على مجموعة لانهائية من الاعداد الصحيحه. إذا طريقة معينة “الغراء” في 1 وظيفة معقدة ومتغيرة ، ثم الحصول على زيتا وظيفة هاس-حسنا بالنسبة مكعب منحنى ، ويرمز له بالحرف L. أنه يحتوي على معلومات حول سلوك مودولو كل يعبي في آن واحد.
براين البتولا بيتر Swinnerton-داير وقد طرحت فرضية بخصوص المنحنيات الاهليلجيه. وفقا لها, هيكل وعدد من العديد من الحلول العقلانية المرتبطة سلوك L-وظائف في الوحدة. مثبتة في هذه اللحظة ، فرضية البتولا Swinnerton-داير يعتمد على وصف المعادلات الجبرية من الدرجة 3 و هو الوحيد بسيطة نسبيا الطريقة العامة لحساب رتبة المنحنيات الاهليلجيه.
فهم أهمية عملية من هذه المهمة ، ويكفي أن نقول أن في التشفير الحديثة على أساس المنحنيات الاهليلجيه فئة كاملة من غير المتكافئة ونظم استخدام المعايير المحلية القائمة على التوقيعات الرقمية.

ف مقابل np
إذا كان ما تبقى من "أهداف الألفية" تنتمي إلى رياضي بحت, ثم وهذا هو ذات الصلة إلى نظرية الخوارزميات. مسألة المساواة بين الطبقات p و np, المعروف أيضا باسم مشكلة طبخ-ليفين و لغة بسيطة يمكن أن تصاغ على النحو التالي. أعتقد أن إجابة إيجابية على سؤال يمكن التحقق بسرعة ، أي في وقت متعدد الحدود (PV). ثم أنه من الصحيح أن نؤكد أن الإجابة يمكن أن تكون سريعة جدا أن تجد ؟ حتى أسهل هذه المهمة يبدو ذلك: ما إذا كان حقا حل مشكلة الاختبار ليس أكثر صعوبة من العثور عليه ؟ إن المساواة بين الطبقات p و np سوف يكون من أي وقت مضى ثبت ، ثم جميع مشاكل اختيار يمكن حلها الكهروضوئية. في هذه اللحظة العديد من المتخصصين في شك من صحة هذا البيان ، على الرغم من أنني لا يمكن أن يثبت خلاف ذلك.

فرضية ريمان
حتى عام 1859 كان هناك لم يتم الكشف عن أي النظم التي تصف كيف الأعداد الأولية تتوزع بين الطبيعية. ربما كان ذلك راجعا إلى حقيقة أن العلم كانت تعمل في المسائل الأخرى. ولكن بحلول منتصف القرن 19 الحالة تغيرت و أصبحت واحدة من أكثر ذات الصلة ، والتي بدأت في الانخراط في الرياضيات.
فرضية ريمان ظهرت في هذه الفترة هو افتراض أن توزيع الأعداد الأولية هناك نمط واضح.
اليوم كثير من علماء الحديث نعتقد أنه إذا ثبت علينا إعادة النظر في العديد من المبادئ الأساسية من التشفير الحديثة ، العمود الفقري جزء كبير من التجارة الإلكترونية.
ووفقا فرضية ريمان طبيعة توزيع الأعداد الأولية ، ربما يختلف كثيرا عن المقصود في هذه اللحظة. والحقيقة هي أنه حتى الآن لم يتم اكتشاف أي نظام في توزيع الأعداد الأولية. على سبيل المثال ، هناك مشكلة ‘التوائم", الفرق بين الذي يساوي 2. هذه الأرقام هي 11 و 13 ، 29. غيرها من الأعداد شكل مجموعات. هذا 101, 103, 107, الخ ، العلماء يشتبهون منذ فترة طويلة أن هذه المجموعات موجودة بين مجموعة كبيرة جدا يعبي. إذا كنت تجد لهم متانة الحديثة مفاتيح التشفير ستكون موضع شك.

الفرضية على هودج دورات
هذا لا تزال دون حل المشكلة التي صيغت في عام 1941. على هودج التخمين يشير إلى إمكانية تقارب شكل أي كائن من قبل "الإلتصاق" معا بسيطة الهيئات من أعلى الأبعاد. وكانت هذه الطريقة معروفة و استخدمت بنجاح لفترة طويلة. ولكن من غير المعروف إلى أي مدى من الممكن أن تجعل التبسيط.
الآن أنت تعرف ماذا مشاكل غير قابلة للحل توجد في الوقت الراهن. فهي موضوع البحث الآلاف من العلماء في جميع أنحاء العالم. ومن المؤمل أن يتم في المستقبل القريب سوف يتم حلها ، وتطبيقها بصورة عملية من شأنها المساعدة الإنسانية إلى مرحلة جديدة من التطور التكنولوجي.
Article in other languages:
HI: https://tostpost.com/hi/education/1204-navier--riemann.html
JA: https://tostpost.com/ja/education/1203-navier-stokes-hodge.html

Alin Trodden - مؤلف المقال ، محرر
"مرحبا ، أنا ألين الدوس. أنا أكتب النصوص ، وقراءة الكتب ، والبحث عن الانطباعات. وأنا لست سيئة في أقول لك عن ذلك. أنا دائما سعيد للمشاركة في مشاريع مثيرة للاهتمام."
أخبار ذات صلة
المعمارية جامعات روسيا: تصنيف وصف الميزات استعراض
تطوير المخططات الهندسية والرسومات تنفيذ متكلفا مشاريع البناء ، واستكمال إنشاء كائن وتسليمه إلى العميل – جميع هذا المجال من النشاط المهني للمهندسين المعماريين. في هذه المادة ونحن سوف قائمة المعروفة والأكثر شعبية بين الطلاب ال...
البيض هو الخلايا التناسلية للإناث ، الذي يحتوي على فرداني مجموعة من الكروموسومات. الغرض الأساسي نقل المعلومات الوراثية أثناء الإخصاب. هيكل البيض في الطبيعة يمكن أن تكون متنوعة جدا. على سبيل المثال, البيضة هو بطارخ ال...
العقارات-ممثل الملكي شكل الحكومة ،
النظام الملكي هو من بين أقدم أشكال الحكومة. خصوصية تكمن في حقيقة أن السلطات على كل مجالات الدولة ينتمي إلى شخص واحد من حق الخلافة. في العصور القديمة كان يعتقد أن خادم الحرمين الشريفين – الممسوح من الله. ومع ذلك ، في كثير من ...
تحليل الأنشطة الاقتصادية – وهو نظام من التقنيات المتقدمة من خلال المنهج العلمي ، وذلك بسبب والتي يصبح من الممكن دراسة الاقتصاد. مع استخدامه في تحديد الإنتاج والاحتياطيات وفقا المحاسبة المحاسبة والمعلومات المتقدمة أكثر الطرق ...
لحظة من الجمود. بعض التفاصيل من ميكانيكا المواد الصلبة
واحدة من المبادئ الأساسية المادية من التفاعل بين الأجسام الصلبة هو قانون القصور الذاتي ، التي صاغها العظيم إسحاق نيوتن. بهذا المفهوم نحن نواجه باستمرار تقريبا ، كما أن لديها تأثير كبير جدا على جميع الأشياء المادية من العالم ، بما ...
1147 - ما هو سن لتطوير موسكو ؟
“آلهة من القياصرة الروس" يحتوي على المعلومات التي أول القبائل في إقليم موسكو الحديثة يتقن هذه الأراضي في 880 السنة. كثير من العلماء يتساءلون: 1147 - ما هو سن تشكيل الدولة الروسية? موسكو-نهر في تلك الأيام كان يطلق عليه ا...






















تعليقات (0)
هذه المادة قد لا تعليق أول