Now - 19:39:12
Zawiłe zadania: równania Naviera-Stokesa, hipoteza Hodge ' a, hipoteza Riemanna. Zadania tysiąclecia
Zawiłe zadania ó 7 ciekawych problemów matematycznych. Każda z nich była oferowana w swoim czasie znanymi naukowcami, zwykle w postaci hipotez. Od wielu już lat nad ich rozwiązaniem łamią sobie głowy matematyki na całym świecie. Każdego, kto osiągnie sukces, czeka nagroda w wysokości miliona dolarów amerykańskich, proponowane przez instytut Клэйя.
Historia
W 1900 roku, wielki matematyk niemiecki-kombi David Hilbert przedstawił listę 23-tych problemów.
Badania, zrealizowane w celu ich rozwiązania, wywarły ogromny wpływ na naukę 20 wieku. W tej chwili większość z nich już przestały być zagadkami. W tym nierozwiązanych lub rozwiązanych częściowo pozostały:
- Problem spójność aksjomatów arytmetycznych;
- Ogólne prawo wzajemności na przestrzeni dowolnego pola liczbowego;
- Matematyczne badanie fizycznych aksjomatów;
- Badanie kwadratowe formy w dowolnych liczb algebraicznych współczynnikach;
- Problem ścisłego uzasadnienia исчислительной geometrii Fedor Schuberta;
- Itp.
Niezbadane są: problem dystrybucji na dowolny алгебраическую obszar racjonalności znanego twierdzenia Кронекера i hipoteza Riemanna.
Instytut Клэйя
Pod tą nazwą znana jest prywatna organizacja non-profit, której siedziba znajduje się w Cambridge, w stanie Massachusetts. Została założona w 1998 roku przez harvard matematyka A. Джеффи i biznesmenem Moc Клэйем. Celem działalności instytutu jest popularyzacja i rozwój wiedzy matematycznej. Aby go osiągnąć organizacja wyda nagrody naukowcom i sponsoruje obiecujące badania.
Bardziej:
Główne etapy rozwoju psychiki w филогенезе
Rozwój psychiki w филогенезе charakteryzuje się kilkoma etapami. Rozważmy dwie główne historie związane z tym procesem.Филогенез - to historyczny rozwój, obejmującego miliony lat ewolucji, historię rozwoju różnych gatunków organizmów żywych.Ontogenez...
Co to jest gronkowiec i metody jego leczenia
Wielu w swoim życiu miał do czynienia z zakażeniem gronkowca. Dlatego konieczne jest posiadanie pełnej informacji o tej chorobie, aby w pełni zrozumieć, co dzieje się w organizmie. Więc co to jest gronkowiec? To bakterie, lub jedną z ich odmian, z kt...
Przed podjęciem się, że studiuje morfologia, należy zauważyć, że sam studiuje ten dział gramatyki. Tak, morfologia studiuje słowo jako część mowy, a także sposoby jego edukacji, jego formy, struktury i gramatyki wartości, a także poszczególne j...
Na początku 21 wieku, instytut Matematyczny Клэйя zaproponował nagrodę tym, którzy rozwiąże problemy, które są znane, jako najbardziej skomplikowane zadania zawiłe, nazywając swoją listę Millennium Prize Problems. Z «Listy Huberta» w niego weszła tylko hipoteza Riemanna.
Zadania millenium
Na listę instytutu Клэйя początkowo wchodziły:
- Hipoteza o cyklach Hodge 'a;
- Równań kwantowej teorii Younga ó Mills' a;
- Hipoteza Poincare;
- Problem równości klasy P i NP;
- Hipoteza Riemanna;
- Równania Naviera Stokesa, o istnieniu i gładkość jego decyzji;
- Problem Берча ó Свиннертон-Farbiarski.
Te otwarte matematyczne problemy są ogromne zainteresowanie, ponieważ mogą mieć wiele praktycznych wdrożeń.
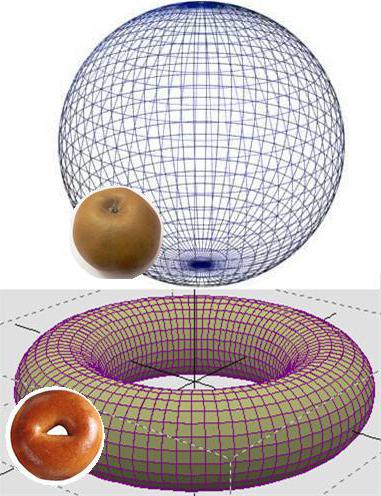
Co udowodnił Grzegorz Перельман
W 1900 roku znany naukowiec-filozof Henri Poincare zasugerował, że każda односвязное kompaktowe 3-wymiarowa rozmaitość bez krawędzi гомеоморфно 3-wymiarowej sferze. Jej dowód w ogólnym przypadku nie znajdowało się w ciągu wieku. Tylko w latach 2002-2003 petersburski matematyk R. Перельман opublikował szereg artykułów z rozwiązaniem problemu Poincare. Produkowali bomba. W 2010 roku hipoteza Poincare została wykluczona z listy «Nierozwiązane zadania» instytut Клэйя, a samemu Перельману zaproponowano uzyskać przysługujące mu znaczną wynagrodzenie, od którego ostatni odmówił, nie podając przyczyn swojej decyzji.
Najbardziej intuicyjne wyjaśnienie tego, co udało się udowodnić rosyjskiego matematyki, można dać, przedstawiając, że na obwarzanek (thor), naciągnęli gumowy twardy, a następnie próbują ściągnąć na krawędzi jego okręgu w jeden punkt. Oczywiście, że to niemożliwe. Inna sprawa, jeśli przeprowadzić ten eksperyment z piłką. W takim przypadku wydaje się być trójwymiarowa kula, wykonane z twardego, okrąg, którego ściągnęli do punktu hipotetycznym sznurkiem, będzie trójwymiarowej w rozumieniu zwykłego człowieka, ale dwuwymiarowej z punktu widzenia matematyki.
Poincare zasugerował, że trójwymiarowa kula jest jedynym trójwymiarowym «przedmiotem», powierzchnia, którą można ściągnąć w jeden punkt, a Перельману udało się to udowodnić. W ten sposób lista «Zawiłe zadania» dziś składa się z 6 problemów.

Teoria Younga-Millsa
Ta matematyczna problem zaproponowano jej autorami w 1954 roku. Naukowa sformułowanie teorii ma następującą postać: dla dowolnej prostej zwartej kalibracyjnej grupy kwantowej przestrzenna teoria, stworzona Young i Милльсом, istnieje, a przy tym ma zero defekt masy.
Jeśli mówić w języku zrozumiałym dla zwykłego człowieka, interakcji między naturalnych obiektów (cząstek, ciał, fale itp.) dzielą się na 4 rodzaje: elektromagnetyczne, grawitacyjne, słabe i silne. Już wiele lat fizycy próbują stworzyć ogólną teorię pola. Powinna ona stać się narzędziem do wyjaśnienia wszystkich tych interakcji. Teoria Younga-Mills ó to matematyczny język, za pomocą którego możliwe jest opisać 3 z 4 głównych sił natury. Ona nie dotyczy grawitacji. Dlatego nie można uznać, że Young i Millsa udało się stworzyć teorię pola.
Ponadto, nieliniowość zaproponowanych równań sprawia, że są one bardzo trudne do rozwiązania. Przy małych константах związku ich można w przybliżeniu rozwiązania w postaci szeregu teorii perturbacji. Jednak na razie nie jest jasne, jak można rozwiązać te równania w silnym związku.

Równania Naviera-Stokesa
Za pomocą tych wyrażeń opisuje procesy takie jak przepływ powietrza, przepływ płynów i turbulencje. Dla niektórych indywidualnych przypadkówanalityczne rozwiązania równania Naviera-Stokesa zostały już znalezione, jednak, aby to zrobić dla wspólnego razie nikomu się nie udało. W tym samym czasie, symulacje numeryczne dla konkretnych wartości prędkości, gęstości, ciśnienia, czasu, i tak dalej pozwala na osiągnięcie doskonałych wyników. Pozostaje mieć nadzieję, że ktoś będzie zastosować równania Naviera-Stokesa w odwrotnym kierunku, tzn. obliczyć z ich pomocą ustawienia, albo udowodnić, że metody rozwiązania nie ma.
Zadanie Берча ó Свиннертон-Farbiarski
Do kategorii «Nierozwiązane zadania» odnosi się hipoteza, zaproponowana przez angielskich naukowców z uniwersytetu w Cambridge. Jeszcze 2300 lat temu grecki uczony Эвклид dał pełny opis rozwiązań równania x2 + y2 = z2.
Jeśli dla każdej z liczb pierwszych policzyć ilość punktów na krzywej w jego modułu, będzie nieskończony zbiór liczb całkowitych. Jeśli konkretnym sposób «skleić» w 1 funkcję kompleksowego zmiennej, wtedy będzie zeta-funkcja Hassa-Weyla dla krzywej trzeciego rzędu, oznaczana literą L. zawiera Ona informacje na temat zachowania modulo wszystkich liczb pierwszych od razu.
Brian Birch i Peter Свиннертон-Dyer hipotezę odnośnie krzywych eliptycznych. Według niej, struktura i ilość wielu racjonalnych decyzji związane z zachowaniem L-funkcji w jednostce. Недоказанная w tej chwili hipoteza Берча ó Свиннертон-Farbiarski zależy od opisu równań stopnia 3 i jest jedynym stosunkowo proste wspólnym sposób obliczania stopnia krzywych eliptycznych.
Aby zrozumieć praktyczne znaczenie tego zadania, wystarczy powiedzieć, że we współczesnej kryptografii na krzywych eliptycznych opiera się cała klasa asymetrycznych systemów, a w ich stosowaniu są oparte krajowe standardy podpisu cyfrowego.

Równość klasy p i np
Jeśli reszta «Zadania tysiąclecia» odnoszą się do czysto matematycznym, to ta ma stosunek do aktualnej teorii algorytmów. Problem dotyczący równości klasy p i np, znany również, jako problem Cooka-Levina, zrozumiałym językiem może być sformułowana w następujący sposób. Załóżmy, że pozytywna odpowiedź na pewne pytanie można sprawdzić na tyle szybko, tj. za полиномиальное czas (PV). To prawda, czy twierdzenie, że odpowiedź na to można dość szybko znaleźć? Jeszcze łatwiejsze zadanie brzmi tak: czy rozwiązanie problemu sprawdzić nie trudniej, niż go znaleźć? Jeśli równość klasy p i np będzie kiedykolwiek udowodnione, to wszystkie problemy doboru będzie można brać się za NAWIEWU. W tej chwili wielu ekspertów wątpi w prawdziwość tego twierdzenia, chociaż nie można udowodnić w inny sposób.

Hipoteza Riemanna
Aż do 1859 roku nie stwierdzono żadnych prawidłowości, która opisuje, w jaki sposób przydzielane są liczby pierwsze wśród naturalnych. Być może było to związane z tym, że nauka zajmowała się innymi sprawami. Jednak w połowie 19 wieku sytuacja się zmieniła, i stały się one jednymi z najbardziej aktualnych, którymi zaczęłam się uczyć matematyki.
Hipoteza Riemanna, która pojawiła się w tym okresie ó to założenie o tym, że w rozkładzie liczb pierwszych istnieje pewna prawidłowość.
Dziś współcześni naukowcy uważają, że jeśli zostanie udowodnione, to będę musiał zmienić fundamentalne zasady współczesnej kryptografii, stanowiące podstawę znacznej części mechanizmów e-commerce.
Zgodnie z hipotezą Riemanna, charakter rozkładu liczb pierwszych, być może, znacznie różni się od planowanego w tej chwili. Rzecz w tym, że do tej na razie nie stwierdzono jakiegokolwiek systemu dystrybucji liczb pierwszych. Na przykład, istnieje problem óbliźniaków», różnica między nimi jest równa 2. Tymi liczbami są 11 i 13, 29. Inne proste liczby tworzą skupiska. To 101, 103, 107, itp. Naukowcy od dawna podejrzewali, że podobne skupiska istnieją i wśród bardzo dużych liczb pierwszych. Jeśli je znajdą, to trwałość nowoczesnych kluczy kryptograficznych będzie pod znakiem zapytania.

Hipoteza o cyklach Hodge ' a
Ten nierozwiązany do tej pory zadanie sformułowane w 1941 roku. Hipoteza Hodge ' a zakłada możliwość dopasowania kształtu dowolnego obiektu poprzez «klejenia» wraz prostych tel większym wymiarze. Ten sposób był znany i z powodzeniem stosowany jest od dawna. Nie wiadomo jednak, do jakiego stopnia można produkować uproszczenie.
Teraz już wiesz, jakie są zadania zawiłe istnieją w tej chwili. Są one przedmiotem badań tysięcy naukowców na całym świecie. Pozostaje mieć nadzieję, że w najbliższym czasie zostaną one rozwiązane, a ich praktyczne zastosowanie pomaga ludziom wyjść na nowy etap rozwoju technologicznego.
Article in other languages:
AR: https://tostpost.com/ar/education/1204-navier.html
HI: https://tostpost.com/hi/education/1204-navier--riemann.html
JA: https://tostpost.com/ja/education/1203-navier-stokes-hodge.html

Alin Trodden - autor artykułu, redaktor
"Cześć, jestem Alin Trodden. Piszę teksty, czytam książki, Szukam wrażeń. I nie jestem zły w opowiadaniu ci o tym. Zawsze chętnie biorę udział w ciekawych projektach."
Nowości
Uczelnie Rosji architektoniczne: ocena, opis, funkcje i opinie
Opracowanie planów i rysunków technicznych, wcielenie w życie wielkich projektów budowlanych, obróbka utworzonego obiektu i oddanie go do klienta – wszystko to obszar działalności zawodowej architektów. W tym artykule podaje...
Budowa komórki jajowej: ogólne informacje
komórka Jajowa ó to komórka płciowa samicy, która zawiera w sobie haploidalna zestaw chromosomów. Jej podstawowy cel ó przekazywanie informacji genetycznej w czasie zapłodnienia. Budowa komórki jajowej w naturze mogą...
Сословно-reprezentacyjna monarchia jako forma administracji publicznej
Monarchia odnosi się do liczby dawnych form panowania. Jej osobliwość polega na tym, że władzę nad wszystkimi sferami państwa należy do jednej osoby na prawo престолонаследования. W dawnych czasach wierzono, że monarcha ó p...
Analiza działalności gospodarczej – jest to system technik, opracowany przez naukową metodą, dzięki której staje się możliwe nauka ekonomii przedsiębiorstwa. Z jego użyciem są rezerwy produkcyjne zgodnie z отчетными i kont i...
Moment bezwładności. Niektóre szczegóły mechaniki ciała stałego
Jednym z podstawowych właściwości fizycznych zasad współdziałania ciał stałych jest prawo bezwładności, sformułowaną jeszcze wielkim Izaakiem Newtonem. Z tym pojęciem mamy do czynienia praktycznie stale, tak jak to ma bardzo duży ...
1147 rok - jaki to wiek dla kształtowania Moskwy?
W «Panteonie Rosyjskich władców» zawiera informacje o tym, że pierwsze plemiona na terenie współczesnej Moskwy opanowali te ziemie jeszcze w 880 roku. Wielu naukowców zadaje sobie pytanie: 1147 rok - jaki to wiek dla k...




















Uwaga (0)
Ten artykuł nie ma komentarzy, bądź pierwszy!