Now - 17:29:38
Unsolvable problems: the Navier-Stokes equations, the Hodge conjecture, the Riemann hypothesis. The Millennium goals
Impossible task — the 7 most interesting mathematical problems. Each of them was proposed by famous scientists, as a rule, in the form of hypotheses. For many decades, over their decision to break the head of mathematics in the world. Those who succeed, are rewarded with a million dollars offered by the Institute Claa.
Prehistory
In 1900 the great German mathematician-universal David Hilbert presented a list of 23 problems.
Studies carried out with the aim of solving them, has had an enormous influence on 20th century science. At the moment most of them have ceased to be riddles. Among the unresolved or partially resolved is left:
- The problem of consistency of the arithmetical axioms;
- A General law of reciprocity in the space of any numerical field;
- A mathematical study of the physical axioms;
- The study of quadratic forms with arbitrary algebraic number coefficients;
- The problem rigorously escalerillas geometry Fedor Schubert;
- Etc.
Unexplored are: the problem of distribution in any algebraic field of rationality-known theorem of Kronecker and Riemann hypothesis.
Institute Kleya
Under the title of a famous private non-profit organization, which headquarters is located in Cambridge, Massachusetts. It was founded in 1998 by a Harvard mathematician A. Jaffe and businessman L. Claim. The aim of the Institute is the promotion and development of mathematical knowledge. To achieve this, the organization gives awards to scientists and sponsors promising research.
Recommended
"Knowledge is light and ignorance is darkness": the value, meaning and alternatives
There are some sayings that would seem to need no explanation, such as “teaching & ndash; light and ignorance – darkness”. But some still do not understand their meaning. But not only for such people is written by our article. I...
What was invented by Mendeleev for the army. The history and fate of the invention
D. I. Mendeleev was a brilliant Russian scientist-polymath, who made many important discoveries in various fields of science and technology. Many people know that he is the author of “Fundamentals of chemistry" and the periodic law of chem...
The origin of the Slavs. The influence of different cultures
Slavs (under this name), according to some researchers, appeared in the story only in 6 century ad. However, the language of nationality bears the archaic features of the Indo-European community. This, in turn, suggests that the origin of the Slavs h...
In the early 21st century Cleia Mathematical Institute offered a prize to those who solve the problem, which is known as the most complex unsolvable problems, calling its list of Millennium Prize Problems. From “List of Gilbert” it includes only the Riemann hypothesis.
The Millennium goals
In the list of the Institute Klaa initially included:
- The hypothesis on the Hodge cycles;
- The equations of quantum theory Yang-mills;
- The poincaré conjecture;
- The problem of equality of classes P and NP;
- The Riemann hypothesis;
- Navier-Stokes equations, the existence and smoothness of its decisions;
- Problem birch — Swinnerton-Dyer.
These open mathematical problems are of great interest, since they can have numerous practical implementations.
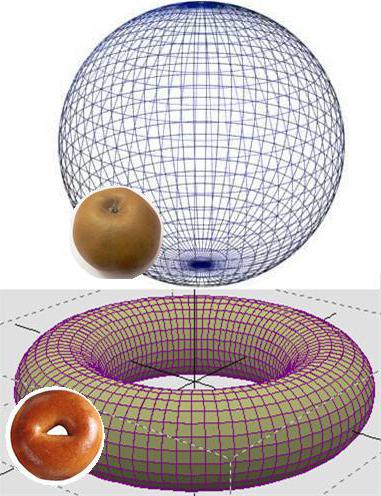
Proved by Grigory Perelman
In 1900, the famous scientist and philosopher, Henri poincaré suggested that every simply connected compact 3-dimensional manifold without edge is homeomorphic to the 3-dimensional sphere. Its proof in the General case was not for a century. Only in 2002-2003, the St. Petersburg mathematician G. Perelman published a series of articles with the solution of the Poincare problem. They produced a bombshell. In 2010, the poincaré conjecture was excluded from the list of “challenges” of the Institute Kleya, and most Perelman was invited to due to him a considerable reward, which the latter refused, without explaining the reasons for its decision.
The Most clear explanation of what failed to prove Russian math, you can give, imagine what a bagel (torus), pull the rubber disk, and then try to pull the edge of its circumference at one point. Obviously, that's impossible. Another thing, if you make this experiment with the globe. In this case, it seems to be a three-dimensional sphere obtained from a disk, the circumference of which is pulled to the point of a hypothetical cord is three-dimensional in the understanding of an ordinary person, but two-dimensional from the point of view of mathematics.
Poincare suggested that the three-dimensional sphere is the only three-dimensional “subject”, the surface of which can be contracted to one point, and Perelman was able to prove it. Thus, a list of “Unsolvable” today, consists of 6 problems.

Yang-mills
This math problem was proposed by its authors in 1954-m to year. The scientific formulation of the theory has the following form: for any simple compact gauge group of quantum spatial theory created by Yang and Millsom exists and has a zero mass defect.
If you speak the language that is understandable to the average person, the interaction between the natural objects (particles, bodies, waves, etc.) are divided into 4 types: electromagnetic, gravitational, weak and strong. For many years physicists have been trying to create a General field theory. It should be a tool to account for all these interactions. The theory of Yang-mills — is a mathematical language with which to describe 3 of the 4 fundamental forces of nature. It is not applicable to gravity. Therefore, it cannot be assumed that Yang and Mills were able to create field theory.
In addition, the proposed nonlinearity of the equations makes them extremely difficult to solve. For small constants when they can approximately be solved in the form of a perturbation series. However, it is unclear how it is possible to solve these equations at strong communication.

The Navier-Stokes Equations
Using these expressions describe processes such as air flow, for liquids and turbulence. For some particular cases analytical solutions of the Navier-Stokes equations have already been found, but to do it for the common yet no one has. At the same time, numerical simulation for specific values of velocity, density, pressure, time and so on allows us to achieve excellent results. It is hoped that someone will be able to apply the Navier-Stokes equations in the opposite direction, i.e. to calculate the parameters, or to prove that the method is no solution.
The Task of birch — Swinnerton-Dyer
The category of “challenges” refers to the hypothesis proposed by English scientists from the University of Cambridge. 2300 years ago the ancient Greek scholar Euclid gave a complete description of the solutions of the equation x2 + y2 = z2.
If for each of the primes is to count the number of points on a curve in his module, you get an infinite set of integers. If a particular way “glue” it into 1 function of a complex variable, then get the Zeta function and Hasse-Weil for cubic curve, denoted by the letter L. It contains information about the behavior modulo all primes at once.
Brian birch and Peter Swinnerton-Dyer has put forward a hypothesis regarding elliptic curves. According to her, the structure and number of many rational solutions associated with the behavior of L-functions in the unit. Unproven at the moment, the hypothesis of birch — Swinnerton-Dyer depends on the description of algebraic equations degree 3 and is the only comparatively simple General method for computing the rank of elliptic curves.
To understand the practical importance of this task, suffice it to say that in modern cryptography based on elliptic curves an entire class of asymmetric systems, and the use of domestic standards-based digital signatures.

The p versus np
If the rest of the "Millennium goals" belong to the purely mathematical, then this is relevant to the theory of algorithms. The issue of equality of classes p and np, also known as the problem of cook-Levin and simple language can be formulated as follows. Suppose that a positive answer to a question can be checked quite quickly, i.e. in polynomial time (PV). Then it correct to assert that the answer can be quite fast to find? Even easier, this task sounds so: whether really the solution of the problem test is not more difficult than to find it? If the equality of the classes p and np will ever be proven, then all the problems of selection can be solved for PV. At the moment, many specialists doubt the truth of this statement, though I can't prove otherwise.

Riemann Hypothesis
Until 1859 there was not detected any regularities which would describe how Prime numbers are distributed among natural. Perhaps it was due to the fact that science was engaged in other matters. However, by the mid-19th century the situation changed, and they became one of the most relevant, which began to engage in mathematics.
The Riemann Hypothesis emerged in this period — is the assumption that the distribution of Prime numbers there is a definite pattern.
Today, many modern scholars believe that if it is proved, we will have to reconsider many fundamental principles of modern cryptography, the backbone of a significant part of e-Commerce.
According to the Riemann hypothesis, the nature of distribution of Prime numbers, perhaps significantly differs from the intended at the moment. The fact is that up to now have not yet been discovered any system in the distribution of Prime numbers. For example, there is the problem of ‘the twins”, the difference between which is equal to 2. These numbers are 11 and 13, 29. Other Prime numbers form clusters. This ...
Article in other languages:
AR: https://tostpost.com/ar/education/1204-navier.html
HI: https://tostpost.com/hi/education/1204-navier--riemann.html
JA: https://tostpost.com/ja/education/1203-navier-stokes-hodge.html

Alin Trodden - author of the article, editor
"Hi, I'm Alin Trodden. I write texts, read books, and look for impressions. And I'm not bad at telling you about it. I am always happy to participate in interesting projects."
Related News
Who discovered the phenomenon of radioactivity and how it happened?
the article tells about who discovered the phenomenon of radioactivity, when it happened and under what circumstances.Radioactivitythe Modern world and the industry is unlikely to be able to do without nuclear energy. Nuclear reac...
Doctor of philosophy Yuri Levada: the biography, scientific activity
Professor Levada, Yuri Alexandrovich-an outstanding Soviet, Russian and Ukrainian sociologist. Thanks to his efforts, the sociology of dogmatic, ideological and theoretical transformed into a modern practical science that allows d...
What is the relationship between beauty and use in life
Happy heart, soul and eyesLife, beauty and coolness.God created this world for us.What else do we need to be happy!Everything in nature wisely invented. This took care of the Creator. We can not only observe a correlation between ...
The meaning of the word "fool": the ancient and modern meaning of the noun
Probably every person in your address ever heard that word. It is remarkable in all respects: firstly, it is structurally unstable expletive (although how you look), and secondly, he has a second sense, and in the third, sometimes...
How to recognize the symptoms of hyperactive child
recently we often hear the phrase " My kid is so hyperactive!" from moms to the restless child. But few of them thought that ADHD (attention deficit and hyperactivity disorder) is a diagnosis, not empty words. So, if you're concer...
All about mutations. Evolutionary role
Mutation is called persistent changes in the genotype that occur due to the influence of external and internal factors. The ancestor of the term is Hugo de Vries-Dutch botanist and geneticist. The process, when the mutation is cal...






















Comments (0)
This article has no comment, be the first!