Now - 16:10:32
Вирішуються завдання: рівняння Нав'є-Стокса, гіпотеза Ходжа, гіпотеза Рімана. Завдання тисячоліття
Вирішуються завдання — це 7 цікавих математичних проблем. Кожна з них була запропонована свого часу відомими вченими, як правило, у вигляді гіпотез. Ось вже багато десятиліть над їх вирішенням ламають голови математики у всьому світі. Тих, хто доб'ється успіху, чекає винагорода в один мільйон американських доларів, запропоноване інститутом Клэйя.
Передісторія
В 1900 році великий німецький математик-універсал давида Гільберта, представив список з 23-х проблем.
Дослідження, здійснені з метою їх вирішення, справили величезний вплив на науку 20 століття. На даний момент більшість з них вже перестали бути загадками. Серед невирішених або частково вирішених залишилися:
- проблема несуперечності арифметичних аксіом;
- загальний закон взаємності на просторі будь-якого числового поля;
- математичне дослідження фізичних аксіом;
- дослідження квадратичних форм при довільних алгебраїчних числових коефіцієнтів;
- проблема суворого обґрунтування исчислительной геометрії Федора Шуберта;
- та ін
Недослідженими є: проблема розповсюдження на будь-яку алгебраїчну область раціональності відомої теореми Кронекера і гіпотеза Рімана.
Інститут Клэйя
Під такою назвою відома приватна некомерційна організація, штаб-квартира якої знаходиться в Кембриджі, штат Массачусетс. Вона була заснована в 1998 році гарвардським математиком А. Джеффі і бізнесменом Л. Клэйем. Метою діяльності інституту є популяризація та розвиток математичних знань. Для її досягнення організація видає премії вченим і спонсорує багатообіцяючі дослідження.
Більше:
Перший штучний супутник Землі є одним з найбільших досягнень науки ХХ століття. Тим не менш, як це ні парадоксально, цьому великому науковому і технічному досягненню значною мірою сприяла холодна війна між двома наддержавами: США і Радянським Союзом....
Що таке соціалізація, і як вона змінює людину
Спробуємо розібратися, що таке соціалізація, в чому її сутність і особливість. Адже для кожної особистості входження у суспільство і засвоєння його основних норм є фундаментом до подальшої безпроблемною і успішного життя і діяльності. Отже, що таке с...
Принц Чарльз – головний спадкоємець британського престолу
Згідно із законом королівства Великобританія, спадкоємець британського престолу - це старший закононароджена син чинного монарха або ж попереднього претендента на престол. Однак якщо у царюючого особи немає дитини чоловічої статі, то право спадкуванн...
На початку 21 століття Математичний інститут Клэйя запропонував премію тим, хто вирішить проблеми, які відомі, як вирішуються найскладніші завдання, назвавши свій список Millennium Prize Problems. З «Списку Гільберта» в нього увійшла тільки гіпотеза Рімана.
Завдання тисячоліття
список інституту Клэйя спочатку входили:
- гіпотеза про циклах Ходжа;
- рівняння квантової теорії Янга — Міллса;
- гіпотеза Пуанкаре;
- проблема рівності класів Р і NP;
- гіпотеза Рімана;
- рівняння Нав'є Стокса, про існування і гладкості його рішень;
- проблема Берча — Свиннертон-Дайєра.
Ці відкриті математичні проблеми представляють величезний інтерес, оскільки можуть мати безліч практичних реалізацій.
довів Григорій Перельман
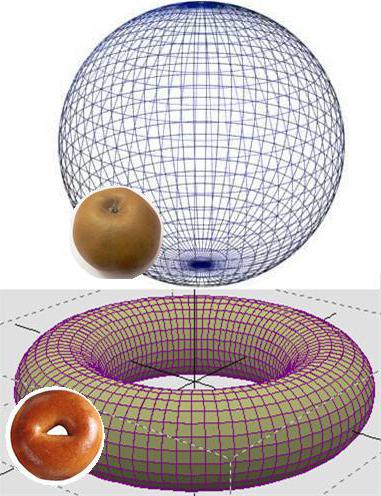
В 1900 році відомий вчений-філософ Анрі Пуанкаре припустив, що всяке односвязное компактна 3-мірне різноманіття без краю гомеоморфно 3-мірної сфері. Її доказ в загальному випадку не знаходилося протягом століття. Лише в 2002-2003 роках петербурзький математик Р. Перельман опублікував ряд статей з вирішенням проблеми Пуанкаре. Вони справили ефект бомби, що розірвалася. У 2010 році гіпотеза Пуанкаре була виключена зі списку «Невирішені завдання» інституту Клэйя, а самому Перельману було запропоновано отримати належне йому чималу винагороду, від якого останній відмовився, не пояснивши причин свого рішення.
Саме зрозуміле пояснення того, що вдалося довести російському математику, можна дати, уявивши, що на бублик (тор), натягують гумовий диск, а потім намагаються стягнути краї його окружності в одну точку. Очевидно, що це неможливо. Інша справа, якщо провести цей експеримент з кулею. В такому випадку начебто тривимірна сфера, вийшла з диска, окружність якого стягнули в точку гіпотетичним шнуром, буде тривимірної у розумінні пересічної людини, але двовимірної з точки зору математики.
Пуанкаре припустив, що тривимірна сфера є єдиним тривимірним «предметом», поверхня якої можна стягнути в одну точку, а Перельману вдалося це довести. Таким чином, список «Вирішуються задачі» сьогодні складається з 6 проблем.

Теорії Янга-Міллса
Ця математична проблема була запропонована її авторами в 1954-му році. Наукова формулювання теорії має наступний вигляд: для будь-простий компактної калібрувальної групи квантова просторова теорія, створена Янгом і Милльсом, існує, і при цьому має нульовий дефект маси.
Якщо говорити мовою, зрозумілою для звичайної людини, взаємодії між природними об'єктами (частками, тілами, хвилями тощо) діляться на 4 типи: електромагнітна, гравітаційна, слабка і сильна. Вже багато років фізики намагаються створити загальну теорію поля. Вона повинна стати інструментом для пояснення всіх цих взаємодій. Теорія Янга-Міллса — це математичний мову, з допомогою якого стало можливо описати 3 з 4-х основних сил природи. Вона не застосовується до гравітації. Тому не можна вважати, що Янга та Міллсу вдалося створити теорію поля.
Крім того, нелінійність запропонованих рівнянь робить їх вкрай складними для вирішення. При малих константи зв'язку їх вдається наближено вирішити у вигляді ряду теорії збурень. Проте поки незрозуміло, як можна вирішити ці рівняння при сильного зв'язку.

Рівняння Нав'є-Стокса
З допомогою цих виразів описуються такі процеси, як повітряні потоки, протягом рідин і турбулентність. Для деяких окремих випадківаналітичні розв'язки рівняння Нав'є-Стокса вже були знайдені, однак зробити це для загального поки нікому не вдалося. У той же час, чисельне моделювання для конкретних значень швидкості, щільності, тиску, часу і так далі дозволяє домогтися прекрасних результатів. Залишається сподіватися, що у кого-небудь вийде застосувати рівняння Нав'є-Стокса в зворотному напрямку, тобто обчислити з їх допомогою настройки, або довести, що методу рішення немає.
Завдання Берча — Свиннертон-Дайєра
До категорії «Невирішені завдання» відноситься і гіпотеза, запропонована англійськими науковцями з Кембриджського університету. Ще 2300 років тому давньогрецький учений Евклід дав повний опис розв'язків рівняння x2 + y2 = z2.
Якщо для кожного з простих чисел порахувати кількість точок на кривій за його модулю, вийде нескінченний набір цілих чисел. Якщо конкретним чином «склеїти» 1 функцію комплексної змінної, тоді вийде дзета-функція Хассе-Вейля для кривої третього порядку, що позначається буквою L. Вона містить інформацію про поведінку по модулю всіх простих чисел відразу.
Брайан Берч і Пітер Свиннертон-Дайер висунули гіпотезу щодо еліптичних кривих. Згідно їй, структура і кількість безлічі її раціональних рішень пов'язані з поведінкою L-функції в одиниці. Недоведена на даний момент гіпотеза Берча — Свиннертон-Дайєра залежить від опису алгебраїчних рівнянь 3 ступеня і є єдиним порівняно простим загальним способом розрахунку рангу еліптичних кривих.
Щоб зрозуміти практичну важливість цього завдання, досить сказати, що в сучасній криптографії на еліптичних кривих заснований цілий клас асиметричних систем, і їх застосування засновані вітчизняні стандарти цифрового підпису.

Рівність класів p і np
Якщо решта «Завдання тисячоліття» відносяться до чисто математичним, то ця має відношення до актуальної теорії алгоритмів. Проблема, що стосується рівності класів р і np, відома також, як проблема Кука-Левіна, зрозумілою мовою може бути сформульована наступним чином. Припустимо, що позитивну відповідь на якесь питання можна перевірити досить швидко, тобто за полиномиальное час (ПВ). Тоді правильно твердження, що відповідь на нього можна досить швидко відшукати? Ще простіше це завдання звучить так: чи дійсно рішення завдання перевірити не важче, ніж його знайти? Якщо рівність класів р і np буде коли-небудь доведено, то всі проблеми підбору можна буде вирішувати за ПВ. На даний момент багато фахівців сумніваються в істинності цього твердження, хоча не можуть довести зворотне.

Гіпотеза Рімана
Аж до 1859 року не було виявлено будь-якої закономірності, яка описувала б, як прості числа розподіляються серед натуральних. Можливо, це було пов'язано з тим, що наука займалася іншими питаннями. Однак до середини 19 століття ситуація змінилася, і вони стали одними з найбільш актуальних, якими почала займатися математика.
Гіпотеза Рімана, що з'явилася в цей період — це припущення про те, що розподіл простих чисел існує певна закономірність.
Сьогодні багато сучасні вчені вважають, що якщо вона буде доведена, то доведеться переглянути багато фундаментальні принципи сучасної криптографії, що становлять основу значної частини механізмів електронної комерції.
Відповідно до гіпотези Рімана, характер розподілу простих чисел, можливо, суттєво відрізняється від передбачуваного на даний момент. Справа в тому, що до цього поки не було виявлено будь-якої системи розподілу простих чисел. Наприклад, існує проблема «близнюків», різниця між якими дорівнює 2. Цими числами є 11 і 13, 29. Інші прості числа утворюють скупчення. Це 101, 103, 107 та ін. Вчені давно підозрювали, що подібні скупчення існують і серед дуже великих простих чисел. Якщо їх знайдуть, то стійкість сучасних криптоключів опиниться під питанням.

Гіпотеза про циклах Ходжа
Ця невирішена досі задача сформульована в 1941 році. Гіпотеза Ходжа передбачає можливість апроксимації форми будь-якого об'єкта шляхом «склеювання» разом простих тіл більшої розмірності. Цей спосіб був відомий і успішно застосовується досить давно. Однак не відомо, до якої міри можна виробляти спрощення.
Тепер ви знаєте, які вирішуються задачі існують на даний момент. Вони є предметом дослідження тисяч вчених у всьому світі. Залишається сподіватися, що найближчим часом вони будуть вирішені, а їх практичне застосування допоможе людству вийти на новий виток технологічного розвитку.
Article in other languages:
AR: https://tostpost.com/ar/education/1204-navier.html
HI: https://tostpost.com/hi/education/1204-navier--riemann.html
JA: https://tostpost.com/ja/education/1203-navier-stokes-hodge.html

Alin Trodden - автор статті, редактор
"Привіт, Я Алін Тродден. Я пишу тексти, читаю книги і шукаю враження. І я непогано вмію розповідати вам про це. Я завжди радий брати участь у цікавих проектах."
Новини
Вузи Росії архітектурні: рейтинг, опис, особливості та відгуки
Розробка інженерних планів і креслень, втілення в життя грандіозних будівельних проектів, доробка створеного об'єкта та здача його замовникові – все це галузь професійної діяльності архітекторів. У цій статті ми перерахуємо ...
Будова яйцеклітини: загальна інформація
Яйцеклітина — це статева клітина самки, яка містить в собі гаплоїдний набір хромосом. Її основне призначення — передача генетичної інформації під час запліднення. Будова яйцеклітини в природі може бути найрізноманітніш...
Станово-представницька монархія як форма державного управління
Монархія належить до числа древніх форм правління. Її особливість полягає в тому, що влада над усіма сферами держави належить одній особі на праві успадкування престолу. У давні часи вважалося, що монарх – помазаник Божий. О...
Аналіз господарської діяльності – це система прийомів, розроблена науковим методом, завдяки якій стає можливим вивчення економіки підприємства. З його допомогою виявляються виробничі резерви згідно із звітними і обліковими д...
Момент інерції. Деякі подробиці механіки твердого тіла
Одним з основних фізичних принципів взаємодії твердих тіл є закон інерції, сформульований ще великим Ісааком Ньютоном. З цим поняттям ми стикаємося практично постійно, так як воно має надзвичайно великий вплив на всі матеріальні п...
1147 рік - це вік для становлення Москви?
«Пантеоні Російських государів» міститься інформація про те, що перші племена на території сучасної Москви освоювали ці землі ще в 880-му році. Багато вчених задаються питанням: 1147 рік - це вік для становлення Російс...






















Примітка (0)
Ця стаття не має коментарів, будьте першим!