न सुलझा हुआ समस्याओं: Navier-स्टोक्स समीकरण, हॉज अनुमान है, Riemann परिकल्पना है. सहस्राब्दी लक्ष्यों

असंभव कार्य — 7 सबसे दिलचस्प गणितीय समस्याओं. उनमें से प्रत्येक के द्वारा प्रस्तावित किया गया था प्रसिद्ध वैज्ञानिकों, एक नियम के रूप में, के रूप में hypotheses. कई दशकों के लिए, पर अपने निर्णय को तोड़ने के लिए सिर में गणित की दुनिया है. जो उन लोगों, सफल होने के लिए पुरस्कृत कर रहे हैं के साथ एक मिलियन डॉलर की पेशकश की संस्थान द्वारा Claa.

प्रागितिहास

1900 में महान जर्मन गणितज्ञ-यूनिवर्सल डेविड हिल्बर्ट की एक सूची प्रस्तुत 23 समस्याओं.

किए गए अध्ययन के उद्देश्य के साथ उन्हें हल है, पर एक भारी प्रभाव पड़ा 20 वीं सदी के विज्ञान है. फिलहाल उनमें से ज्यादातर समाप्त किया जा करने के लिए पहेलियों । के बीच अनसुलझे या आंशिक रूप से हल हो गई है छोड़ दिया है:

• समस्या की स्थिरता के अंकगणितीय axioms;
• एक सामान्य कानून के आदान-प्रदान की अंतरिक्ष में किसी भी संख्यात्मक फ़ील्ड के लिए;
• एक गणितीय अध्ययन के भौतिक axioms;
• के के अध्ययन के द्विघात रूपों के साथ मनमाना संख्या बीजीय coefficients;
• समस्या का कड़ाई से ग्वाडेलूप विक्टोरीया ज्यामिति Fedor Schubert;
• आदि

बेरोज़गार हैं: समस्या के वितरण में किसी भी बीजीय क्षेत्र की समझदारी प्रसिद्ध प्रमेय के Kronecker और Riemann परिकल्पना है.

संस्थान Kleya

के शीर्षक के अंतर्गत एक प्रसिद्ध निजी गैर-लाभकारी संगठन है, जिसका मुख्यालय स्थित है में कैम्ब्रिज, मैसाचुसेट्स. यह स्थापित किया गया था 1998 में एक हार्वर्ड गणितज्ञ ए Jaffe और व्यापारी एल का दावा है. उद्देश्य संस्थान के संवर्धन और विकास के गणितीय ज्ञान है. इस प्राप्त करने के लिए, संगठन देता है पुरस्कार के लिए वैज्ञानिकों और प्रायोजकों होनहार शोध है.

अधिक:

प्राकृतिक आदमी की जरूरतों: प्रकार के और तरीके को पूरा करने के लिए

प्राकृतिक आदमी की जरूरतों कई हैं । के रूप में और सामाजिक. यह मानव स्वभाव है करने के लिए कभी भी जरूरत है. और जब वह लगता है के लिए एक तीव्र आवश्यकता में कुछ भी है, वह कोशिश करता है को संतुष्ट करने के लिए. हालांकि, क्रम में सब कुछ.अवधारणाइससे पहले कि मै...

नाम के महीने में यूक्रेनी भाषा

नाम के महीने में यूक्रेनी और अलग अलग भाषाओं में स्पष्ट है अलग ढंग से. कई स्लाव भाषाओं में, वे समान हैं । चलो देखते हैं कि कैसे अलग-अलग नाम हैं, मौसम के अलग अलग देशों में.का नाम महीने में यूक्रेनीमें यूक्रेनी भाषा के नाम पर वर्ष के प्रत्येक महीने के ल...

निबंध के लिए "बुद्धि से हाय": क्यों इस खेल के लिए प्रासंगिक आधुनिक समाज?

A. S. Griboyedov लिखा एक नाटक बन गया है, जो नींव के शास्त्रीय रूसी साहित्य । उस में, वह बहुत सही रूप में वर्णित सामाजिक बुराइयों निहित हैं कि आधुनिक समाज में. इसलिए, निबंध का उत्पाद है "बुद्धि से हाय" अनिवार्य है स्कूल के पाठ्यक्रम में.के बारे में सं...

जल्दी 21 वीं सदी में Cleia गणितीय संस्थान की पेशकश की एक पुरस्कार जो उन लोगों के लिए समस्या का समाधान है, जो जाना जाता है के रूप में सबसे जटिल से न सुलझा हुआ समस्याओं, फोन की अपनी सूची में मिलेनियम पुरस्कार समस्याओं. से “की सूची गिल्बर्ट” यह भी शामिल है केवल Riemann परिकल्पना है.

सहस्राब्दी लक्ष्यों

सूची में संस्थान के Klaa शुरू में शामिल हैं:

इन खुले गणितीय समस्याओं कर रहे हैं महान ब्याज की है, के बाद से वे कर सकते हैं कई व्यावहारिक implementations.

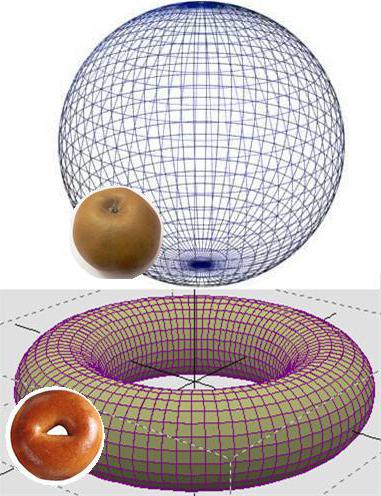
ने साबित कर दिया Grigory Perelman

1900 में, प्रसिद्ध वैज्ञानिक और दार्शनिक, हेनरी पोंकारे सुझाव दिया कि हर बस से जुड़े कॉम्पैक्ट 3-आयामी कई गुना के बिना बढ़त है homeomorphic के लिए 3 आयामी क्षेत्र है. इसके सबूत में सामान्य मामला नहीं था एक सदी के लिए. केवल 2002-2003 में, सेंट पीटर्सबर्ग गणितज्ञ जी Perelman प्रकाशित लेख की एक श्रृंखला के साथ समाधान के Poincare समस्या है । वे उत्पादित एक धमाके है. 2010 में, पोंकारे अनुमान था की सूची से बाहर रखा “चुनौतियों” संस्थान के Kleya, और सबसे Perelman आमंत्रित किया गया था करने के लिए कारण उसे करने के लिए एक काफी इनाम है, जो के उत्तरार्द्ध से इनकार कर दिया कारणों को स्पष्ट बिना, अपने निर्णय के लिए.

सबसे स्पष्ट विवरण के क्या साबित करने में विफल रूसी गणित, आप दे सकते हैं, कल्पना कीजिए कि एक bagel (टोरस), रबर खींच डिस्क, और उसके बाद की कोशिश करने के लिए पुल के किनारे इसकी परिधि पर एक बिंदु. जाहिर है, यह असंभव है. एक और बात, अगर आप इस के साथ प्रयोग । इस मामले में, यह करने के लिए लगता है एक तीन आयामी क्षेत्र से प्राप्त एक डिस्क, परिधि, जिनमें से खींच लिया है करने के लिए बिंदु के एक काल्पनिक रस्सी है, तीन आयामी की समझ में एक साधारण व्यक्ति है, लेकिन दो आयामी देखने के बिंदु से गणित के.

Poincare सुझाव दिया है कि तीन आयामी क्षेत्र है, केवल तीन आयामी “विषय”, सतह के लिए हो सकता है, जो अनुबंध करने के लिए एक बिंदु है, और Perelman में सक्षम था यह साबित करने के लिए है । इस प्रकार, की एक सूची “न सुलझा हुआ” आज, के होते हैं 6 समस्याओं.

यांग मिल्स

इस गणित समस्या द्वारा प्रस्तावित किया गया था इसके लेखक 1954 में-मीटर करने के लिए वर्ष. वैज्ञानिक निर्माण के सिद्धांत निम्नलिखित फार्म है: के लिए किसी भी साधारण कॉम्पैक्ट गेज के क्वांटम स्थानिक सिद्धांत के द्वारा बनाई गई यांग और Millsom मौजूद है और एक शून्य द्रव्यमान का दोष है.

यदि आप भाषा बोलते समझा जा सकता है कि औसत व्यक्ति के लिए, के बीच बातचीत को प्राकृतिक वस्तुओं (कणों, शरीर, लहरें, आदि.) 4 प्रकार में विभाजित हैं: विद्युत चुम्बकीय, गुरुत्वाकर्षण, कमजोर और मजबूत है । कई वर्षों के लिए भौतिकविदों की कोशिश कर रहा है बनाने के लिए एक सामान्य सिद्धांत के क्षेत्र में. यह होना चाहिए करने के लिए एक उपकरण के लिए खाते में इन सभी बातचीत की है । के सिद्धांत यांग मिल्स — एक गणितीय भाषा के साथ जो वर्णन करने के लिए 3 से 4 मौलिक प्रकृति के बलों. यह के लिए लागू नहीं है, गुरुत्वाकर्षण है । इसलिए, यह नहीं किया जा सकता है कि माना जाता यांग और मिलों में सक्षम थे बनाने के लिए क्षेत्र सिद्धांत है.

इसके अलावा, प्रस्तावित nonlinearity के समीकरण बनाता है उन्हें बहुत मुश्किल हल करने के लिए । छोटे के लिए स्थिरांक जब वे कर सकते हैं लगभग हल किया जा सकता है के रूप में एक गड़बड़ी श्रृंखला है । हालांकि, यह स्पष्ट नहीं है कि यह कैसे संभव है हल करने के लिए इन समीकरणों में मजबूत संचार.

Navier-स्टोक्स समीकरण

का उपयोग कर इन भाव प्रक्रियाओं का वर्णन इस तरह के रूप में हवा का प्रवाह, तरल पदार्थ के लिए और अशांति है । के लिए कुछ विशेष मामलों मेंविश्लेषणात्मक समाधान के Navier-स्टोक्स समीकरण है पहले से ही पाया गया है, लेकिन यह करने के लिए आम आदमी के लिए अभी तक कोई नहीं गया है. एक ही समय में, संख्यात्मक सिमुलेशन के लिए विशिष्ट मूल्यों के वेग, घनत्व, दबाव, समय और इतने पर करने के लिए हमें की अनुमति देता है उत्कृष्ट परिणाम प्राप्त. यह आशा व्यक्त की है कि किसी सक्षम हो जाएगा लागू करने के लिए Navier-स्टोक्स समीकरण के विपरीत दिशा में, यानी करने के लिए मापदंडों की गणना, या करने के लिए साबित होता है कि विधि का कोई समाधान नहीं है.

का कार्य सन्टी और mdash; Swinnerton-डायर

की श्रेणी “चुनौतियों” करने के लिए संदर्भित करता परिकल्पना द्वारा प्रस्तावित हिन्दी विश्वविद्यालय से वैज्ञानिकों के कैम्ब्रिज. 2300 साल पहले प्राचीन यूनानी विद्वान यूक्लिड ने एक पूर्ण विवरण के समाधान के समीकरण x2 + y2 = z2.

आप में से प्रत्येक के लिए primes के लिए है की संख्या गिनती बिंदुओं पर एक वक्र में अपने मॉड्यूल के साथ, आप एक अनंत सेट integers. अगर एक खास तरह “गोंद” इसे में 1 का कार्य एक जटिल चर, तो जीटा समारोह और Hasse-Weil के लिए घन वक्र, द्वारा चिह्नित पत्र एल के बारे में जानकारी है व्यवहार सापेक्ष सभी primes में एक बार.

ब्रायन सन्टी और पीटर Swinnerton-डायर को आगे रखा एक परिकल्पना के बारे में अण्डाकार curves. अनुसार उसे करने के लिए, संरचना और संख्या के कई तर्कसंगत समाधान के व्यवहार के साथ जुड़े L-कार्यों में इकाई है । अप्रमाणित फिलहाल, परिकल्पना के सन्टी और mdash; Swinnerton-डायर पर निर्भर करता है के विवरण के बीजीय समीकरणों की डिग्री 3 और केवल अपेक्षाकृत सरल सामान्य विधि के लिए कंप्यूटिंग के रैंक अण्डाकार curves.

समझने के लिए व्यावहारिक महत्व के इस कार्य के लिए, यह कहने के लिए पर्याप्त है कि में आधुनिक क्रिप्टोग्राफी पर आधारित अण्डाकार curves एक पूरे वर्ग के असममित सिस्टम, और घरेलू मानकों पर आधारित डिजिटल हस्ताक्षरों.

पी बनाम np

अगर बाकी की "सहस्राब्दी लक्ष्यों" करने के लिए संबंधित विशुद्ध रूप से गणितीय, तो इस के लिए प्रासंगिक है के सिद्धांत एल्गोरिदम. मुद्दे की समानता की कक्षाओं पी और एनपी भी जाना जाता है, समस्या के रूप में के लिए कुक-लेविन और सरल भाषा में तैयार किया जा सकता है के रूप में इस प्रकार है । मान लीजिए कि एक सकारात्मक एक सवाल के जवाब जाँच की जा सकती है काफी जल्दी है, यानी बहुपद समय में (पीवी). तो यह सही करने के लिए जोर है कि जवाब हो सकता है काफी तेजी से खोजने के लिए? यहां तक कि आसान है, इस कार्य लगता है तो: क्या वास्तव में समस्या के समाधान का परीक्षण नहीं है की तुलना में अधिक मुश्किल इसे खोजने के लिए? अगर समानता की कक्षाओं पी और एनपी कभी भी हो जाएगा सिद्ध है, तो सभी समस्याओं का चयन कर सकते हैं हल करने के लिए पी. वी. फिलहाल, कई विशेषज्ञों का शक इस बयान की सच्चाई है, हालांकि मैं नहीं कर सकते हैं अन्यथा साबित होते हैं.

Riemann परिकल्पना

जब तक 1859 वहाँ का पता नहीं था किसी भी regularities जो वर्णन होगा कि कैसे प्रधानमंत्री की संख्या के बीच वितरित कर रहे हैं । शायद यह था कि इस तथ्य के कारण किया गया था विज्ञान में लगे हुए अन्य मायने रखती है । हालांकि, मध्य 19 वीं सदी में स्थिति बदल गया है, और वे में से एक बन गया सबसे अधिक प्रासंगिक है, जो शुरू में संलग्न करने के लिए गणित.

Riemann परिकल्पना में उभरा इस अवधि — इस धारणा है कि वितरण के प्रधानमंत्री की संख्या है, वहाँ एक निश्चित पैटर्न है ।

आज, कई आधुनिक विद्वानों का मानना है कि अगर यह साबित कर दिया है, हम होगा पर पुनर्विचार करने के लिए कई मौलिक सिद्धांतों के आधुनिक क्रिप्टोग्राफी, रीढ़ की हड्डी का एक महत्वपूर्ण हिस्सा ई-कॉमर्स के.

के अनुसार Riemann परिकल्पना है, प्रकृति के वितरण के प्रधानमंत्री की संख्या, शायद काफी से अलग करना । तथ्य यह है कि अप करने के लिए अब है नहीं किया गया है अभी तक की खोज की किसी भी प्रणाली के वितरण में प्रधानमंत्री की संख्या. उदाहरण के लिए, वहाँ है इस समस्या का ‘जुड़वां”, के बीच अंतर जो 2 के बराबर है. इन नंबरों कर रहे हैं, 11 और 13, 29. अन्य प्रधानमंत्री की संख्या के फार्म समूहों. यह 101, 103, 107, आदि., वैज्ञानिकों ने लंबे समय से संदेह है कि इस तरह के समूहों के बीच मौजूद एक बहुत बड़ी primes. यदि आप पाते हैं उन्हें, स्थायित्व के आधुनिक क्रिप्टोग्राफिक कुंजी प्रश्न में बुलाया जाएगा.

परिकल्पना पर हॉज चक्र

यह अभी भी अनसुलझे समस्या तैयार की है में 1941. के हॉज अनुमान से पता चलता है की संभावना approximating के आकार के द्वारा किसी वस्तु में "gluing" एक साथ, सरल निकायों के उच्च आयाम है. इस विधि ज्ञात किया गया है और सफलतापूर्वक इस्तेमाल किया एक लंबे समय के लिए. लेकिन यह ज्ञात नहीं है करने के लिए किस हद तक यह संभव है करने के लिए बनाने के सरलीकरण.

अब तुम्हें पता है क्या न सुलझा हुआ समस्याओं पल में मौजूद है । वे कर रहे हैं विषय के अनुसंधान के वैज्ञानिकों के हजारों दुनिया भर में सभी. यह आशा की जाती है कि वे निकट भविष्य में हल हो जाएगा, और उनके व्यावहारिक आवेदन में मदद मिलेगी मानवता के लिए तक पहुँचने के एक नए चरण में तकनीकी विकास है.