Unlösbare Aufgabe: die Gleichungen von Navier-Stokes, die Hypothese Hoxha, die Riemann-Hypothese. Aufgaben Millenium
Unlösbare Aufgaben — es ist 7 interessante mathematische Probleme. Jeder von Ihnen angeboten wurde seinerzeit bekannten Wissenschaftlern, in der Regel in Form von Hypothesen. Seit vielen Jahrzehnten über Ihre Entscheidung den Kopf zerbrochen Mathematik auf der ganzen Welt. Diejenigen, die erfolgreich, wartet eine Belohnung von einer Million US-Dollar, angeboten vom Institut für Клэйя.
Vorgeschichte
Im Jahr 1900 wurde der große Deutsche Mathematiker-Kombi David Hilbert, stellte eine Liste von 23 Problemen.
Studien durchgeführt mit dem Ziel, Sie zu lösen, hatten einen enormen Einfluss auf die Wissenschaft des 20. Im Moment sind die meisten von Ihnen bereits nicht mehr Rätseln. In der Zahl der ungelöste oder gelöste teilweise geblieben:
- Das Problem der widerspruchslosigkeit der arithmetischen Axiome;
- Das Allgemeine Gesetz der Gegenseitigkeit Raum auf jedem Zahlenfeld;
- Mathematische Untersuchung von physikalischen Axiome;
- Forschung quadratische Formen mit beliebigen algebraischen numerischen Koeffizienten;
- Das Problem der strengen Begründung исчислительной geometrie Fedor Schubert;
- Etc.
Unerforscht sind: das Problem der Verteilung auf eine beliebige rechteckige Bereich der Rationalität der bekannten Theorem Кронекера und die Riemann-Hypothese.
Institut für Клэйя
Unter diesem Namen bekannt ist eine private non-Profit-Organisation, mit Hauptsitz in Cambridge, Massachusetts. Sie wurde 1998 gegründet Harvard Mathematiker A. jeffy und Geschäftsmann L. Клэйем. Ziel des Instituts ist die Förderung und Entwicklung mathematischen Wissens. Um es zu erreichen Organisation Award gibt Wissenschaftler und fördert vielversprechende Forschung.
Mehr:
Das Deutsche Flugzeug "Messerschmitt-262": die Geschichte der Entstehung, Merkmale, Foto
High-Speed-Strahltriebwerk-Kämpfer-Abfangjäger Messerschmitt ME-262 Schwalbe („Messerschmitt ME-262 Schwalbe») erschien auf dem Schlachtfeld nur im Jahr 1944. Man kann nicht genau sagen, für welchen Job diese Maschine bestimmt. Experiment...
Moderne Schule: Geschichte, Voraussetzungen, Probleme. Modelle der modernen Schulen
Historische Entstehung von Schulen förderte den Wunsch der Menschen die Welt zu erkennen und erweitern Ihre Kenntnisse. Deshalb versucht der Mensch zur Gemeinschaft mit den weisen und sehnte sich danach von Ihnen zu lernen wissen.die Geschichte der m...
"Haare zu Berge": Bedeutung, Herkunft фразеологизма
In der Russischen Sprache treffen eine ausreichende Anzahl von geheimnisvollen Floskeln, über deren Bedeutung schwer zu erraten. Die sprachliche Konstruktion „die Haare» gehört eindeutig zu den solchen. Zum Glück, der Ursprung dieses Ausd...
Am Anfang des 21 Jahrhunderts Mathematische Institut Клэйя vorgeschlagen, eine Prämie für diejenigen, die Probleme löst, die bekannt sind, wie die komplexe unlösbare Aufgaben, indem Sie Ihre Liste der Millennium Prize Problems. Aus „Liste Hilbert» in ihm kam nur die Riemann-Hypothese.
Aufgaben Millenium
In die Liste des Instituts für Клэйя ursprünglich gehörten:
- Hypothese über die Zyklen der Hodscha;
- Die Gleichungen der Quantentheorie Young ä Mills;
- Poincare-Hypothese;
- Das Problem der Gleichheit der Klassen P und NP;
- Die Riemann-Hypothese;
- Gleichungen von Navier Stokes, über die Existenz und Glattheit seiner Entscheidungen;
- Das Problem Birch Society ä Свиннертон-Dyer.
Diese offene mathematische Probleme, von großem Interesse, da möglicherweise viele praktische Implementierungen.
Was Grigori Perelman bewiesen
Im Jahr 1900 wurde der berühmte Wissenschaftler und Philosoph Henri Poincaré vermutete, dass jede односвязное kompakte 3-dimensionale Mannigfaltigkeit ohne Rand гомеоморфно 3-dimensionalen Bereich. Ihr Beweis im Allgemeinen Fall befand sich nicht im Laufe des Jahrhunderts. Nur in den Jahren 2002-2003 Petersburger Mathematiker G. Perelman veröffentlichte eine Reihe von Artikeln mit der Lösung des Problems Poincare. Sie erzeugt den Effekt der zerrissenen Bombe. Im Jahr 2010 Poincare-Hypothese wurde ausgeschlossen aus der Liste der „Ungelöste Aufgaben» Institut für Клэйя, und die meisten Перельману wurde vorgeschlagen, ihm die gebührende preiswert ist, von denen die letztere weigerte sich, nicht erklärt die Gründe für Ihre Entscheidung.
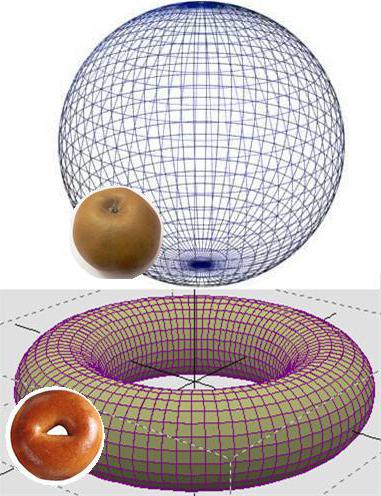
Die verständliche Erklärung, was zu beweisen in der Russischen und der Mathematik gegeben werden kann, sich vorzustellen, dass auf Donut (Torus), spannen die Gummischeibe und dann abziehen versuchen die Kanten eines Kreises in einem Punkt. Es ist offensichtlich, dass es unmöglich ist. Eine andere Sache, möchten Sie dieses Experiment mit der Kugel. In diesem Fall scheint die dreidimensionale Sphäre, die resultierende aus dem Laufwerk, dessen Umfang in zusammengerissen hypothetischen Punkt der Schnur, wird im dreidimensionalen Sinne eines gewöhnlichen Menschen, sondern zweidimensional in Bezug auf Mathematik.
Poincaré spekuliert, dass die dreidimensionale Sphäre ist die einzige dreidimensionale „Gegenstand», deren Oberfläche kann man abziehen in einem Punkt, und Перельману geschafft, es zu beweisen. Also, die Liste der „Unlösbare Aufgaben» heute besteht aus 6 Probleme.

Die Theorie von Yang-Mills
Dieses mathematische Problem vorgeschlagen wurde Sie von den Autoren aus dem Jahr 1954. Die wissenschaftliche Formulierung der Theorie ist folgender: für jede einfache kompakte Kalibrierung der Gruppe Quanten-räumliche Theorie, erstellt von Young-und Милльсом, existiert, und hat dabei null-Fehler-Masse.
Wenn man in der Sprache verständlich für den normalen Menschen, die Interaktion zwischen natürlichen Objekten (Partikeln, Körpern, Wellen, etc.) teilen sich in 4 Typen: elektromagnetische, Gravitations -, schwache und starke. Schon viele Jahre Physik versuchen, eine Allgemeine Theorie der Felder. Es muss ein Instrument zur Erklärung aller dieser Wechselwirkungen. Die Theorie von Yang-Mills ä diese mathematische Sprache, durch die es möglich beschreiben 3 der 4 Grundkräfte der Natur. Sie gilt nicht für die Gravitation. Man kann also nicht davon ausgehen, dass Young und Миллсу gelungen, eine Theorie des Feldes.
Außerdem Nichtlinearität vorgeschlagenen Gleichungen macht Sie extrem schwierig zu lösen. Bei kleinen Konstanten Zusammenhang kann Sie näherungsweise zu lösen, als eine Reihe von Theorien Störungen. Es ist jedoch unklar, wie diese Gleichungen kann gelöst werden, wenn eine starke Verbindung.

Gleichungen von Navier-Stokes
Mit Hilfe dieser Ausdrücke beschreibt solche Prozesse, wie Luftströmung, für Flüssigkeiten und Turbulenzen. Für einige private Anlässeanalytische Lösung der Gleichungen von Navier-Stokes-Gleichungen wurden bereits gefunden, allerdings ist es für die Allgemeine noch niemandem gelungen. Zur gleichen Zeit, numerische Simulationen für bestimmte Werte von Geschwindigkeit, Dichte, Druck, Zeit und so weiter ermöglicht hervorragende Ergebnisse erzielen. Es ist zu hoffen, dass bei jemandem klappt anwenden Gleichungen Navier-Stokes-Gleichungen in umgekehrter Richtung, d.h. berechnen mit Ihrer Hilfe die Parameter, oder um zu beweisen, dass die Methode keine Lösung.
Aufgabe Birch Society ä Свиннертон-Dyer
Zur Kategorie „Ungelöste Aufgaben» gilt die Hypothese, vorgeschlagen von britischen Wissenschaftlern von der University of Cambridge. Noch vor 2300 Jahren altgriechisch Wissenschaftler ewklid eine vollständige Beschreibung der Lösungen der Gleichung x2 + y2 = z2.
Wenn für jede der Primzahlen Anzahl der Punkte auf der Kurve an seinem Modul, erhalten Sie eine unendliche Anzahl von ganzen zahlen. Wenn in konkreter Weise „kleben“ seine in 1 Funktion einer komplexen Variable, dann ergibt sich das Zeta-Funktion hasse-weil für die Kurve Dritter Ordnung, gekennzeichnet durch den Buchstaben L. Es enthält Informationen über das Verhalten der modulo aller Primzahlen ein.
Brian Birch und Peter Свиннертон-Dyer stellen die Hypothese bezüglich der elliptischen Kurven. Nach Ihr, die Struktur und die Anzahl der Menge von rationalen Entscheidungen verbunden mit dem Verhalten von L-Funktionen in einer Einheit. Die unbewiesene im Moment Hypothese Birch Society ä Свиннертон-Dyer abhängig Beschreibungen von algebraischen Gleichungen 3. Grades und ist die einzige relativ einfache Allgemeine Weise die Berechnung des Grades der elliptischen Kurven.
Zu verstehen, die praktische Bedeutung dieser Aufgabe, es genügt zu sagen, dass in der modernen Kryptographie auf elliptischen Kurven basiert eine ganze Klasse von asymmetrischen Systemen, und auf deren Anwendung basieren die heimischen Standards für die digitale Signatur.

Die Gleichheit der Klassen p und np
Wenn die anderen „Aufgaben Millenium» beziehen sich auf die rein mathematischen, diese ist relevant für die aktuelle Theorie der algorithmen. Das Problem bezüglich der Gleichheit der Klassen P und np, bekannt auch als das Problem der Cook-Levin, verständlichen Sprache kann wie folgt formuliert werden. Nehmen wir an, dass eine positive Antwort auf eine Frage kann man überprüfen ausreichend schnell, D. H. für полиномиальное Zeit (PT). Dann ob die Behauptung, dass die Antwort darauf kann sehr schnell zu finden? Noch einfacher wird diese Aufgabe klingt so: ob die Lösung des Problems zu überprüfen ist nicht schwieriger, als es zu finden? Wenn die Gleichheit der Klassen P und np wird jemals bewiesen, das alle Probleme der Auswahl können Sie entscheiden, für Zuluft. Im Moment viele Experten zweifeln am Wahrheitsgehalt dieser Behauptung, obwohl das Gegenteil nicht beweisen können.

Die Riemann-Hypothese
Bis 1859 gab es keine irgendwelche Gesetzmäßigkeiten, die beschreiben würde, wie sind die Primzahlen unter den natürlichen. Vielleicht war dies aufgrund der Tatsache, dass die Wissenschaft beschäftigte sich mit anderen Fragen. Doch zur Mitte des 19 Jahrhunderts hat sich die Situation geändert, und Sie wurde zu einem der dringendsten, die begann mit Mathe.
Die Riemann-Hypothese, die in dieser Zeit " ist die Annahme, dass in der Verteilung der Primzahlen gibt es eine gewisse Regelmäßigkeit.
Heute viele moderne Wissenschaftler glauben, dass wenn es bewiesen wird, dann müssen überdacht werden viele grundlegende Prinzipien der modernen Kryptographie, die die Grundlage des großen Teils der E-Commerce-Mechanismen.
Nach der Hypothese von Riemann, das die Verteilung der Primzahlen, vielleicht unterscheidet sich deutlich von der angeblichen im Moment. Die Tatsache, dass bis jetzt noch nicht erkannt wurde irgendwelche Systeme in der Verteilung der Primzahlen. Zum Beispiel gibt es das Problem „Twins», die Differenz zwischen denen gleich 2. Diese zahlen sind 11 und 13, 29. Andere Primzahlen Cluster zu bilden. Es ist 101, 103, 107 und andere Wissenschaftler haben lange vermutet, dass solche Ansammlungen gibt es auch unter sehr großen Primzahlen. Wenn Ihr Sie findet, dann ist die Haltbarkeit der modernen криптоключей in Frage gestellt werden.

Hypothese über die Zyklen der Hoca
Diese bisher ungelöstes Aufgabe formuliert im Jahr 1941. Hypothese Hoxha beinhaltet die Möglichkeit der approximation der Form eines Objekts durch „kleben“ zusammen einfachen Körpern größerer Dimension. Diese Methode war bekannt und seit langem erfolgreich angewendet. Es ist jedoch nicht bekannt, inwieweit können Sie produzieren eine Vereinfachung.
Jetzt wissen Sie, welche unlösbare Aufgaben gibt es im Moment. Sie sind Gegenstand der Forschung von tausenden von Wissenschaftlern aus der ganzen Welt. Es bleibt zu hoffen, dass Sie bald gelöst werden, und Ihre praktische Anwendung Menschheit helfen, sich auf eine neue Runde der technologischen Entwicklung.
Article in other languages:
AR: https://tostpost.com/ar/education/1204-navier.html
HI: https://tostpost.com/hi/education/1204-navier--riemann.html
JA: https://tostpost.com/ja/education/1203-navier-stokes-hodge.html

Alin Trodden - autor des Artikels, Herausgeber
"Hi, ich bin Alin Trodden. Ich schreibe Texte, lese Bücher und suche nach Eindrücken. Und ich bin nicht schlecht darin, dir davon zu erzählen. Ich freue mich immer, an interessanten Projekten teilzunehmen."
Verwandte News
Russische Hochschulen architektonische: Bewertung, Beschreibung, Merkmale und Bewertungen
Entwicklung von Engineering-Plänen und Zeichnungen, Umsetzung der ehrgeizigen Bauvorhaben, Neugestaltung des erzeugten Objekts und übergabe ihn dem Kunden – alles ist der Bereich der beruflichen Tätigkeit von Architekten. In...
Die Struktur der Eizelle: Allgemeine Informationen
Ei ä diese sexuelle Käfig des Weibchens, die in sich selbst гаплоидный Satz von Chromosomen. Ihre Hauptvorausbestimmung ä übertragung der genetischen Information während der Befruchtung. Die Struktur der Eizelle in der N...
Immobilien-repräsentative Monarchie als eine Form der staatlichen Verwaltung
die Monarchie gehört zu den ältesten Formen der Regierung. Ihre Besonderheit liegt darin, dass die Herrschaft über alle Sphären des Staates gehört einer einzigen Person auf das Recht престолонаследования. In der Antike glaubte man...
Eine umfassende Analyse. Beschreibung
Analyse der wirtschaftlichen ttigkeit – es ist ein System von Techniken entwickelt, die wissenschaftliche Methode, Dank dem wird vielleicht das Studium der Betriebswirtschaftslehre. Mit Ihrem Einsatz zeigen sich die Produkti...
Trägheitsmoment. Einige Details der mechanik Starrer Körper
Eines der grundlegenden physikalischen Prinzipien der Wechselwirkung von Festkörpern ist das Gesetz der Trägheit, formuliert noch der große Isaac Newton. Mit diesem Begriff begegnen wir fast ständig, da es einen extrem großen Einf...
1147 Jahr - was ist das Jahrhundert für die Bildung von Moskau?
„der Pantheon der Russischen Zaren» enthält Informationen darüber, dass die ersten Stämme auf dem Territorium des heutigen Moskau beherrscht das Land noch in der 880-m zum Jahr. Viele Wissenschaftler stellen sich die F...






















Kommentare (0)
Dieser Artikel wurde noch kein Kommentar abgegeben, sei der erste!