Now - 15:12:27
معادلة الطائرة: كيف اصنع ؟ أنواع المعادلات من الطائرة
الفضاء الطائرة يمكن تعيين بطرق مختلفة (نقطة واحدة و ناقلات نقطتين و ناقلات ثلاث نقاط ، إلخ.). مع هذا في الاعتبار, معادلة طائرة مختلفة الأنواع. كما تخضع لشروط معينة ، الطائرة يمكن أن تكون موازية, عمودي, المتقاطعة ، إلخ. والحديث عن هذا في هذه المقالة. سوف نتعلم كيفية الحصول على المعادلة العامة من الطائرة.
عادي المعادلات
على سبيل المثال ، هناك مساحة R3 التي مستطيل تنسيق نظام XYZ. تعريف ناقلات &ألفا;, الذي سيصدر من النقطة الأولي س خلال نهاية ناقلات &ألفا; رسم طائرة P الذي هو عمودي على.
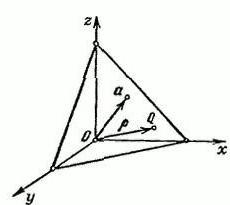
للدلالة P التعسفي نقطة Q=(x,y,z). نصف قطر ناقل من النقطة س التوقيع على رسالة R. طول ناقلات &ألفا; يساوي R=I&ألفا;أنا و Ʋʋ=(cos&ألفا; لأن&بيتا; لأن&غاما;).
هذا هو وحدة متجه التي يتم توجيهها في اتجاه متجه &ألفا;. &ألفا;, &بيتا; و &غاما; – زوايا شكلت بين ناقلات Ʋʋ و اتجاهات إيجابية من محاور الفضاء x, y, z, على التوالي. الإسقاط في أي نقطة على QϵП Ʋʋ ناقلات هو ثابت ، والتي تساوي R: (ف ، Ʋʋ) = p(p≥0).
المحدد المعادلة المنطقي عند R=0. الطائرة الوحيدة P في هذه الحالة سوف عبور نقطة (&ألفا;=0), وهو الأصل, و وحدة متجه Ʋʋ أطلقت من نقطة O عمودي على الصفحة ، على الرغم من اتجاه ، وهو ما يعني أن Ʋʋ ناقلات يتم تحديد ما يصل الى علامة. السابقة المعادلة هي معادلة طائرتنا P يتم التعبير عنها في شكل ناقل. ولكن في الإحداثيات أنها سوف تبدو مثل هذا:
المزيد
أساليب التدريس التفاعلية في جامعة
أساليب التدريس التفاعلية هي واحدة من أهم وسائل تحسين التدريب المهني من الطلاب في التعليم العالي. المعلم هو الآن لا يكفي أن تكون ببساطة المختصة في الانضباط ، وإعطاء المعرفة النظرية في الفصول الدراسية. تحتاج بعض نهج مختلف الحديثة في العملية التعليمية.ن...
البرازيل الذي أعداد السكان في المرتبة الخامسة المرتبة الثانية بعد الهند والصين وإندونيسيا وأمريكا – متنوعة جدا البلد. لعدة مئات من السنين الأمة أصبح من أهم العرقية-الثقافية والتعليم. سكان البرازيل هو أكثر من مائة القوميات والشعوب. في هذا ...
مستعمرة من بريطانيا – العديد من المناطق في جميع أنحاء العالم ، الذين تم القبض عليهم ، تؤخذ تحت الحماية أو بعض الوسائل المكتسبة بين 16 و 18 قرون واحدة من أقوى الإمبراطوريات في الماضي – البريطانية. وكان الهدف من التنمية الإقليمية. خلال الفت...
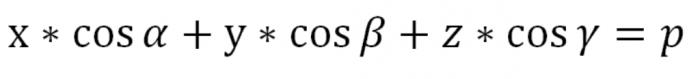
هنا, R أكبر من أو يساوي 0. وجدنا المعادلة من طائرة في الفضاء في شكل طبيعي.
عام المعادلات
إذا المعادلة في الإحداثيات ضرب من قبل أي رقم غير الصفر, سوف نحصل على المعادلة ، وهذا هو ما يعادل تحديد نفس الطائرة. سوف تبدو مثل هذا:
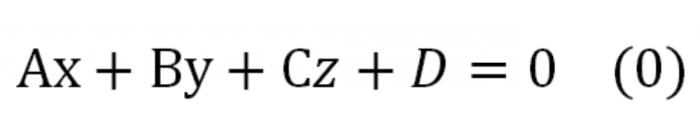
هنا A, b, C – هذا هو عدد في وقت واحد يختلف عن الصفر. هذه المعادلة يشار إلى معادلة طائرة الشكل العام.
المعادلات من الطائرات. حالات خاصة
المعادلة في شكل عام يمكن تعديلها مع شروط إضافية. النظر في بعض منها.
أعتقد أن معامل يساوي 0. وهذا يعني أن تعطى الطائرة موازية على المحور ox. في هذه الحالة, المعادلة سوف تتغير: vu+Cz+D=0.
كما أن المعادلة سوف تتغير وفقا للشروط التالية:
- إذا=0 ثم المعادلة سوف تتغير إلى ax+Cz+D=0, التي من شأنها أن تشير إلى مواز إلى المحور Oy.
- ثانيا ، إذا ج=0 المعادلة يتم تحويلها إلى أوه+وو+D=0, والتي سوف أتكلم عن مواز إلى المحور Oz.
- ثالثا ، إذا كان D=0 المعادلة تبدو ax+وو+Cz=0 ، مما يعني أن الطائرة يتقاطع O (أصل الإحداثيات).
- الرابعة ، إذا كان A=B=0 المعادلة سوف تتغير إلى Cz+D=0, والتي سوف تثبت ذلك أوكسي.
- الخامسة ، إذا كان B=C=0 المعادلة يصبح ax+D=0 و هذا يعني أن الطائرة موازية Oyz.
- السادسة ، إذا كان A=C=0 المعادلة سوف تأخذ شكل vu+D=0 هذا هو تقرير مواز Oxz.
شكل المعادلة في قطاعات
في حالة الأعداد A ، b ، C ، D هي غير صفرية المعادلة (0) يمكن أن تكون على النحو التالي:
س/أ + ص/ب + z/C = 1
فيه = D/A, b = -D/ C = D/س.
الناتجة المعادلة الطائرة في شرائح. وتجدر الإشارة إلى أن هذه الطائرة سوف عبور المحور ox عند النقطة ذات الإحداثيات (a,0,0), Oh – (0,b,0) أوقية – (0,0,ج).
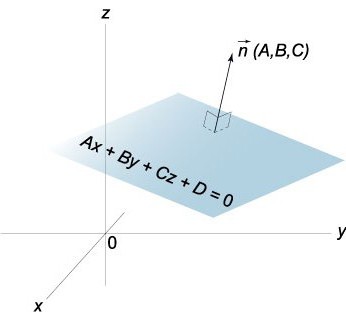
بالنظر إلى المعادلة س/أ + ص/ب + z/C = 1 فمن السهل تصور موقع الطائرة بالنسبة إلى تعريف نظام الإحداثيات.
إحداثيات العادي ناقلات
عادي ناقلات ن أن الطائرة P الإحداثيات التي معاملات المعادلة العامة من هذه الطائرة ، أي أن ن (أ ، ب ، ج).
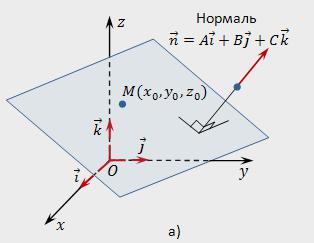
لتحديد إحداثيات طبيعي n, يكفي أن تعرف المعادلة العامة من إعطاء الطائرة.
عند استخدام المعادلة في القطاعات التي لديها شكل س/أ + ص/ب + z/C = 1 كما في المعادلة العامة ، يمكننا كتابة إحداثيات أي متجه طبيعي معين الطائرة: (1/أ + 1/ب + 1/ج).
ومن الجدير بالذكر أن متجه طبيعي يساعد على حل مجموعة متنوعة من المشاكل. الأكثر شيوعا هي الهدف دليل على تعامد أو التوازي الأسطح, مهمة إيجاد الزوايا بين الطائرات أو الزوايا بين الطائرات وخطوط مستقيمة.
شكل المعادلة الطائرة وفقا إحداثيات نقطة العادي ناقلات
غير صفرية ناقلات ن عمودي على تحديد الطائرة التي تسمى normal (عادي) نظرا الطائرة.
أعتقد أن في تنسيق الفضاء (مستطيلة تنسيق النظام) Oxyz المحدد:
- نقطة مو مع الإحداثيات (xₒ,yₒ,zₒ) ؛
- صفر ناقلات n=A*i+A*j+ج*ك.
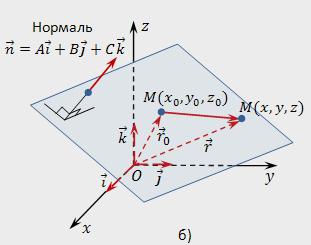
نحن بحاجة إلى كتابة المعادلة الطائرة التي سوف تمر من خلال نقطة مو هو عمودي على العادي n.
في الفضاء نختار أي التعسفي نقطة تدل على أنه M (x,z). السماحنصف قطر ناقل من أي نقطة M (x,y,z) r=x*y*ي+z*ك و نصف قطرها-متجه من نقطة مو (xₒ,yₒ,zₒ) – rₒ=xₒ*أنا+yₒ*ي+zₒ*ك. النقطة M تنتمي إلى المحدد الطائرة ، إذا كان متجه من المنظمة الدولية للهجرة سوف يكون عمودي على متجه n. الكتابة حالة التعامد باستخدام دوت المنتج:
[المنظمة الدولية للهجرة ، n] = 0.
منذ MΩ = r– rₒ, ناقلات معادلة الطائرة سوف تبدو مثل هذا:
[r-rₒ ، n] = 0.
هذه المعادلة قد تكون مختلفة الشكل. لهذا الغرض ، خصائص المنتج العددية ، يتم تحويلها إلى الجانب الأيسر من المعادلة. [ص-rₒ ، n] = [r, n] و [ندش] ؛ [rₒ ، n]. إذا [rₒ ، n] للدلالة ج ، نحصل على المعادلة التالية: [r, n] - C = 0 أو [r, n] = C الذي يعبر عن ثبات التوقعات على العادي ناقلات قطر-نواقل معينة النقاط التي تنتمي إلى الطائرة.
من الممكن الآن إلى تنسيق قياسي ناقل المعادلة من الطائرة لدينا [r-rₒ ، n] = 0. منذ r–rₒ = (x–xₒ)*أنا + (–yₒ)*j + (z-zₒ)*k و n = A*i+A*j+ج*ك ، لدينا:
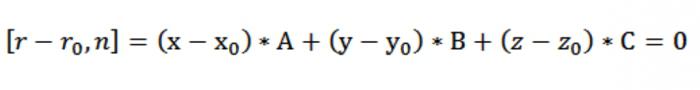
لذلك ، لقد شكلت معادلة الطائرة يمر من خلال نقطة عمودي طبيعي n:
*(x - xₒ)+*(– yₒ)*(z-zₒ)=0.
شكل المعادلة الطائرة وفقا إحداثيات نقطتين و ناقلات ، متداخلة إلى الطائرة
نحدد اثنين التعسفي نقطة M′ (x′,′ z′) M″ (x″,″ z″) المتجه a (a′ و″ ، و").
الآن يمكننا كتابة المعادلة من معين الطائرة التي سوف تمر من خلال نقطة M′ M″ ، أي نقطة M مع الإحداثيات (x,y,z) موازية محدد ناقلات.
ناقلات في M′M={x-x′ t′;z′} M″M={x″ x′;u″-y′ z″ z′} يجب أن يكون متحد المستوى مع المتجه a=(a′ و″ ، و") ، والتي تعني (M′M″م ، أ)=0.
لذلك لدينا المعادلة من الطائرة في الفضاء سوف تبدو مثل هذا:
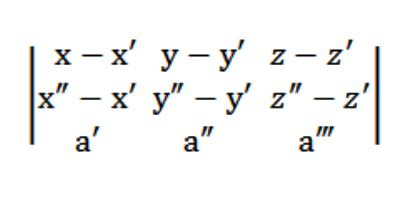
شكل معادلة الطائرة التي يتقاطع ثلاث نقاط
لنفترض أن لدينا ثلاث نقاط: (x′,′,z′), (x″,″ z″), (x","y,z") التي لا تنتمي إلى خط مستقيم واحد. يجب أن تكتب المعادلة الطائرة يمر من خلال تحديد النقاط الثلاث. نظرية الهندسة يؤكد أن هذه الطائرة لا وجود لها إلا إنها واحدة فقط. منذ هذه الطائرة يتقاطع النقطة (x′,′ z′) المعادلة على النحو التالي:
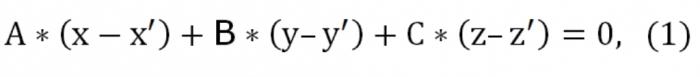
هنا أ ، ب ، ج مختلفة من الصفر في نفس الوقت. أيضا بالنظر إلى الطائرة يتقاطع نقطتين: (x″,″ z″) و (x","y,z"). في هذا الصدد يجب أن يتم تنفيذ مثل هذه الظروف:
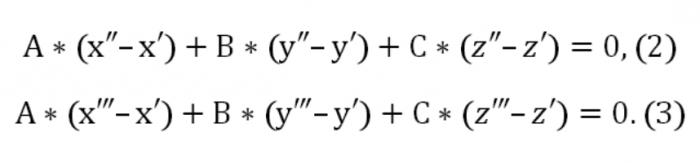
الآن يمكننا كتابة متجانسة نظام من المعادلات (الخطية) مع المجهول u, v, w:
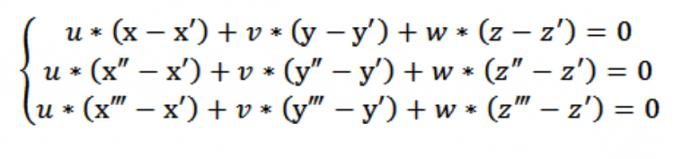
في حالة x,y أو z الأعمال التعسفية نقطة يرضي المعادلة (1). بالنظر إلى المعادلة (1) و نظام المعادلات (2) و (3) نظام المعادلات هو موضح في الشكل أعلاه ، يفي ناقلات N (A,b,C), وهو غير تافهة. وذلك لأن العامل المحدد لهذا النظام تساوي صفر.
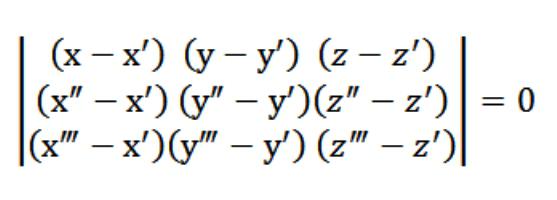
المعادلة (1), وهذا ما فعلناه, هذه هي المعادلة الطائرة. 3 نقطة بالتأكيد, وأنه من السهل أن تحقق. لهذا تحتاج إلى وضع مفاتيح لدينا عناصر في الصف الأول. من القائمة خصائص المحددات ويترتب على ذلك أن لدينا طائرة في وقت واحد يتقاطع ثلاثة أصلا معين من النقاط (x′,′ z′), (x″,″ z″), (x","y,z"). لذلك قررنا مجموعة مهمة قبل.
ثنائي السطح الزاوية بين الطائرات
ثنائي السطح زاوية المكاني الشكل الهندسي شكلت من قبل اثنين من نصف الطائرات التي تنشأ من نفس الخط. وبعبارة أخرى, هذا جزء من المساحة التي تقتصر هذه نصف الطائرات.
لنفترض أن لدينا طائرتين مع المعادلات التالية:
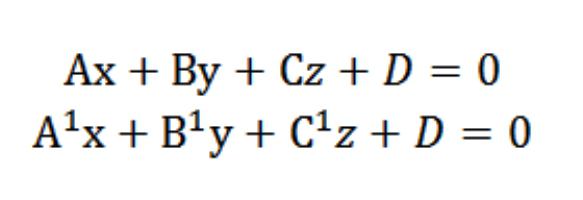
ونحن نعلم أن ناقلات ن=(أ ، ب ، ج) و N¹=(A¹¹,¹) عمودي وفقا المحدد الطائرات. في هذا الصدد, زاوية &phi بين ناقلات N و N¹ تساوي زاوية (ثنائي السطح) الذي يقع بين هذه الطائرات. Scalar product وقد شكل:
NN¹=|N||N¹|cos φ
كوس و فاي;= NN¹/|N||N¹|=(a¹+W¹+SS¹)/((√(A²+B²+S²))*(√(A¹)²+(V¹)²+(S¹)²)).
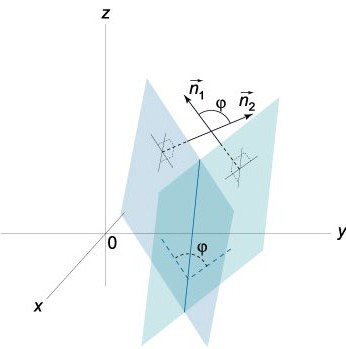
يكفي أن نلاحظ أن 0≤φ≤π.
في الواقع اثنين من الطائرات التي تتقاطع على شكل زاويتين (ثنائي السطح): و فاي;1 و فاي;2. مجموع منهم يساوي π (φ1+ و فاي;2= π). كما عن التمام ، القيم المطلقة متساوية ، ولكنها تختلف في علامات, هو, لأنه و فاي;1=-جتا و فاي;2. إذا المعادلة (0) إلى استبدال A ، b و C أعداد A-b -C ، على التوالي ، ثم المعادلة التي نحصل عليها ستحدد نفس الطائرة, فقط زاوية و فاي; في المعادلة كوس و فاي;= NN1/|N||N1| سيتم استبدال π-φ.
معادلة عمودي على الطائرة
دعا عمودي الطائرة بينهما زاوية 90 درجة. باستخدام المواد المقدمة أعلاه, يمكن أن نجد معادلة طائرةعمودي على الآخر. دعونا نقول لدينا طائرتين: ax+وو+Cz+D=0¹x¹+¹z+D=0. نستطيع أن نقول أنها سوف يكون عمودي إذا كوس و فاي;=0. وهذا يعني أن NN¹=AA¹+BB¹+SS¹=0.
معادلة موازية الطائرة
يشار إلى اثنين من موازية الطائرات التي لا تحتوي على نقاط مشتركة.
حالة التوازي من طائرات (المعادلات هي نفسها كما في الفقرة السابقة) هو أن ناقلات N و N¹ أنها هي عمودي على خط واحد. وهذا يعني أن الشروط التالية التناسب:
A/A¹=/¹=/¹.
إذا كانت الشروط التناسب تمتد إلى A/A¹=/¹=/¹=DD¹
وهذا يدل على أن البيانات الطائرة هي نفسها. هذا يعني أن المعادلة ax+وو+Cz+D=0¹x¹+¹z+D¹=0 لوصف نفس الطائرة.
المسافة إلى الطائرة من نقطة
لنفترض أن لدينا طائرة P والتي تعطى من المعادلة (0). تحتاج إلى العثور على المسافة بين نقطة مع الإحداثيات (xₒ,yₒ,zₒ)=Qₒ. للقيام بذلك, تحتاج إلى إعطاء معادلة الطائرة P في شكل طبيعي:
(&رو; v)=p (p≥0).
في هذه الحالة &رو; (x,y,z) هو نصف قطر ناقل من وجهة نظرنا س يقع في P, R & ndash; هو طول عمودي P, الذي صدر من نقطة الصفر, v – هو وحدة متجه في اتجاه.
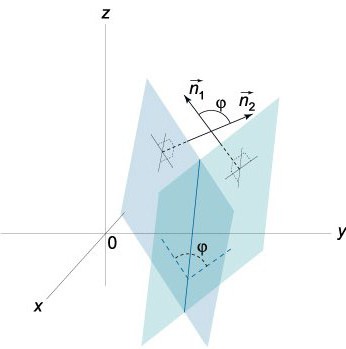
&رو;-&رو;º نصف قطر ناقل من أي نقطة Q=(x,y,z) التي تنتمي إلى P ، radius-متجه من نقطة معينة Q0=(xₒ,yₒ,zₒ) مثل ناقلات, القيمة المطلقة الإسقاط الذي في الخامس يساوي المسافة d التي تحتاج إلى أن وجدت من س0=(xₒ,yₒ,zₒ) P:
=D|(&رو;-&رو;0 ، v)| لكن
(&رو;-&رو;0 ، v)= (&رو; v)–(&رو;0 ، v) =R - (و رو;0 ، v).
=d|(&رو;0 ، v)-R|.
الآن يمكنك ان ترى لحساب المسافة د من س0 إلى الطائرة P, فمن الضروري استخدام المعادلات العادي من طائرة نقل إلى الجانب الأيسر من R و الأخير هو x ، y ، z بديلا (xₒ,yₒ,zₒ).
وهكذا ، نجد القيمة المطلقة مما أدى التعبير ، د هو المطلوب.
استخدام لغة المعلمات التي تم الحصول عليها واضحة:
د=|ج+Vuo+Czₒ|/√ (²+²+C²).
إذا كان تحديد النقطة Q0 على الجانب الآخر من الطائرة P حيث الأصل ، ناقلات &رو;-&رو;0 v زاوية منفرجة ، وبالتالي:
د=-(و رو;-&رو;0 ، v)=(&رو;0,v)-R>0.
في حالة عند النقطة Q0 جنبا إلى جنب مع أصل الإحداثيات يقع في نفس الجانب من P, خلق زاوية حادة ، هي:
د=(&رو;-&رو;0 ، v)=R - (و رو;0 ، v)>0.
والنتيجة هي أنه في الحالة الأولى (&رو;0 ، v)>R في الثانية (و رو;0 ، v)<R.
المماس الطائرة و المعادلة
على الطائرة إلى السطح في ظل نقطة مº &ndash ؛ هذه هي الطائرة التي تحتوي على كل شيء ممكن الظلال إلى منحنيات رسمها من خلال هذه النقطة على سطح الأرض.
في هذا النوع من معادلة سطح F(x,y,z)=0 معادلة المماس الطائرة في الظل نقطة مº(xº,º zº) سوف تبدو مثل هذا:
FX(xº,º zº)(x - xº)+ FX(xº,º zº)(u - uº)+ FX(xº,º zº)(z-zº)=0.
إذا قمت بتحديد السطح في شكل صريح z=f (x,y), المماس الطائرة سيتم وصفها بالمعادلة التالية:
Z-zº =f(xº,º)(x - xº)+f(xº,º)(u - uº).
تقاطع طائرتين
في الفضاء ثلاثي الأبعاد هو نظام الإحداثيات (مستطيلة) Oxyz ، نظرا طائرتين P′ P″ ، التي تتقاطع و لا تتطابق. لأن أي طائرة في مستطيل تنسيق النظام, يتم تحديدها من قبل المعادلة العامة ، فإننا نفترض أن P′ P″ يتم تعريف المعادلات من A′x′y′z+D′=0″x″y″z+D″=0. في هذه الحالة لدينا طبيعي n′ (′,′,′) - الطائرة, P′ ومن الطبيعي n″ (″,″,″) - الطائرة, P″. منذ الطائرات ليست موازية و لا تتطابق ، ثم هذه النواقل ليست على خط واحد. باستخدام لغة الرياضيات ، ونحن في هذه الحالة يمكن كتابة: n′≠ n″ ↔ (′,′,′) ≠ (λ*″,λ*″,λ*″), λϵR. اسمحوا الخط المستقيم التي تقع عند تقاطع P′ P″ ، سيتم ويرمز له بالحرف a ، في هذه الحالة a = P′ &كاب; P″.
&ndash ؛ الفيديو التي تتكون من مجموعة من النقاط (المجموع) طائرات من P′ P″. وهذا يعني أن إحداثيات أي نقطة تنتمي إلى خط مستقيم و في نفس الوقت يجب أن ترضي المعادلات من A′x′y′z+D′=0″x″y″z+D″=0. لذا إحداثيات النقطة سوف يكون خاص حل نظام من المعادلات التالية:
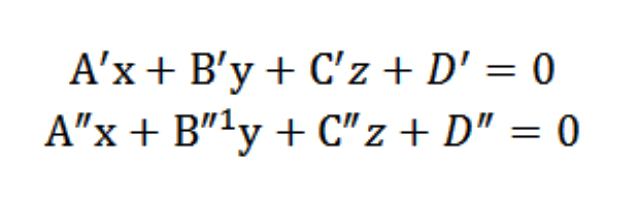
في النهاية اتضح أن الحل (المشتركة) هذا النظام من المعادلات تحديد إحداثيات كل نقطة من الخط ، والتي سوف تكون بمثابة نقطة تقاطع P′ P″ ، وتحديد الخط في نظام إحداثيات Oxyz (مستطيلة) في الفضاء.
Article in other languages:

Alin Trodden - مؤلف المقال ، محرر
"مرحبا ، أنا ألين الدوس. أنا أكتب النصوص ، وقراءة الكتب ، والبحث عن الانطباعات. وأنا لست سيئة في أقول لك عن ذلك. أنا دائما سعيد للمشاركة في مشاريع مثيرة للاهتمام."
أخبار ذات صلة
2 كاترين: سيرة حياة الإمبراطورة. تاريخ روسيا
غامضة شخصية 2 كاترين العظمى-الإمبراطورة الروسية من أصل ألماني. معظم المقالات والأفلام هي كما هو مبين محب الخدم الكرات مراحيض فاخرة, فضلا عن العديد من المفضلة ، الذين كانت قريبة جدا.للأسف قلة من الناس يعرفون أنها كانت ذكية جدا ، ال...
للإمبراطورية الأسبانية: الوصف التاريخ و العلم
الإمبراطورية الإسبانية في أيام قوتها كانت واحدة من أكبر الدول من أي وقت مضى في العالم. إنشائها هو وثيق الصلة مع عصر الاكتشافات الجغرافية الكبرى ، عندما أصبحت القوة الاستعمارية. لعدة قرون العلم من الإمبراطورية الإسبانية تطورت على أ...
المواضيعية مجموعة من الكلمات: أمثلة
ما هي وحدة اللغة الروسية ؟ بالطبع كلمة. مع ذلك, نتواصل, حصة كل منهما الأفكار والمشاعر. تتناول المقالة الموضوعية مجموعة من الكلمات التي تصنف ثراء اللغة الروسية ، بما في ذلك الأدبية القاموس أكثر من 150 ألف الأسماء ، والأفعال والصفات...
البلد الأكثر سكانا في العالم. موناكو: حقائق مثيرة للاهتمام حول الإمارة
الإنسانية للغاية موزعة بشكل غير متساو على سطح كوكبنا. على سبيل المثال في البلد الآسيوي يمكن أن تستوعب أكثر الناس من كل قارة أستراليا. أين هي البلد الأكثر كثافة سكانية في العالم ؟ و ما يجعل الأمر مثيرا للاهتمام ؟ دعونا نواجه الأمر....
ما هو تجميد: تعريف سماته الرئيسية
نهر – انها ليست مجرد تيار التسرع من الجبال والتلال في البحار والمحيطات. انها جميلة النظام البيئي المعقد ، وهو نوع من “الهيئة", التي تتميز خصوصياته وسائط. في هذه المقالة سوف نركز على درجة حرارة الجليد نظم الأنهار.م...
لون علم النفس في الإعلان باعتباره أداة مبيعات
صناعة الإعلان في تزايد مستمر ومتطور ، ومع ذلك ، لم يتغير ، دراسة عميقة في النفس البشرية ، باعتبارها المشتري المحتمل. كيفية رسم كيفية لفت انتباه المشترين لنوع معين من السلع في سلسلة من العديد من مماثلة ؟ لون علم النفس في الإعلان هو...






















تعليقات (0)
هذه المادة قد لا تعليق أول