La ecuación de un plano: a componer? Tipos de ecuaciones de un plano
En el espacio plano se puede definir de diferentes maneras (un punto y un vector, dos puntos y un vector de tres puntos y otros). Es en este contexto, la ecuación del plano puede tener diferentes tipos. También, en determinadas condiciones, el plano pueden ser paralelos, perpendiculares, que se superponen, etc. acerca De esto y vamos a hablar en este artículo. Aprenderemos a formar la ecuación general del plano y no sólo.
Un aspecto Normal de la ecuación
Supongamos que tenemos un espacio R3, que tiene un sistema de coordenadas XYZ. Haremos un vector α, que se lanzará desde el punto de inicio de la Oe a Través del extremo del vector α realizaremos el plano P, que se le perpendicular.
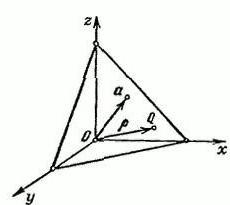
Se denota en un punto arbitrario P Q=(x,y,z). El radio-vector de un punto Q a firmar con la letra p. La longitud del vector α es igual a r=IαI y Ʋ=(cosα,cosβ,cosγ).
Este Es el único vector que apunta hacia el cómo y el vector α. α, β y γ – esto ángulos que se forman entre el vector de Ʋ y positivos direcciones de los ejes del espacio x, y, z respectivamente. Proyección de un punto en el QϵП en el vector de Ʋ es una constante, que es igual a r: (r,Ʋ) = p(p≥0).
Especificado por la ecuación tiene sentido, cuando p=0. El único, el plano P en este caso, se cruza el punto (α a=0), que es el principio de coordenadas, y un único vector de Ʋ, lanzado desde el punto De que sea perpendicular a R, a pesar de su dirección, lo que significa que el vector de Ʋ se determina con una precisión hasta de la marca. La anterior ecuación es la ecuación de nuestra plano P, expresada en forma vectorial. Y aquí están las coordenadas de su tipo será de la forma:
Más:
El general walter von Reichenau: su biografía, sus logros y la historia
El General mariscal de campo de la alemania nazi walter von Reichenau (Walter von Reichenau) se contaba entre los pocos altos oficiales del ejército de la wehrmacht, que apoyó activamente el nazismo. Durante la Segunda guerra mundial fue comandante d...
Trajes espaciales de los astronautas: de la asignación de la unidad. El primer traje espacial
Trajes espaciales de los astronautas – no es simplemente trajes de vuelo en órbita. El primero de ellos se remonta a principios del siglo veinte. Era la época de antes de los vuelos espaciales restaba casi medio siglo. Sin embargo, los científi...
Oriental de la plataforma europea: forma de alivio. Minerales oriental de la plataforma europea
La Mayor parte del territorio europeo de rusia, así como de algunos países de la cei se encuentra en la parte continental de un tramo de la corteza terrestre, que lleva el nombre oriental de la plataforma europea. La forma del relieve aquí es predomi...
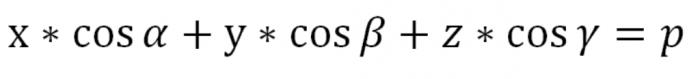
R aquí es mayor o igual a 0. Hemos encontrado la ecuación de un plano en el espacio en la vista normal.
La ecuación General
Si la ecuación en coordenadas se multiplica por cualquier número que no sea cero, obtenemos una ecuación equivalente a este, define el mismo plano. Tendrá este aspecto:
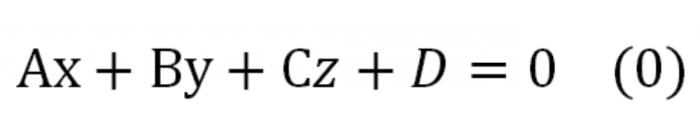
Aquí A, b, c – este número, al mismo tiempo diferente de cero. Esta ecuación se conoce como ecuación de un plano de la apariencia general.
De la Ecuación de los planos. Casos particulares
La Ecuación en forma general, puede mutar cuando hay más condiciones. Veamos algunos de ellos.
Supongamos que el coeficiente A es igual a 0. Esto significa que este plano paralelo a la especificada por el eje ox. En este caso, el tipo de la ecuación cambia: vu+Cz+D=0.
Similar a la vista de la ecuación será diferente y en las siguientes condiciones:
- En primer lugar, si A=0, la ecuación cambia a ah+Cz+D=0, lo que dará testimonio acerca de paralelas al eje de la Ue.
- En segundo lugar, si A=0, entonces la ecuación se convierte en ah+vu+D=0, que hablará sobre las paralelas a un eje Oz.
- En tercer lugar, si D=0, la ecuación se verá como ah+vu+Cz=0, lo que significaría que el plano de la cruza De (origen de coordenadas).
- En cuarto lugar, si A=B=0, entonces la ecuación cambia a Cz+D=0, que será demostrar la concurrencia de la Oxy.
- En quinto lugar, si B=C=0, entonces la ecuación sería ah+D=0, lo que significa que el plano de la Oyz paralelo.
- En sexto lugar, si A=C=0, entonces la ecuación adquiera el tipo de vu+D=0, es decir, es la de informar sobre el paralelismo de la Oxz.
Tipo de la ecuación en tramos
En el caso de que el número de A, b, c, D son diferentes de cero, el tipo de la ecuación (0) puede ser el siguiente:
X/a + y/b + z = 1,
En la que: a = -D/A, b = -D/A, c = -D/S.
Obtener como resultado la ecuación de un plano en trozos. Vale la pena señalar que este plano se cruza el eje ox en el punto con coordenadas (a,0,0), Ue – (0,b,0) y Oz – (0,0,c).
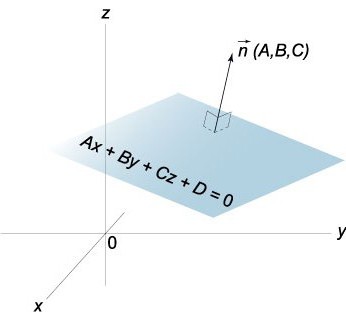
Teniendo en cuenta la ecuación x/a + y/b + z = 1 es fácil de representar visualmente el alojamiento el plano de la relación especificada de un sistema de coordenadas.
Las Coordenadas del vector normal
Vector Normal n al plano P tiene coordenadas, que son los coeficientes de la ecuación general de este plano, es decir, n (A,b,c).
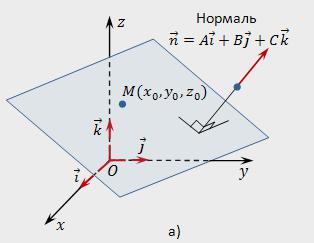
Para determinar las coordenadas de la normal n, basta con saber el total de la ecuación dada en el plano.
Cuando se utiliza la ecuación en trozos, que tiene el aspecto de x/a + y/b + z = 1, como el uso de la ecuación general, se pueden introducir las coordenadas de cualquier normal del vector especificada plano: (1/a + 1/b + 1/c).
Vale la pena señalar que el vector normal ayuda a resolver una variedad de tareas. La más común son las tareas, consistentes en la prueba de escuadras o paralelismo de los planos, la tarea de encontrar los ángulos entre los planos o de los ángulos entre los planos y rectas.
Tipo de la ecuación de un plano de acuerdo a las coordenadas de un punto y el vector normal
Un vector de n, perpendicular determinado plano, se llama normal (normal) para un determinado plano.
Supongamos que muestra el espacio de coordenadas (rectangular con un sistema de coordenadas) Oxyz se establecen:
- Punto de Мₒ con coordenadas (хₒ,уₒ,zₒ);
- El vector cero n=A*i+*+j*k.
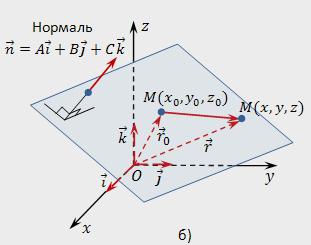
Para hacer una ecuación del plano que se llevará a cabo a través de un punto Мₒ perpendicular a la normal n.
En el espacio a elegir cualquiera de un punto arbitrario y se denota su M (x,z). Sueltael radio-vector de toda el punto M (x,y,z) será r=x*i+*j+z*k, y el radio-vector de punto de Мₒ (хₒ,уₒ,zₒ) – rₒ=хₒ*i+уₒ*j+zₒ*k. El punto M es pertenecer a determinado plano, si el vector de МₒМ será perpendicular al vector n. Anote la condición de ортогональности con la ayuda de escalar de la obra:
[МₒМ, n] = 0.
Debido a que МₒМ = r–rₒ, la ecuación vectorial del plano podría verse así:
[r – rₒ, n] = 0.
Esta ecuación puede tener una forma diferente. Para ello, se utilizan las propiedades de un valor escalar de la obra, se convierte en el lado izquierdo de la ecuación. [r – rₒ, n] = [r, n] ¡ [rₒ, n]. Si [rₒ, n] indicar como se obtiene la siguiente ecuación: [r, n] ¡ c = 0 o [r, n] = con, que expresa la consistencia de las proyecciones normal, el radio vector-vectores de puntos que pertenecen a un plano.
Ahora puede obtener dimensional tipo de registro ecuación vectorial de nuestro plano [r – rₒ, n] = 0. Dado que el r–rₒ = (x–хₒ)*i + (–уₒ)*j + (z–zₒ)*k, y n = A*i+*+j*k, tenemos:
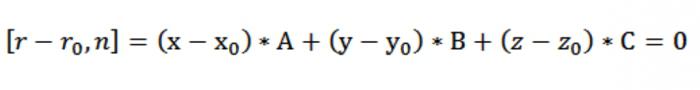
Entra, tenemos que se desarrolla la ecuación del plano que pasa a través de un punto perpendicular a la normal n:
A*(x - хₒ)+*(– уₒ)*(z–zₒ)=0.
Tipo de la ecuación de un plano de acuerdo a las coordenadas de dos puntos y un vector, коллинеарного plano
Haremos dos arbitrarias de los puntos M′ (x′,el′,z′) y M″ (x″,el″,z″), así como el vector a (a′,y″ y").
Ahora podemos componer la ecuación dada plano, que se llevará a cabo a través de los puntos M′ y M″ así como toda el punto M con coordenadas (x,y,z) en paralelo especificado por el vector y.
Cuando este vectores de M′M={x-x′;-′;z-z′} y M″M={x″ x′;″-′;z″ a-z′} deben ser coplanares con el vector a=(a′,y″ y"), es decir, que (M′m, M″M, a)=0.
Por lo tanto, nuestra ecuación de un plano en el espacio se verá así:
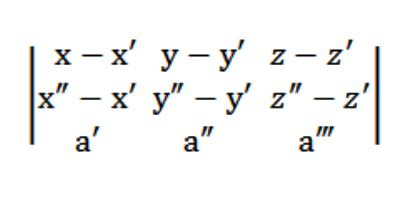
Tipo de la ecuación de un plano transversal a tres puntos de
Supongamos que tenemos tres puntos: (x′,el′,z′), (x″,el″,z″), (x', y",z"), que no pertenecen a la misma recta. Debe escribir la ecuación del plano que pasa a través de la especificados tres puntos. La teoría de la geometría afirma que este tipo de plano es realmente existe, eso es sólo ella es única e irrepetible. Dado que se trata de un plano cruza el punto (x′,el′,z′), la mirada de su ecuación será de la siguiente manera:
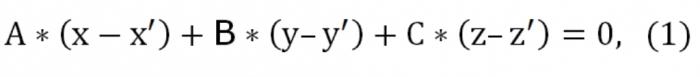
Aquí A, b, c diferente de cero al mismo tiempo. También definida en el plano de la cruza de dos puntos: (x″,el″,z″) y (x",y",z"). En este sentido, se deben realizar este tipo de condiciones:
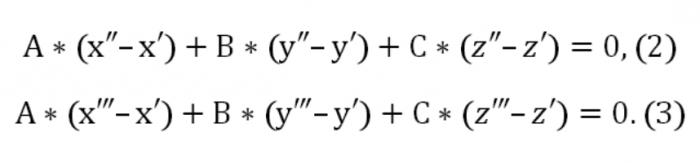
Ahora podemos crear un sistema homogéneo de ecuaciones (lineales) con los desconocidos u, v, w:
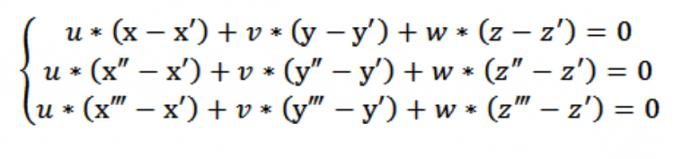
En nuestro caso, x,y o z actúa arbitraria de un punto que satisface la ecuación (1). Teniendo en cuenta la ecuación (1) y el sistema de ecuaciones (2) y (3), el sistema de ecuaciones de la indicada en la figura anterior, cumple con el vector N (A,b,c), que es no trivial. Precisamente porque el determinante de este sistema es cero.
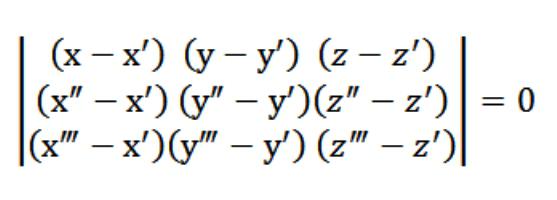
La Ecuación (1), que tenemos el resultado es la ecuación de un plano. A través de los 3 puntos se exactamente que pasa, y es fácil de comprobar. Para ello, hay que poner de nuestra determinante por los elementos que se encuentran en la primera línea. De las propiedades existentes identificador se desprende que nuestro plano al mismo tiempo cruza tres inicialmente los puntos (x′,el′,z′), (x″,el″,z″), (x', y",z"). Es decir, hemos decidido puesta ante nosotros la tarea.
Двухгранный el ángulo entre los planos
Двухгранный ángulo representa espacial geométrica de una figura formada por dos полуплоскостями, que se originan a partir de una recta. En otras palabras, es una parte del espacio, que se limita a los datos полуплоскостями.
Supongamos que disponemos de dos planos con las siguientes ecuaciones:
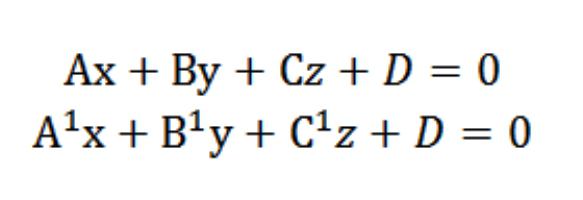
Sabemos que los vectores N=(A,b,c) y N¹=(A¹,En¹,Con¹) perpendiculares, de acuerdo con los planos. En este sentido, el ángulo φ entre los vectores N y N¹ equivale a la derecha (двухгранному), que se encuentra entre estos planos. Escalar la obra tiene la forma:
NN¹=|N||N¹|cos φ,
Precisamente porque
Cosφ= NN¹/|N||N¹|=(АА¹+ВВ¹+СС¹)/((√(А²+В²+С²))*(√(А¹)²+(В¹)²+(С¹)²)).
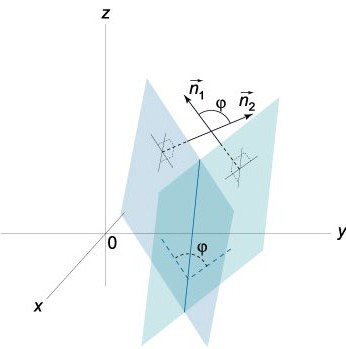
Basta con tener en cuenta que 0≤φ≤π.
En realidad dos planos que se cortan, forman dos ángulos (двухгранных): φ1 y φ2. La suma de sus es π (φ1+ φ2= π). En cuanto a sus cosenos, los valores absolutos no son iguales, pero son comerciales, es decir, cos φ1=-cos φ2. Si en la ecuación (0) sustituir A, b y c en los números -A, -b y -c respectivamente, entonces la ecuación que obtenemos, será la que determine este mismo plano, el único, el ángulo φ en la ecuación cos φ= NN1/|N||N1| a será sustituido por el π-φ.
La Ecuación de la perpendicular al plano de
Perpendiculares se llaman planos, entre los cuales el ángulo es de 90 grados. Usando el material expuesto anteriormente, podemos encontrar la ecuación de un planoperpendicular a la otra. Supongamos que tenemos dos planos: ah+vu+Cz+D=0 y Y¹x+A¹+¹z+D=0. Podemos afirmar que la perpendicular que va a ser, si cosφ=0. Esto significa que NN¹ a=aa¹+BB¹+ss¹=0.
La Ecuación de un plano paralelo
Paralelos se denominan dos planos, que no contienen los puntos comunes.
La Condición de paralelismo de los planos (sus ecuaciones son las mismas que en el párrafo anterior) es que los vectores N y N¹ que son perpendiculares, коллинеарные. Y esto significa que se cumplen las condiciones siguientes de la proporcionalidad:
A/A¹=/¹=s/s¹.
Si las condiciones de proporcionalidad son elevados - a/A¹=/¹=s/s¹=DD¹,
Esto indica que los datos del plano coinciden. Y esto significa que la ecuación de ah+vu+Cz+D=0 y Y¹x+A¹+¹z+D¹=0 describen un solo plano.
Distancia hasta el plano desde el punto de
Supongamos que tenemos un plano P, que se especifica en la ecuación (0). Es necesario encontrar la distancia de un punto con coordenadas (хₒ,уₒ,zₒ)=Qₒ. Para hacer esto, hay que citar la ecuación del plano P en la vista normal:
(ρ y,v)=p (p≥0).
En este caso ρ (x,y,z) es el radio-vector nuestro punto Q, situada en P, r – es la longitud de la perpendicular P, que fue lanzado desde el punto cero, v – es el único vector que se encuentra en la dirección de a.
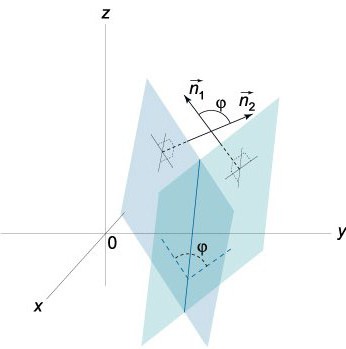
La Diferencia ρ-ρº el radio-vector de algún punto Q=(x,y,z), perteneciente Párrafo, así como el radio-vector de un punto especificado Q0=(хₒ,уₒ,zₒ) es el vector que el valor absoluto de la proyección que v es igual a la distancia d que es necesario encontrar desde Q0=(хₒ,уₒ,zₒ) hasta N:
D=|(ρ-ρ0,v)| pero
(ρ-ρ0,v)= (ρ y,v)–(ρ0,v) =r–(ρ0,v).
Así
D=|(ρ0,v)-p|.
Ahora puede ver que para calcular la distancia d de Q0 a un plano P, es necesario utilizar el tipo normal de la ecuación de un plano, transferir en la parte izquierda de la p, y en el último lugar de x,y,z sustituir (хₒ,уₒ,zₒ).
Por lo tanto, nos encontraremos con el valor absoluto obtenido de la expresión, es decir, la búsqueda de d.
El uso del idioma de los parámetros, obtenemos lo obvio:
D=|Ахₒ+Вуₒ+Czₒ|/√(A²+²+²).
Si el punto Q0 se encuentra al otro lado del plano P, como origen de coordenadas, entre el vector ρ-ρ0 y v se encuentra obtuso ángulo, por lo tanto:
D=-(ρ-ρ0,v)=(ρ0,v)-p>0.
En el caso de que el punto Q0, junto con el comienzo de las coordenadas se encuentra en la misma dirección de P, entonces se crea un ángulo agudo, es decir:
D=(ρ-ρ0,v)=r - (ρ0, v)>0.
Al final resulta, que en el primer caso (ρ0,v)>p, en el segundo (ρ0,v)<p.
El plano Tangente y la ecuación
Sobre el plano de la superficie en el punto táctil de Mº ¡ es un plano que contiene todas las tangentes a las curvas, realizadas a través de este punto en la superficie.
Con esta forma de la ecuación de la superficie F(x,y,z)=0 la ecuación del plano tangente tangente en el punto Mº xº,elº,zº) sería el siguiente:
FX(xº,elº,zº)(x - xº)+ FX(xº, elº, zº)(y - elº)+ FX(xº, elº,zº)(z-zº)=0.
Si se establece la superficie explícita z=f (x,y), entonces el plano tangente se describe por la ecuación:
Z-zº =f(xº, elº)(x - xº)+f(xº, elº)(y - elº).
La Intersección de dos planos
En el espacio tridimensional se encuentra el sistema de coordenadas (rectangular) Oxyz, dados dos planos P′ P″ que se cruzan y no coinciden. Porque cualquier tipo de plano, se encuentra en un sistema de coordenadas rectangular, se define como en la ecuación, vamos a suponer que P′ P″ se establecen las ecuaciones de A′x+A′+′z+D′ a=0 y Y″x+A″+″z+D″ a=0. En este caso tenemos la normal n′ (A′,En′,Con′) plano P′ y la normal n″ (A″,En″,Con″) plano P″. Debido a que nuestros planos no son paralelos y no coinciden, entonces estos vectores son no colineales. Usando el lenguaje de las matemáticas, nos esta condición podemos escribir como: n′≠ n″ ↔ (A′,En′,Con′) ≠ (λ*A″,λ*En″,λ*″), λϵR. Suelta directa, que se encuentra en la intersección de P′ P″ que, va a estar marcados con la letra a, en este caso, a = N′ ∩ P″.
¡ es la línea recta compuesta de una multiplicidad de todos los puntos (generales) de los planos P′ P″. Esto significa que las coordenadas de cualquier punto perteneciente a la recta y, al mismo tiempo debe satisfacer la ecuación de A′x+A′+′z+D′ a=0 y Y″x+A″+″z+D″ a=0. Entonces, las coordenadas del punto serán privados de la solución del siguiente sistema de ecuaciones:
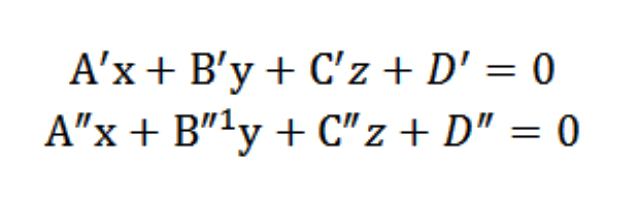
Al final resulta que la solución general de este sistema de ecuaciones será determinar las coordenadas de cada uno de los puntos de la recta, que será el punto de intersección P′ P″ y determinar la recta y en el sistema de coordenadas Oxyz (rectangular) en el espacio.
Article in other languages:

Alin Trodden - autor del artículo, editor
"Hola, soy Alin Trodden. Escribo textos, leo libros y busco impresiones. Y no soy mala para decírtelo. Siempre estoy feliz de participar en proyectos interesantes."
Noticias Relacionadas Con La
Catalina 2: biografía de la emperatriz. La Historia De Rusia
Ambigua personalidad fue catalina 2 la Gran – la emperatriz rusa de origen alemán. En la mayoría de los artículos y películas se muestra como un amante de los cortesanos bailes y lujosos baños, así como una gran cantidad de ...
El imperio español: la descripción, la historia y la bandera
el imperio Español en la época de su poder fue uno de los más grandes de los estados, que alguna vez haya existido en el mundo. Su creación sin interrupción se debe a la época de los Grandes descubrimientos geográficos, cuando se ...
Los grupos temáticos de las palabras, por ejemplo:
Que es la unidad de la lengua rusa? Sin duda, la palabra. Con su ayuda, nos comunicamos, compartimos mutuamente los pensamientos y experiencias. En este artículo se describen los grupos temáticos de las palabras que permiten clasi...
El país más poblado del mundo. Mónaco: datos interesantes sobre el principado
la Humanidad es muy desigualmente distribuido en la superficie de nuestro planeta. Por ejemplo, en la pequeña asiático estado puede alojar a más personas, que en general, el continente de australia. ¿Dónde está el país más poblado...
¿Qué es ледостав: definición y sus principales características
el Río – no es simplemente un curso de agua, несущийся de las montañas y elevaciones de los mares y océanos. Es bastante complicado ecosistema, una especie de cuerpo», que tiene sus propias características y modo...
De san petersburgo, el instituto del cine y la televisión da la bienvenida a los participantes
En rusia, hay universidades, la gloria que se extiende por europa. Entre ellos – el de san petersburgo, el instituto del cine y la televisión. Casi las tradiciones seculares de la institución garantizan la preparación de per...






















Comentarios (0)
Este artículo no tiene comentarios, se el primero!