Now - 16:27:24
Теңдеуі жазықтықта қалай жасауға болады? Түрлері теңдеулер жазықтықта
кеңістік жазықтық болады сұрақтар қоюға және әр түрлі тәсілдермен (бір нүктесі және векторы, екі нүкте және векторы, үш нүкте және т. б.). Дәл осыны ескере отырып, теңдеу жазықтықта болуы мүмкін түрлі түрлері. Сондай-ақ, белгілі шарттарды сақтай жазықтықта мүмкін параллель, перпендикулярными, пересекающимися және т. б. Туралы айтатын боламыз осы. Біз научимся құрайтын жалпы теңдеуі жазықтықта ғана емес.
Қалыпты түрі теңдеуі
Мысалы, бар кеңістік R3, ол тікбұрышты координаттық жүйесі XYZ. Зададим векторы α, ол шығарылды бастауыш нүктесінен О. Арқылы ұшы векторының α өткіземіз жазықтығы П, оған перпендикулярна.
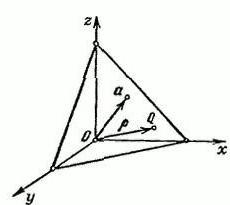
Белгілейміз Р. тараптың өз бетінше нүктесін Q=(х,у,z). Радиус-вектор нүктесі Q отырамыз әрпімен р. бұл вектордың ұзындығы α тең р=IαI және Ʋ=(cosα,cosβ,cosγ).
Бұл бірлік векторы бағытталған жаққа қарай, вектор α. α, β және γ « бұл бұрыштары құралатын арасындағы векторы Ʋ және оң бағыттары осі кеңістік х, у, z, тиісінше. Проекция қандай да бір нүктесінен QϵП " вектор Ʋ болып табылады тұрақты шама тең, р: (р,Ʋ) = р(р≥0).
Аталған теңдеуі мағынасы кезде р=0. Жалғыз жазықтық П жағдайда өтуге нүктесі Туралы (&альфа;=0), ол басталуы болып табылады координаттары, және бірлік вектор Ʋ шығарылған нүктесінен Туралы, перпендикулярен к П қарамастан, оның бағыты, яғни вектор Ʋ дейін дәлдікпен айқындалады белгісі. Алдыңғы теңдеуі болып табылады уравнением біздің жазықтықта П, айқын векторлық түрі. Ал координаттары оның түрі болады:
Көп:
Динамикалық және статикалық жұмыс бұлшық: айырмашылығы неде?
Динамикалық және статикалық жұмыс бұлшық үшін қажетті қалыпты жұмыс істеуі адам ағзасының орындау қозғалыстардың тән біздің телу. Адам ағзасы табиғатпен жасап шығарылды болатындай өте жақсы жеңе екеуімен де түрлері жүктеме. Динамикалық және статикалы...
Медицина колледжі медицина институтының қаласында Белгород жыл сайын қабылдайды, өзінің қанатының астына жүздеген студент облыс және жақын өңірлердің және жыл сайын шығарады мамандар орта медициналық білімі бар.қандай мамандықтар дайындайды мекемесі,...
Нервтік импульс, оның түрлендіру және беру тетігі
Жүйке жүйесі адам ретінде өзіндік үйлестірушісі біздің ағзамызда. Ол деп хабарлайды команданың ми мускулатуре, органдарға, тіндерге және өңдейді сигналдар шыққан олардан. Ретінде өзіндік тасығыштың деректер пайдаланылады жүйке серпін. Ол нені білдіре...
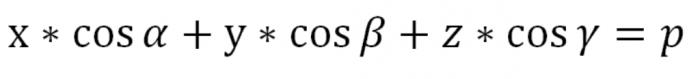
Р, мұнда көп немесе 0-ге тең. Біз тауып, кеңістіктегі жазықтық, түзу қалыпты.
Жалпы теңдеуі
Егер теңдеу " координаттардағы умножим кез келген саны, ол нөлге тең, теңдеу аламыз, балама осы айқындайтын ту ең жазықтық. Ол болуы тиіс мұндай түрі:
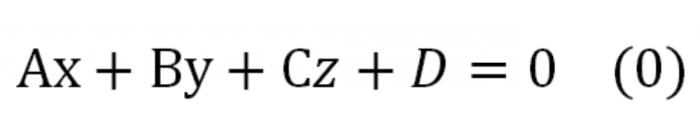
Мұнда А, В, С « бұл санының, бір мезгілде тамаша нөлден. Бұл теңдеу деп аталады теңдеу жазықтықтың жалпы түрі.
жазықтықтың Теңдеуі. Жеке жағдайға
Теңдеуі жалпы түрде болуы мүмкін видоизменяться болған қосымша жағдайлар. Қарастырайық олардың кейбіреулері.
Мысалы, А коэффициенті 0-ге тең. Бұл білдіреді, бұл жазықтық параллельна берілген осі Ох. Бұл жағдайда теңдеуінің түрі өзгереді: Ву+Cz+D=0.
осыған Ұқсас түрі теңдеуі, өзгеріп отырады және мынадай жағдайларда:
- біріншіден, егер=0, онда теңдеу өзгереді Ах+Cz+D=0, куәландырады туралы параллельности осі Оу.
- Екіншіден, егер С=0 болса, онда теңдеу-ға өзгертіледі Ах+Ву+D=0, бұл туралы айтуға параллельности - берілген осі Oz.
- үшіншіден, егер D=0, теңдеуі болады сияқты көрінеді Ах+Ву+Cz=0, ол білдіреді жазықтығы қиып өтеді (координаттар басы).
- төртіншіден, егер A=B=0 болса, онда теңдеу өзгереді Cz+D=0 болады деп дәлелдеуге параллельность - Oxy.
- бесіншіден, егер B=C=0 болса, онда теңдеу болады Ах+D=0, ал бұл жазықтық - Oyz параллельна.
- алтыншыдан, егер A=C=0 болса, онда теңдеу біреуі түрі Ву+D=0 болса, онда бар болады туралы хабарлауға параллельности - Oxz.
Түрі теңдеулер бөліктердегі
Бұл жағдайда санының А, В, С, D отличны от нөлге түрі теңдеу (0) болуы мүмкін мынадай:
х/а + у/b + z/ = 1,
а = -D/А, b = -D/, = - D/С болады.
Аламыз нәтижесінде теңдеуі жазықтықта бөліктердегі. Айта кету керек, бұл жазықтық болады өтуге Ох осі нүктесінде координаттары бар (а,0,0), Ок « (0,в,0), ал Oz « (0,0,с).
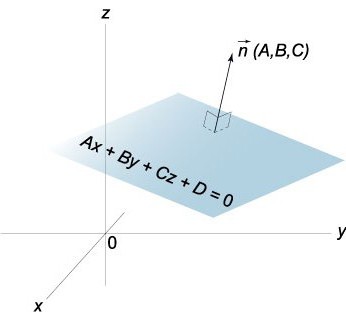
ескере Отырып, теңдеу х/а + у/b + z/ = 1 қиын емес көзбен ұсынуға орналастыру жазықтықта қатысты берілген координаталық жүйелер.
Координаттары қалыпты вектордың
Қалыпты векторы n жазықтығына П бар координаттары болып табылатын коэффициенттерімен жалпы теңдеуі осы жазықтықта, яғни n (А,В,С).
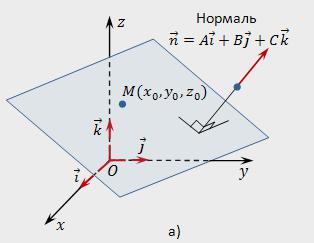
анықтау Үшін координаттары норманың n, білу жеткілікті жалпы теңдеуі берілген жазықтықта.
пайдаланған Кезде теңдеулер бөліктердегі, ол түрі х/а + у/b + z/ = 1, және пайдалану кезінде жалпы теңдеуі болады координаттарын кез келген қалыпты вектордың берілген жазықтық: (1/а + 1/в + 1/с).
Айта кету керек, қалыпты векторы шешуге көмектеседі әр түрлі міндеттері. Ең көп таралған жатады міндеттері саятын дәлелдеу перпендикулярности немесе параллельности жазықтықтың, міндеттері бойынша іздеу бұрыштарының арасындағы жазықтықтармен немесе бұрыштарының арасындағы жазықтықтың және түзу.
Түрі теңдеуі жазықтықта сәйкес координаттар нүктелері және қалыпты вектордың
Ненулевой векторы n, перпендикулярный берілген жазықтық деп атайды қалыпты (нормалью) берілген жазықтықта.
Мысалы, координатном кеңістікте тік бұрышты координаталық жүйесі) Oxyz қойған:
- нүкте Мₒ координаттары бар (хₒ,уₒ,zₒ);
- нөлдік векторы n=А*i+*j+С*k.
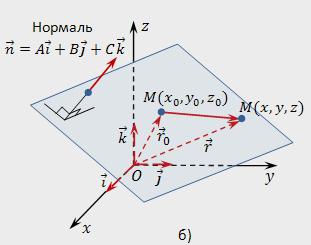
жасау Керек теңдеуі жазықтықта өтеді нүктесі арқылы Мₒ перпендикуляр норманың n.
кеңістікте таңдаймыз кез келген тараптың еркін нүктесін белгілейміз және оны М (х, у,z). Пускайрадиус-векторы кез келген нүкте М (х,у,z), r=х*i+y*j+z*k, ал радиус-вектор нүктесі Мₒ (хₒ,уₒ,zₒ) « rₒ=хₒ*i+уₒ*j+zₒ*k. Нүктесі М тиесілі болады берілген жазықтықта, егер вектор МₒМ болады перпендикулярен вектору n. Запишем шарт ортогональности көмегімен тақырып:
[МₒМ, n] = 0.
Өйткені МₒМ = r«rₒ, векторлық теңдеуі жазықтықта дұрыс сияқты көрінеді де:
[r « rₒ, n] = 0.
Бұл теңдеу болуы мүмкін және басқа да нысаны. Бұл үшін пайдаланылады қасиеттері тақырып, ал қайта құрылып жатыр сол жағы теңдеулер. [r « rₒ, n] = [r, n] – [rₒ, n]. Егер [rₒ, n] ретінде белгілеуге, онда, сонда мынадай теңдеу: [(r) n] – с = 0 немесе [r, n] = с, ол білдіреді тұрақтылығы проекциялар қалыпты векторы радиус-векторлар берілген нүктелер тиесілі жазықтықта.
алуға болады координаталық түрі жазу векторлық теңдеулері біздің жазықтықта [r « rₒ, n] = 0. Себебі r«rₒ = (х«хₒ)*i + («уₒ)*j + (z«zₒ)*k, n = А*i+*j+С*k, біз:
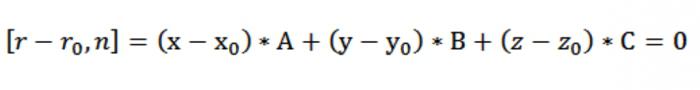
Шығады, бізде құрылады теңдеуі жазықтықта арқылы өтетін нүктесін перпендикуляр норманың n:
А*(х - хₒ)+*(« уₒ)*(z«zₒ)=0.
Түрі теңдеуі жазықтықта сәйкес координаттар екі нүкте мен вектордың коллинеарного жазықтықта
Зададим екі еркін нүкте М′ (х′,′,z′) мен М″ (х″,″,z″), сондай-ақ векторы, ал (а′,а″ а").
Енді біз аламыз жасау теңдеуі берілген жазықтықта, ол арқылы өтеді қолда бар нүктелері М′ М″, сондай-ақ әртүрлі нүктесін М координаттары (х,у,z) параллель берілген вектору а.
бұл векторлар М′М={х-х′;у-у′;z-z′} М″М={х″-х′;у″-′;z″-z′} тиіс компланарными с векторы а=(а′,а″ а"), ал бұл дегеніміз, бұл (М′М, М″М, а)=0.
Сонымен, біздің кеңістіктегі жазықтық, түзу сияқты көрінеді:
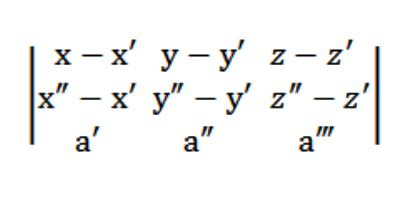
Түрі теңдеуі жазықтықта, пересекающей үш нүктеге
Мысалы, бізде үш нүкте: (х′,′,z′), (х″,″,z″), ("х,у"," z) тиесілі емес бір тік. Жазу қажет теңдеуі жазықтықта арқылы өтетін берілген үш нүкте. Теориясы геометрия бекітеді, бұл мұндай жазықтығы шынымен бар, бірақ ол жалғыз және қайталанбас. Өйткені бұл жазықтық қиып өтетін нүктесін (х′,′,z′), оның түрі теңдеуі мынадай болады:
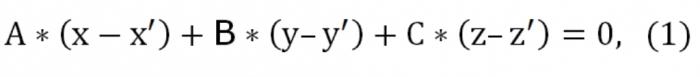
Мұнда А, В, С жақсы нөлден бір мезгілде. Сондай-ақ, берілген жазықтық қиып өтіп, тағы екі нүкте: (х″,″,z″) және ("х,у"," z). Осыған байланысты, орындалуы тиіс осындай шарттары:
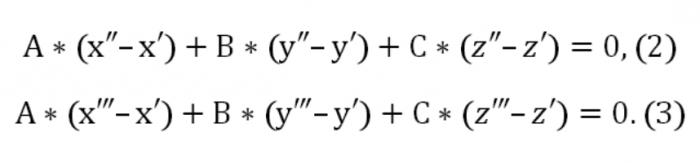
Қазір біз жасауға біртекті теңдеулер жүйесін (сызықтық) белгісіз u, v, w:
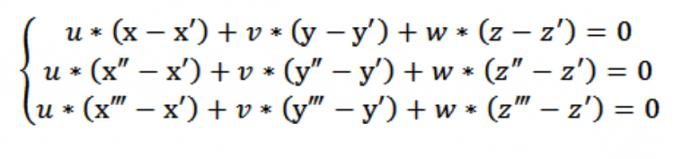
біздің жағдайда х,у немесе z сөйлейді, еркін нүктесі, ол қанағаттандырады теңдеу (1). Ескере отырып, теңдеу (1) және жүйесі-дан теңдеулер (2) және (3) теңдеулер жүйесі, көрсетілген суретте жоғарыда қанағаттандырады векторы N (А,В,С), ол болып табылады нетривиальным. Сондықтан анықтаушы осы жүйенің нөлге теңестіріледі.
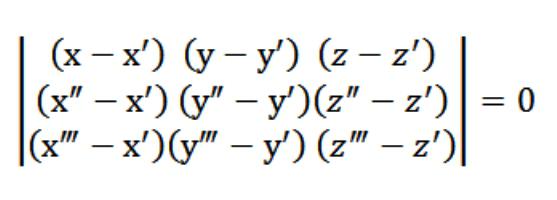
Теңдеу (1), бізде, бұл теңдеу жазықтықта. 3 нүктесінің ол дәл өтуде, және бұл оңай тексеруге болады. Ол үшін таратуға біздің анықтаушы элементтері бойынша орналасқан, бірінші жолда. Қолданыстағы қасиеттерін определителя туындамаса, біздің жазықтығы бір уақытта қиып өтеді үш бастапқыда берілген нүктесінен (х′,′,z′), (х″,″,z″), ("х,у"," z). Яғни, біз осы қойған алдымызға міндет қойды.
Двухгранный жазықтықтың арасындағы бұрыш
Двухгранный бұрышы білдіреді кеңістіктік геометриялық фигураны құрылған екі полуплоскостями құрып, бір түзу. Басқаша айтқанда, бұл кеңістік, ол шектеледі деректермен полуплоскостями.
Мысалы, бізде екі жазықтықта мынадай уравнениями:
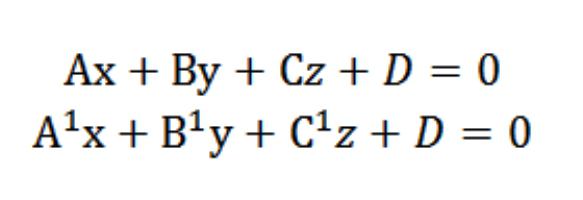
Бізге белгілі векторы N=(А,В,С) және N¹=(А¹,¹,¹) перпендикулярны сәйкес берілген жазықтықта. Осыған байланысты бұрыш φ аныс векторлар N және N¹ тең бұрышы (двухгранному), ол осы жазықтықтармен. Скаляр көбейтіндісі түрі бар:
NN¹=|N||N¹|cos φ
сондықтан
Cosφ= NN¹/|N||N¹|=(АА¹+ВВ¹+СС¹)/((√(А²+В²+С²))*(√(А¹)²+(В¹)²+(С¹)²)).
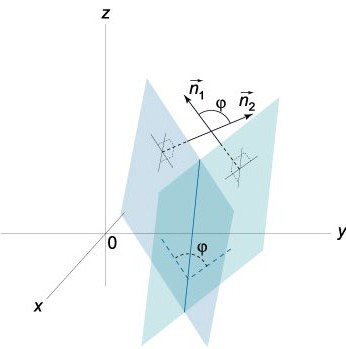
Жеткілікті ескерілсін 0≤φ≤π.
шын мәнінде, екі жазықтықта, олар түйісетін құрайды екі бұрышының (двухгранных): φ1 φ2. Сомасы олардың тең π (φ1+ φ2= π). Бұл олардың косинусов, онда олардың абсолюттік шамасына тең, бірақ ерекшеленеді олар белгілермен, яғни cos φ1=-cos φ2. Егер теңдеулер (0) деген сөздер мен сандар -А -, - және -тиісінше, онда теңдеу, біз анықтауға болады, сол жазықтық, жалғыз, бұрыш φ теңдеулер cos φ= N1/|N||N1| болады ауыстырылуы π-φ.
Теңдеуі перпендикуляр жазықтықта
Перпендикулярными деп аталады жазықтықта, араларында бұрышы 90 градусқа тең. Пайдалана отырып, материал баяндалған жоғарыда біз таба теңдеу жазықтықта,перпендикуляр басқа. Мысалы, бізде екі жазықтықта: Ах+Ву+Cz+D=0 және А¹х+¹у+С¹z+D=0. Біз айта аламыз перпендикулярными олар, егер cosφ=0. Бұл дегеніміз, NN¹=АА¹+ВВ¹+СС¹=0.
Теңдеуі параллель жазықтықта
Параллель деп аталады екі жазықтықта емес, оларда ортақ нүкте.
Шарт-параллельности жазықтығының (олардың теңдеулері бірдей және алдыңғы тармақта) ерекшелігі векторлары N және N¹, оларға перпендикулярны, коллинеарные. Бұл мынадай шарттар орындалады үйлесімділік:
А/А¹=/¹=С/С¹.
Егер үйлесімділік болып табылады кеңейтілген - А/А¹=/¹=С/С¹=DD¹
бұл туралы куәландырады деректер жазықтықта сәйкес келеді. Бұл теңдеу Ах+Ву+Cz+D=0 және А¹х+¹у+С¹z+D¹=0 сипаттайды бір жазықтығы.
Қашықтығы жазықтықта нүктеден
Мысалы, бізде жазықтығы П, бойда уравнением (0). Табу керек оған дейін қашықтық координаттары бар нүктелер (хₒ,уₒ,zₒ)=Qₒ. Оны істеу керек келтіру теңдеуі жазықтықта П қалыпты түрі:
(ρ v)=р (р≥0).
егер ρ (х,у,z) болып табылады радиус-векторы біздің нүктесінен Q орналасқан П, р « бұл ұзындығы перпендикуляр П, ол шығарылды бірі-нөлдік нүктеге v – бұл бірлік вектор, ол бағытында орналасқан а.
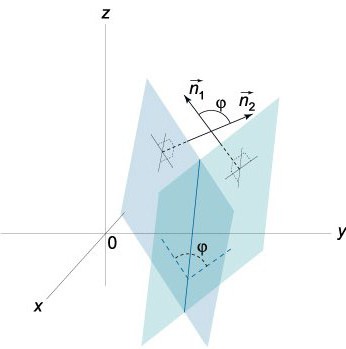
Айырмашылық ρ-ρº радиус-векторының қандай да бір нүктеге Q=(х,у,z), П тиесілі, сондай-ақ радиус-векторының берілген нүктеден Q0=(хₒ,уₒ,zₒ) болып табылады, мұндай векторы, абсолюттік шамасы проекцияда оның v тең қашықтық d, ол табу қажет желтоқсандағы Q0=(хₒ,уₒ,zₒ) П:
D=|(ρ-ρ0,v)|, бірақ
(ρ-ρ0,v)= (ρ v)«(ρ0,v) =р«(ρ0,v).
Міне,
D=|(ρ0,v)-а|.
Енді көрініп есептеу үшін қашықтық d Q0 дейінгі жазықтықта П, керек қалыпты түрі теңдеуі жазықтықта, бұл ретте ауыстыру сол жақ бөлігін р, ал соңғы орнына х,у,z подставить (хₒ,уₒ,zₒ).
осылайша, біз табамыз абсолюттік мәні алынған білдіру, яғни искомое d.
Пайдалана отырып, тіл параметрлерді аламыз айқын:
D=|Ахₒ+Вуₒ+Czₒ|/√ А²+²+²).
Егер берілген нүкте Q0 орналасқан екінші жағына жазықтықта П, координаталардың басталуы болса, онда векторы арасындағы ρ-ρ0 және v орналасқан доғал бұрышы, сондықтан да:
D=-(ρ-ρ0,v)=(ρ0,v)-р>0.
Бұл жағдайда нүктесі Q0 - мен бірлесіп басталуы координаттар бойынша орналастырылады бір жағына П, онда құратын бұрышы өткір, яғни:
D=(ρ-ρ0,v)=р - (ρ0, v)>0.
сөйтіп, бірінші жағдайда (ρ0,v)>р, екінші (ρ0,v)<р.
Касательная жазықтық және оның теңдеуі
Қатысты жазықтық бетіне жанасу нүктесінде Мº « бұл жазықтық қамтитын барлық мүмкін болатын жанама - қисықтары, арқылы жүргізілген бұл нүкте жер бетінде.
осындай түріндегі теңдеу бетінің F(х,у,z)=0 теңдеуі жанама жазықтықта жанама нүктесінде Мº(хº,º,zº) сияқты көрінеді:
Fх(xº,º,zº)(х - хº)+ Fх(xº,º, zº)(у - уº)+ Fх(xº,º,zº)(z-zº)=0.
Егер қою беті айқын нысанда z=f (х,у), онда касательная жазықтық баяндалады уравнением:
Z-zº =f(хº,º)(х - хº)+f(хº,º)(у - уº).
Қиылысы екі жазықтықтың
В трехмерном пространстве орналасқан координаттар жүйесі (тік бұрышты) Oxyz берілді, екі жазықтықтың П′ Р″ олар түйісетін және сәйкес келмейді. Өйткені кез келген жазықтық, находящаяся в тік бұрышты координаталық жүйе анықталады жалпы уравнением боламыз деп пайымдауға П′ Р″ қойылады уравнениями А′х+′у+С′z+D′=0 және А″х+″у+С″z+D″=0. Мұндай жағдайда бізде қалыпты n′ А′,′,′) жазықтықта П′ және қалыпты n″ А″,″,″) жазықтықта П″. Өйткені біздің жазықтықта емес, бір-біріне параллельді және сәйкес келмесе, онда бұл векторлар болып табылады коллинеарными. Пайдалана отырып, тілі, математика, біз, осы шарт жазып аламыз: n′≠ n″ ↔ А′,′,′) ≠ (λ*А″,λ*″,λ*″), λϵR. Пускай тікелей, ол жатыр қиылысында П′ Р″, белгіленуі әрпімен а, бұл жағдайда а = П′ ∩ П″.
ал « бұл тікелей көптеген бейнелерден тұратын барлық нүктелер (жалпы) жазықтықтың П′ Р″. Бұл координаттары кез келген нүктесіне тиесілі тікелей а тиіс бір мезгілде қанағаттандыруға теңдеулер А′х+′у+С′z+D′=0 және А″х+″у+С″z+D″=0. Демек, нүкте координаталары болады жеке шешімімен келесі теңдеулер жүйесінің:
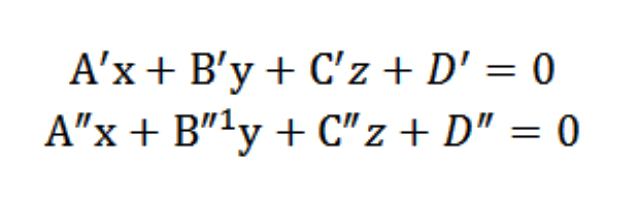
сөйтіп, шешім (жалпы) осы теңдеулер жүйесінің анықтауға болады координаттары әрбір нүктесі тікелей, ол болуға қиылысу нүктесі П′ Р″, анықтау және тікелей ал координаталық жүйесі Oxyz (тік бұрышты) кеңістікте.
Article in other languages:

Alin Trodden - мақала авторы, редактор
"Сәлем, Мен Алин Тродденмін. Мен мәтіндер жазып, кітаптар оқып, әсер іздеймін. Мен сізге бұл туралы айтуды жақсы білемін. Мен әрқашан қызықты жобаларға қатысқаныма қуаныштымын."
Жаңалықтар
Екатерина 2: өмірбаяны императрицы. Ресей Тарихы
Неоднозначной тұлға болды Екатерина 2 Ұлы « ресей императрица тегі неміс. Көптеген мақалалар мен фильмдерді ол көрсетілді ретінде любительница сарай маңындағы балл және сәнді дәретхана, сондай-ақ көптеген үміткерлердің отыры...
Испан империясы: сипаттамасы, тарихы мен туы
Испан империясы заманында, өз күш-қуатын болды ірі мемлекеттердің-соңды әлемде. Оны құру неотрывно байланысты дәуірі Ұлы географиялық ашулар, ол болды отарлық держава. Бірнеше ғасырлар бойы ту Испан империясының дамыды үстінен үлк...
бірлігі Не болып табылады орыс тілі? Әрине, сөз. Оның көмегімен біз араласамыз, тышқанның бір-біріне ойлар мен уайымдар. Мақалада тақырыптық сөздерді, жіктеуге мүмкіндік беретін байлық орыс тілі, насчитывающего өзінің әдеби сөздіг...
Ең густонаселенная елі әлемдегі. Монако: қызықты фактілер туралы князьдігіндегі
Адамзат біркелкі емес бөлінуі жөніндегі беті біздің планета. Мысалы, шағын азиялық мемлекетте тұруы мүмкін көп адамдарды қарағанда, тұтастай ұйымдастырылады Австралия. Онда да ең густонаселенная ел? Және ол қызықты? Талдап көрейік...
Осындай мұз қату: ұғымының анықтамасы және оның басты ерекшеліктері
Өзен – бұл жай ғана водоток, несущийся қалалық және жерден аласа жерге түсу керек теңіздер мен мұхиттар. Бұл өте күрделі экожүйе, өзіндік «адам ағзасына», оған тән ерекшеліктері мен режимдері. Осы туралы айтылады...
Нені зерттейді гидролог? Зерттеу пәні гидрология кафедрасы
Су – бұл ең маңызды табиғи ресурстар Жер бетінде, онда нені зерттейді гидролог. Онсыз өмір мүмкін емес еді. Дегенмен судың жаһандық мағынада өте көп, ол емес, әрқашан қажетті уақытта, қажетті жерде, қажетті уақытта және тала...





















Комментарий (0)
Бұл мақала емес, түсіндірмелер, бірінші болыңыз!