Now - 20:58:04
Раўнанне плоскасці: як скласці? Віды раўнанняў плоскасці
У прасторы плоскасць можна задаваць рознымі спосабамі (адной кропкай і вектарам, двума кропкамі і вектарам, трыма кропкамі і інш.). Менавіта з улікам гэтага раўнанне плоскасці можа мець розныя віды. Таксама пры выкананні пэўных умоў плоскасці могуць быць паралельнымі, перпендыкулярнымі, перасякальнымі і г. д. Пра гэта і пагаворым у дадзеным артыкуле. Мы навучымся складаць агульнае раўнанне плоскасці і не толькі.
Нармальны выгляд ўраўненні
Дапусцім, ёсць прастора R3, якое мае прастакутную каардынатную сістэму XYZ. Задамо вектар α, які будзе выпушчаны з пачатковай кропкі А. Праз канец вектару α правядзем плоскасць П, якая будзе перпендыкулярная яму.
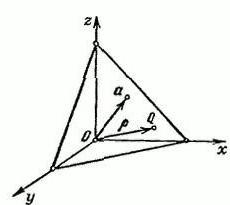
Пазначым на П адвольную кропку Q=(х,у,z). Радыус-вектар кропкі Q падпішам літарай н. Пры гэтым даўжыня вектара α складае р=IαI і Ʋ=(cosα,cosβ,cosγ).
Гэта адзінкавы вектар, накіраваны ў бок, як і вектар α. α, β і γ – гэта куты, якія ўтвараюцца паміж вектарам Ʋ і станоўчымі напрамкамі восяў прасторы х, у, z адпаведна. Праекцыя якой-небудзь пункту QϵП на вектар Ʋ з'яўляецца пастаяннай велічынёй, якая роўная р: (р,Ʋ) = р(р≥0).
Азначанае раўнанне мае сэнс, калі р=0. Адзінае, плоскасць П у гэтым выпадку будзе перасякаць кропку Аб (α=0), якая з'яўляецца пачаткам каардынат, і адзінкавы вектар Ʋ, выпушчаны з кропкі Аб, будзе перпендыкулярны да П, нягледзячы на яго кірунак, што азначае, што вектар Ʋ вызначаецца з дакладнасцю да знака. Папярэдняе раўнанне з'яўляецца раўнаннем нашай плоскасці П, выяўленым у вектарнай форме. А вось у каардынатах яго выгляд будзе такім:
Больш:
Нервовы імпульс, яго пераўтварэнне і механізм перадачы
Нервовая сістэма чалавека выступае своеасаблівым каардынатарам у нашым арганізме. Яна перадае каманды ад мозгу мускулатуры, органаў, тканін і апрацоўвае сігналы, якія ідуць ад іх. У якасці своеасаблівага носьбіта дадзеных выкарыстоўваецца нервовы імп...
Куды паступаць пасля 11 класа? Якую выбраць прафесію?
Пры выбары сваёй будучай прафесіі не варта абапірацца на чые-то рэкамендацыі і парады, тым больш не трэба падпарадкоўвацца сваім бацькам, якія даволі часта вырашаюць без вас самастойна, куды паступіць пасля 11 класа. Варта задумацца, наколькі паспяхо...
Крывяносная сістэма жывёл, як вынік эвалюцыйнага развіцця свету
Крывяносная сістэма жывёл прайшла доўгі шлях фарміравання ў ходзе эвалюцыйнага развіцця свету. Яна ўтварылася на месцы рудыментарных частак першаснай паражніны цела, якая ў вышэйшых жывёл была выцесненая целломом, або другаснай паражніной цела. У пра...
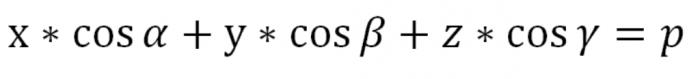
Р тут больш або роўна 0. Мы знайшлі раўнанне плоскасці ў прасторы ў нармальным выглядзе.
Агульная раўнанне
Калі раўнанне ў каардынатах памножым на любы лік, якое не роўна нулю, атрымаем раўнанне, эквівалентнае гэтым, вызначальнае тую самую плоскасць. Яно будзе мець такі выгляд:
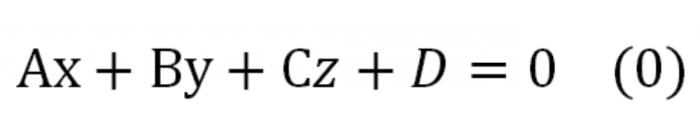
Тут А, У, З – гэта колькасці, адначасова выдатныя ад нуля. Гэта раўнанне называецца як раўнанне плоскасці агульнага выгляду.
Ўраўненні плоскасцяў. Прыватныя выпадкі
Раўнанне ў агульным выглядзе можа відазмяняцца пры наяўнасці дадатковых умоў. Разгледзім некаторыя з іх.
выкажам здагадку, што каэфіцыент А роўны 0. Гэта азначае, што дадзеная плоскасць раўналежная зададзенай восі Ох. У гэтым выпадку выгляд ўраўненні зменіцца: Ву+Cz+D=0.
Аналагічна выгляд ўраўненні будзе змяняцца і пры наступных умовах:
- Па-першае, калі У=0, то раўнанне зменіцца на Ах+Cz+D=0, што будзе сведчыць аб паралельнасці да восі Оу.
- Па-другое, калі З=0, то раўнанне пераўтворыцца ў Ах+Ву+D=0, што будзе казаць аб паралельнасці да зададзенай восі Oz.
- па-трэцяе, калі D=0, раўнанне будзе выглядаць як Ах+Ву+Cz=0, што будзе азначаць, што плоскасць перасякае О (пачатак каардынат).
- У-чацвёртае, калі A=B=0, то раўнанне зменіцца на Cz+D=0, што будзе даказваць раўналежнасць да Oxy.
- па-пятае, калі B=C=0, то раўнанне стане Ах+D=0, а гэта азначае, што плоскасць да Oyz раўналежная.
- па-шостае, калі A=C=0, то раўнанне набудзе выгляд Ву+D=0, то значыць будзе паведамляць аб паралельнасці да Oxz.
Выгляд ўраўненні ў адрэзках
У выпадку, калі лікі А, У, З, D выдатныя ад нуля, выгляд ўраўненні (0) можа быць наступным:
х/а + у/b + z/з = 1,
у якім а = -D/А, b = -D/У, з = -D/С.
Атрымліваем у выніку раўнанне плоскасці ў адрэзках. Варта адзначыць, што дадзеная плоскасць будзе перасякаць вось Ох у пункце з каардынатамі (а,0,0), Оу – (0,b,0), а Oz – (0,0,з).
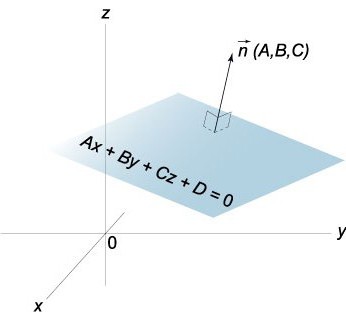
З улікам раўнання х/а + у/b + z/з = 1 няцяжка візуальна прадставіць размяшчэнне плоскасці адносна зададзенай каардынатнай сістэмы.
Каардынаты нармальнага вектара
Нармальны вектар n да плоскасці П мае каардынаты, якія з'яўляюцца каэфіцыентамі агульнага ўраўненні дадзенай плоскасці, то ёсць n (А,У,З).
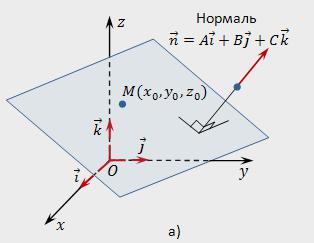
Для таго каб вызначыць каардынаты нармалі n, дастаткова ведаць агульнае раўнанне зададзенай плоскасці.
Пры выкарыстанні ўраўненні ў адрэзках, якое мае выгляд х/а + у/b + z/з = 1, як і пры выкарыстанні агульнага ўраўненні, можна запісаць каардынаты любога нармальнага вектара зададзенай плоскасці: (1/ + 1/b + 1/з).
Варта адзначыць, што нармальны вектар дапамагае вырашыць разнастайныя задачы. Да самым распаўсюджаным ставяцца задачы, якія складаюцца ў доказе перпендыкулярнасці або паралельнасці плоскасцяў, задачы па знаходжанню вуглоў паміж плоскасцямі або кутоў паміж плоскасцямі і прамымі.
Выгляд ўраўненні плоскасці згодна каардынатам кропкі і нармальнага вектара
Ненулявое вектар n, перпендыкулярны зададзенай плоскасці, называюць нармальным (нармаллю) для зададзенай плоскасці.
выкажам здагадку, што ў координатном прасторы (прастакутнай каардынатнай сістэме) Oxyz зададзены:
- кропка Мₒ з каардынатамі (хₒ,уₒ,zₒ);
- нулявы вектар n=А*i+У*j*k.
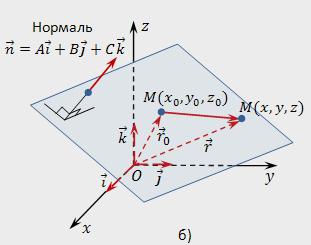
Трэба скласці раўнанне плоскасці, якая будзе праходзіць праз кропку Мₒ перпендыкулярна нармалі n.
У прасторы абярэм любую адвольную кропку і пазначым яе М (х, у,z). Няхайрадыус-вектар кожнай кропкі М (х,у,z) будзе r=х*i+y*j+z*k, а радыус-вектар кропкі Мₒ (хₒ,уₒ,zₒ) – rₒ=хₒ*i+уₒ*j+zₒ*k. Кропка М будзе належаць зададзенай плоскасці, калі вектар МₒМ будзе перпендыкулярны вектару n. Запішам умову артаганальнай пры дапамозе скалярнага творы:
[МₒМ, n] = 0.
Паколькі МₒМ = r–rₒ, вектарнае раўнанне плоскасці будзе выглядаць так:
[r – rₒ, n] = 0.
Дадзенае раўнанне можа мець і іншую форму. Для гэтага выкарыстоўваюцца ўласцівасці скалярнага творы, а пераўтвараецца левы бок ўраўненні. [r – rₒ, n] = [r, n] – [rₒ, n]. Калі [rₒ, n] пазначыць як з, то атрымаецца наступнае раўнанне: [r, n] – з = 0 або [r, n] = з, якое выказвае сталасць праекцый на нармальны вектар радыус-вектараў зададзеных кропак, якія належаць плоскасці.
Цяпер можна атрымаць координатный выгляд запісу вектарнага ўраўненні нашай плоскасці [r – rₒ, n] = 0. Паколькі r–rₒ = (х–хₒ)*i + (у–уₒ)*j + (z–zₒ)*k, а n = А*i+У*j*k, мы маем:
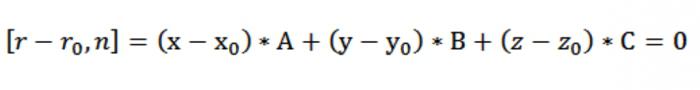
Выходзіць, у нас ўтвараецца раўнанне плоскасці, якая праходзіць праз кропку перпендыкулярна нармалі n:
А*(х - хₒ)+У*(у– уₒ)З*(z–zₒ)=0.
Выгляд ўраўненні плоскасці згодна каардынатах дзвюх кропак і вектара, коллинеарного плоскасці
Задамо дзве адвольныя пункту М′ (х′,у′,z′) і М″ (х″,у″,z″), а таксама вектар а (а′,а″,а").
Цяпер мы зможам скласці раўнанне зададзенай плоскасці, якая будзе праходзіць праз наяўныя пункту М′ і М″, а таксама ўсякую кропку М з каардынатамі (х,у,z) паралельна зададзеным вектары а.
Пры гэтым вектары М′М={х-х′;у-у′;z-z′} і M″М={х″-х′;ў″-у′;z″-z′} павінны быць компланарными з вектарам а=(а′,а″,а"), а гэта значыць, што (М′М, М″М, а)=0.
такім чынам, наша раўнанне плоскасці ў прасторы будзе выглядаць так:
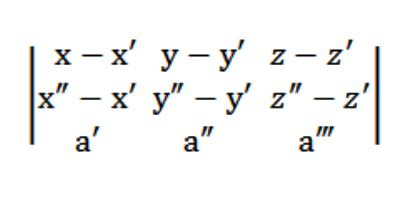
Выгляд ўраўненні плоскасці, якая перасякае тры кропкі
Дапушчальны, у нас ёсць тры кропкі: (х′,у′,z′), (х″,у″,z″), (х",у",z"), якія не належаць адной прамой. Неабходна напісаць раўнанне плоскасці, якая праходзіць праз тры зададзеныя кропкі. Тэорыя геаметрыі сцвярджае, што такога роду плоскасць сапраўды існуе, вось толькі яна адзіная і непаўторная. Паколькі гэтая плоскасць перасякае кропку (х′,у′,z′), выгляд яе ўраўненні будзе наступным:
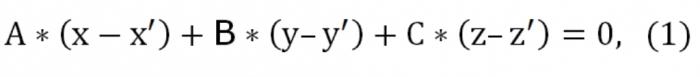
Тут А, У, З выдатныя ад нуля адначасова. Таксама зададзеная плоскасць перасякае яшчэ дзве кропкі: (х″,у″,z″) і (х",у",z"). У сувязі з гэтым павінны выконвацца такога роду ўмовы:
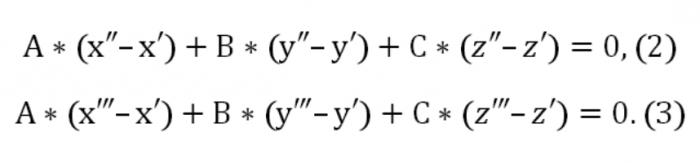
Цяпер мы можам скласці аднастайную сістэму раўнанняў (лінейную) з невядомымі u, v, w:
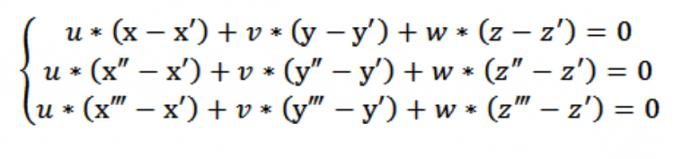
У нашым выпадку х,у, z выступае адвольнай кропкай, якая задавальняе раўнанне (1). Улічваючы раўнанне (1) і сістэму з раўнанняў (2) і (3), сістэмы раўнанняў, паказанай на малюнку вышэй, задавальняе вектар N (А,У,З), які з'яўляецца нетрывіяльным. Менавіта таму вызначальнік дадзенай сістэмы складае нуля.
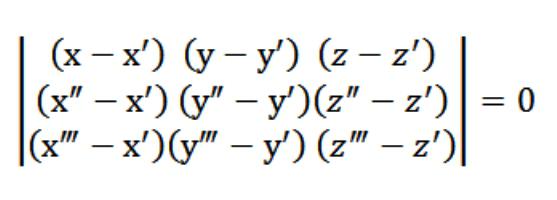
Раўнанне (1), якое ў нас атрымалася, гэта і ёсць раўнанне плоскасці. Праз 3 пункту яна сапраўды праходзіць, і гэта лёгка праверыць. Для гэтага трэба раскласці наш вызначальнік па элементах, якія знаходзяцца ў першай радку. З існуючых уласцівасцяў вызначальніка вынікае, што наша плоскасць адначасова перасякае тры першапачаткова зададзеныя кропкі (х′,у′,z′), (х″,у″,z″), (х",у",z"). Гэта значыць, мы вырашылі пастаўленую перад намі задачу.
Двухгранный кут паміж плоскасцямі
Двухгранный кут ўяўляе сабой прасторавую геаметрычную фігуру, адукаваную двума полуплоскостями, якія зыходзяць з адной прамой. Іншымі словамі, гэта частка прасторы, якая абмяжоўваецца дадзенымі полуплоскостями.
Дапусцім, у нас маюцца дзве плоскасці з наступнымі раўнаннямі:
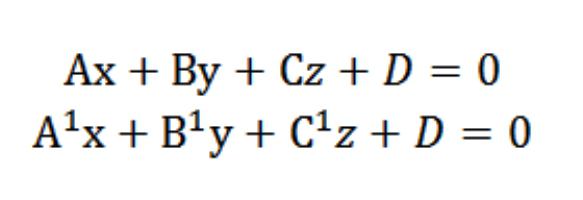
Нам вядома, што вектары N=(А,У,З) і N¹=(А¹,У¹,¹) перпендыкулярныя згодна з зададзеным плоскасцях. У сувязі з гэтым кут φ між вектарамі N і N¹ складае куце (двухгранному), які знаходзіцца паміж гэтымі плоскасцямі. Скалярны твор мае выгляд:
NN¹=|N||N¹|cos φ,
менавіта таму,
Cosφ= NN¹/|N||N¹|=(АА¹+ВВ¹+СС¹)/((√(А²+В²+С²))*(√(А¹)²+(В¹)²+(С¹)²)).
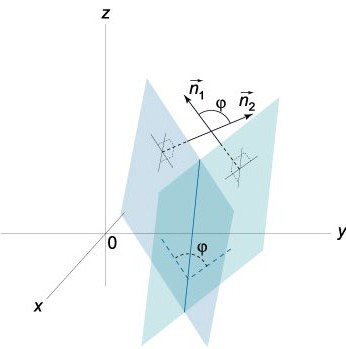
Дастаткова ўлічыць, што 0≤φ≤π.
На самай справе дзве плоскасці, якія перасякаюцца, ўтвараюць два кута (двухгранных): φ1 і φ2. Сума іх роўная π (φ1+ φ2= π). Што тычыцца іх косінус, то іх абсалютныя велічыні роўныя, але яны адрозніваюцца знакамі, то ёсць cos φ1=-cos φ2. Калі ў раўнанні (0) замяніць А, У і З на колькасці -А, -У і -З адпаведна, то раўнанне, якое мы атрымаем, будзе вызначаць гэтую ж плоскасць, адзінае, кут φ у раўнанні cos φ= NN1/|N||N1| будзе заменены на π-φ.
Раўнанне перпендыкулярнай плоскасці
называюцца Перпендыкулярнымі плоскасці, паміж якімі кут роўны 90 градусаў. Выкарыстоўваючы матэрыял, выкладзены вышэй, мы можам знайсці раўнанне плоскасці,перпендыкулярнай іншы. Дапусцім, у нас маюцца дзве плоскасці: Ах+Ву+Cz+D=0 і А¹х+У¹у+З¹z+D=0. Мы можам сцвярджаць, што перпендыкулярнымі яны будуць, калі cosφ=0. Гэта значыць, што NN¹=АА¹+СТСТ¹+СС¹=0.
Раўнанне паралельнай плоскасці
Паралельнымі называюцца дзве плоскасці, якія не ўтрымліваюць агульных кропак.
Умова паралельнасці плоскасцяў (іх ўраўненні тыя ж, што і ў папярэднім пункце) заключаецца ў тым, што вектары N і N¹, якія да іх перпендыкулярныя, коллинеарные. А гэта значыць, што выконваюцца наступныя ўмовы прапарцыйнасці:
А/А¹=У/У¹=З/З¹.
Калі ўмовы прапарцыйнасці з'яўляюцца пашыранымі - А/А¹=У/У¹=З/З¹=DD¹,
гэта сведчыць аб тым, што дадзеныя плоскасці супадаюць. А гэта значыць, што ўраўненні Ах+Ву+Cz+D=0 і А¹х+У¹у+З¹z+D¹=0 апісваюць адну плоскасць.
Адлегласць ад кропкі да плоскасці
Дапушчальны, у нас ёсць плоскасць П, якая зададзена раўнаннем (0). Неабходна знайсці да яе адлегласць ад кропкі з каардынатамі (хₒ,уₒ,zₒ)=Qₒ. Каб гэта зрабіць, трэба прывесці раўнанне плоскасці П у нармальны выгляд:
(ρ,v)=р (р≥0).
У дадзеным выпадку ρ (х,у,z) з'яўляецца радыус-вектарам нашага пункту Q, размешчанай на П, р – гэта даўжыня перпендыкуляра П, які быў выпушчаны з нулявой кропкі, v – гэта адзінкавы вектар, які размешчаны ў кірунку а.
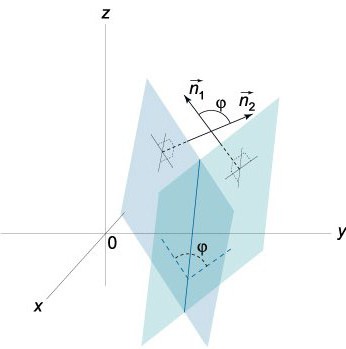
Розніца ρ-ρº радыус-вектара якой-небудзь пункту Q=(х,у,z), які належыць П, а таксама радыус-вектара зададзенай кропкі Q0=(хₒ,уₒ,zₒ) з'яўляецца такім вектарам, абсалютная велічыня праекцыі якога на v роўная адлегласці d, якое трэба знайсці ад Q0=(хₒ,уₒ,zₒ) да П:
D=|(ρ-ρ0,v)|, але
(ρ-ρ0,v)= (ρ,v)–(ρ0,v) =р–(ρ0,v).
Вось і атрымліваецца,
D=|(ρ0,v)-р|.
Цяпер відаць, каб разлічыць адлегласць d ад Q0 да плоскасці П, трэба выкарыстоўваць нармальны выгляд ўраўненні плоскасці, пры гэтым перанесці ў левую частку р, а ў апошнюю замест х,у,z падставіць (хₒ,уₒ,zₒ).
Такім чынам, мы знойдзем абсалютная значэнне атрыманага выразы, то ёсць шуканае d.
Выкарыстоўваючы мову параметраў, атрымліваем відавочнае:
D=|Ахₒ+Вуₒ+Czₒ|/√(А²+²+З²).
Калі зададзеная кропка Q0 знаходзіцца па іншы бок ад плоскасці П, як і пачатак каардынат, то паміж вектарам ρ-ρ0 і v знаходзіцца тупы кут, такім чынам:
D=-(ρ-ρ0,v)=(ρ0,v)-р>0.
У выпадку, калі кропка Q0 сумесна з пачаткам каардынат размяшчаецца па адну і тую ж бок ад П, то які ствараецца кут востры, гэта значыць:
D=(ρ-ρ0,v)=р - (ρ0, v)>0.
У выніку атрымліваецца, што ў першым выпадку (ρ0,v)>р, у другім (ρ0,v)<р.
Датычная плоскасць і яе раўнанне
Датычная плоскасць да паверхні ў пункце дотыку Мº – гэта плоскасць, якая змяшчае ўсе магчымыя датычныя да крывым, праведзеным праз гэтую кропку на паверхні.
Пры такім выглядзе ўраўненні паверхні F(х,у,z)=0 раўнанне датычнай плоскасці ў датычнай кропцы Мº(хº,уº,zº) будзе выглядаць так:
Fх(хº,уº,zº)(х - хº)+ Fх(хº, уº, zº)(у - уº)+ Fх(хº, уº,zº)(z-zº)=0.
Калі задаць паверхню ў відавочнай форме z=f (х,у), то датычная плоскасць будзе апісана раўнаннем:
Z-zº =f(хº, уº)(х - хº)+f(хº, уº)(у - уº).
Скрыжаванне двух плоскасцяў
У трохмернай прасторы размешчана сістэма каардынатаў (прастакутная) Oxyz, дадзены дзве плоскасці П′ і. П″, якія перасякаюцца і не супадаюць. Паколькі любая плоскасць, якая знаходзіцца ў прамавугольнай каардынатнай сістэме, вызначаецца агульным раўнаннем, будзем меркаваць, што П′ і. П″ задаюцца раўнаннямі А′х+У′у+З′z+D′=0″х+У″у+З″z+D″=0. У такім выпадку маем нармаль n′ (А′,У′,′) плоскасці П′ і нармаль n″ (А″,У″,″) плоскасці П″. Паколькі нашы плоскасці не раўналежныя і не супадаюць, то гэтыя вектары з'яўляюцца не коллинеарными. Выкарыстоўваючы мову матэматыкі, мы дадзенае ўмова можам запісаць так: n′≠ n″ ↔ (А′,У′,′) ≠ (λ*А″,λ*У″,λ*З″), λϵR. Няхай прамая, якая ляжыць на скрыжаванні П′ і. П″, будзе пазначацца літарай а, у гэтым выпадку а = П′ ∩ П″.
а – гэта прамая, якая складаецца з мноства ўсіх кропак (агульных) плоскасцяў П′ і. П″. Гэта значыць, што каардынаты любой кропкі, якая належыць прамой а, павінны адначасова задавальняць раўнанні А′х+У′у+З′z+D′=0″х+У″у+З″z+D″=0. Значыць, каардынаты кропкі будуць прыватным рашэннем наступнай сістэмы раўнанняў:
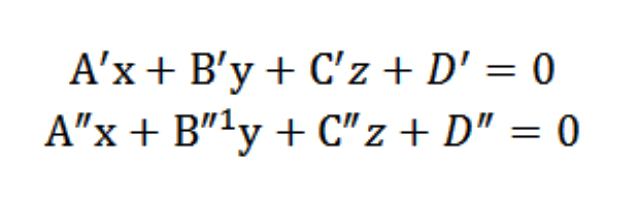
У выніку атрымліваецца, што рашэнне (агульнае) гэтай сістэмы раўнанняў будзе вызначаць каардынаты кожнай з кропак прамой, якая будзе выступаць кропкай перасячэння П′ і. П″, і вызначаць прамую а ў каардынатнай сістэме Oxyz (прастакутнай) у прасторы.
Article in other languages:

Alin Trodden - аўтар артыкула, рэдактар
"Прывітанне, Я Алін Тродден. Я пішу тэксты, чытаю кнігі і шукаю ўражанні. І я нядрэнна ўмею распавядаць вам пра гэта. Я заўсёды рады ўдзельнічаць у цікавых праектах."
Навіны
Кацярына 2: біяграфія імператрыцы. Гісторыя Расіі
Неадназначнай асобай была Кацярына 2 Вялікая – расійская імператрыца нямецкага паходжання. У большасці артыкулаў і фільмаў яна паказана як аматарка прыдворных баляў і раскошных туалетаў, а таксама шматлікіх фаварытаў, з якім...
Іспанская імперыя: апісанне, гісторыя і сцяг
Іспанская імперыя ў часы сваёй магутнасці з'яўлялася адным з найбуйнейшых дзяржаў, якія калі-небудзь існавалі ў свеце. Яе стварэнне неадрыўна звязана з эпохай Вялікіх геаграфічных адкрыццяў, калі яна стала каланіяльнай дзяржавай. ...
Тэматычныя групы слоў: прыклады
Што з'яўляецца адзінкай рускай мовы? Безумоўна, слова. З яго дапамогай мы маем зносіны, перадаем адзін аднаму думкі і перажыванні. У артыкуле разглядаюцца тэматычныя групы слоў, якія дазваляюць класіфікаваць багацце рускай мовы, я...
Самая густанаселеная краіна ў свеце. Манака: цікавыя факты аб княстве
Чалавецтва вельмі нераўнамерна размеркавана па паверхні нашай планеты. Да прыкладу, у невялікім азіяцкім дзяржаве можа пражываць больш людзей, чым на цэлым мацерыку Аўстралія. Дзе ж знаходзіцца самая густанаселеная краіна ў свеце?...
Што такое ледастаў: азначэнне паняцця і яго галоўныя асаблівасці
Рака – гэта не проста вадацёк, які нясецца з гор і ўзвышшаў у мора і акіяны. Гэта даволі складаная экасістэма, своеасаблівы «арганізм», якому ўласцівыя свае асаблівасці і рэжымы. У гэтым артыкуле гаворка пойдзе а...
Псіхалогія колеру ў рэкламе як інструмент продажаў
Індустрыя рэкламы пастаянна расце і развіваецца, аднак нязменным застаецца глыбокае вывучэнне псіхалогіі чалавека, як патэнцыйнага пакупніка. Як прыцягнуць, як звярнуць увагу пакупнікоў менавіта на пэўны від тавару ў шэрагу многіх...





















Заўвага (0)
Гэтая артыкул не мае каментароў, будзьце першым!