Now - 15:12:25
方程式的一面:如何做什么呢? 类型的等式的一面
的空间飞机可以不同的方式设置(一点,并矢量,两点和一矢量,三个点数,等等)。 考虑到这一点,该公式飞机可以有不同的类型。 此外,受到一定的条件,飞机可以平行,垂直的、相互交叉,等等。 和谈在这篇文章。 我们将了解如何获得一个通用公式的一面而不是只。
正式
例如,有一个空间R<子>3,其中有一个直角坐标系统XYZ。 我们定义的矢量α,这将从最初点O通过结束矢量α绘制平面P其是垂直到他。
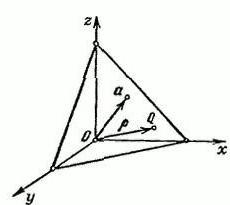
表示由P任意一点Q=(x、y、z)。 半径-矢量的Q点将标志字母R矢量的长度和alpha;等于R=Iα我和故=(因为α因为&测试;cosγ).
这是一个矢量单元,旨在作为方向的矢量的α. α,&测试;和γ家庭债务还清的角度之间形成一种矢量偏差和积极的方向的轴空间的x、y、z,分别。 突起的任何点上QϵП故矢量是一定的,这等于:(p,故)=p(p≥0).
指定的公式是有道理的,当R=0. 唯面P在这种情况下,将交叉点(和alpha;=0),这是起源的矢量单元的故解雇O点垂直于P,尽管其方向,这意味着故矢量是确定上签署。 上述方程式的我们的飞机P表示矢量形式。 但是,在坐标它看起来是这样的:
推荐
在本文中,我们将重点放在副词和语法特性副词。 因此,我们首先需要了解什么是个副词。的一个副词,作为一项规则,被理解为一个独立的部分讲话,表示一定的注册行动,签署各国,至少-这个问题。 有关的例子是搭配的动词-副词:睡眠、爱、快速运行,眼睛的权利,等等。特的作用是什么一个副词在一个句子? 有关的句子,该句话-副词,作为一项规则,作为的情况。 更不在该提案可以满足副词,它作为一个定义。 但是,这种现象发生时的副词是毗邻的名词。 经常提案满足短语的一个词是一个副词。 的方言也存在其他几种语言,但在其他...
的现代心理学不再是一个秘密的事实,该人在进程的发展和形成经过几个阶段,彼此不同的级别:物;的心理;精神,和知识产权的发展。换句话说,该进程为增长和发展是伴随着某些变化在运作的机构,有助于区分一个阶段从另一个。 和这些变化具有很强的关系,与年龄。 这个概念被称为年龄期间。中的作品的许多学者和图从心理学已审查的各个阶段的年龄分期:弗洛伊德,L.S.维果茨基D.Elkonin. 在这篇文章,更详细地将被认为是什么年龄分期Elkonin D.B.作为最受欢迎俄罗斯现代心理学。理论的俄罗斯科学家是基于这样...
每一个企业有一个特定系统的组织支付的劳动潜力的雇员。 它可能有几个部分组成的或含有仅仅一小部分工资的形式的薪水。,以避免冲突,在工作场所,这是必要的激励员工,以增加生产力在工作场所通过的合理组织的工资,其中之一是关税的免费系统。实体免关税系统的劳动付款在企业一是开发了一个系统,其实质是,工资取决于每个雇员的性能和其工作效力和工作,他的团队作为一个整体。 在推进工作人员不知道有关金额,将发给他在完成。的特殊特征的免关税工资的系统是能够激励员工,以提高其性能。免关税系统是一种确定的薪酬的雇员的公司受...
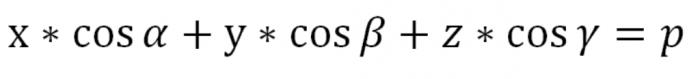
这里,R大于或等于0。 我们找到了等式的一架飞机在空间在正常形式。
一般式
如果方程式中的坐标乘以任何数量不为零,我们将获得的公式,这是相当于指定相同的飞机。 它将是这样的:
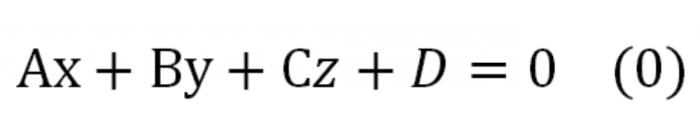
这里A、b、C家庭债务还清这是数量的同时不同于零。 这个公式被称作等式的一个平面的一般形式。
方程式飞机。 特殊情况下
的方程式中的一般形式可以是修改附加条件。 考虑到一些他们。
假设这一系数等于0。 这意味着,鉴于飞机是平行的牛轴。 在这种情况下,该公式将发生变化:武+Cz+D=0.
同样,该公式将会改变以下条件:
- <李>第一,如果=0,则的公式将改变,以斧头+Cz+D=0,这表明平行轴Oy。<李>第二,如果C=0,该公式转化为Oh+武+D=0,这将谈论的并行给轴盎司。<李>第三,如果D=0,该公式将会看起来像斧+武+Cz=0,这将意味着,这架飞机相交O(原点的坐标)。<李>第四,如果A=B=0,该公式将会改变来Cz+D=0,这将证明是一个平行氧.<李>第五,如果B=C=0式变为ax+D=0,这意味着平行Z.<李>第六,如果一=C=0,该公式将采取的形式vu+D=0,即将报告的平行Oxz.
形式段
的情况下,当号A、b、C、D零,该公式(0)可以如下:
X/a+y/b+z/C=1
在这一=-D/A、b=-D/C=-D/S.
得到的公式飞机在分段。 应当指出,这种机会横轴牛点坐标(a,0,0),哦,家庭债务还清(0,b,0),并兹家庭债务还清(0,0,C).
定的方程式x/a+y/b+z/C=1中很容易想象平面上的位置相对于定义的坐标系统。
的坐标线矢量
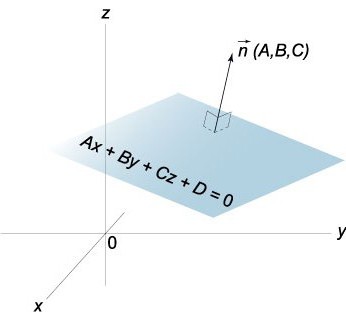
线矢量n面的P已经坐标的系数一般公式的这架飞机,那就是,n(A,b,C).
确定坐标的正常n,这是不够知道本公式给出的飞机。
时使用的公式分段,其有形式x/a+y/b+z/C=1,因为在一般的公式,我们可以编写标的任何正常的矢量的一定面:(1/1/b+1/C)。
值得注意的是,正常的矢量有助于解决各种各样的问题。 最常见的任务,其中包括在证明垂直度或表面平行,任务是寻找的角度之间的飞机或角度之间的飞机和直线。
形式的飞机的据点的坐标和正常的矢量
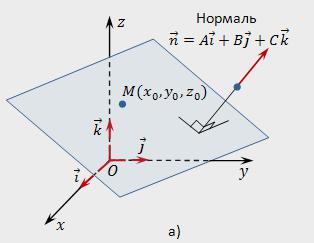
的一个非零矢量n垂直的指定的平面内,被称为正常的(通常的)为给予飞机。
假设,在协调空间(直角坐标系统)Oxyz是规定:
- <李>点莫与坐标(xₒ,yₒ,zₒ);<李>零矢量n=A*i+A*j+C*k.
,我们需要编写的公式飞机将通过的一点是垂直的正常n.
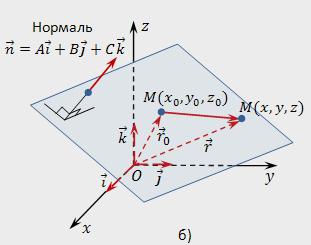
在的空间,我们选择任意一点,并表示它M(x,z)。 让半径-矢量的任何一点M(x、y、z)r=x*i+y*j+z*k和半径矢量的一点莫(xₒ,yₒ,zₒ)家庭债务还清rₒ=xₒ*i+yₒ*j+zₒ*k。 M点属于指定的飞机,如果矢量的国际移徙组织将垂直的矢量。 写信的条件的正交使用点的产品:
[IOM,n]=0.
由于M=研庭债务还清rₒ,矢量的公式的一面会是这样的:
[研庭债务还清rₒ,n]=0.
这个方程式可以有不同的形状。 为此目的,性质的标产品,并且是转向左侧的公式。 [研庭债务还清rₒ,n]=[r,n]家庭债务还清[rₒ,n]。 如果[rₒ,n]表示的C,我们得到以下等式:[r,n]家庭债务还清=0或[r,n]=C,其中表示坚定不移的预测正常的矢量的半径矢量的特定点,属于飞机。
现在有可能以协调的记录矢量程的我们的飞机[研庭债务还清rₒ,n]=0. 由于r家庭债务还清rₒ=(x家庭债务还清xₒ)*i+(u家庭债务还清yₒ)*j+(z家庭债务还清zₒ)*k和n=A*i+A*j+C*k,我们有:
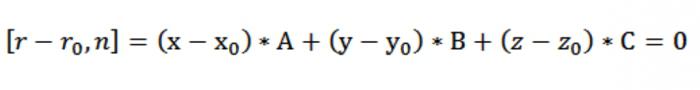
因此,我们已经形成的公式飞机通过点垂直于正常n:
*(x xₒ)+V*(u家庭债务还清yₒ)C*(z家庭债务还清zₒ)=0.
形式的飞机根据两点的坐标和矢量,共线的飞机
我们定义的两个任意点M&总理;(x&素;t&素;z&素;)和M&总理;(x&素;t&素;z&素;)和一矢量的一种(a&总理;以及&素;和").
现在我们可以写下公式给出的飞机,这将通过点M&总理;M&素;和任何M点坐标(x、y、z)平行一定的矢量。
载于M&总理;M={x-x&总理;;y-y&素;;z&总理;}M&总理;M={x&总理;x&素;;u&素;-y&总理;z&总理;z&总理;}必须共面的矢量=(a&总理;以及&素;和"),这意味着(M&素;M&素;M)=0.
因此,我们式的飞机在空间就是这样的:
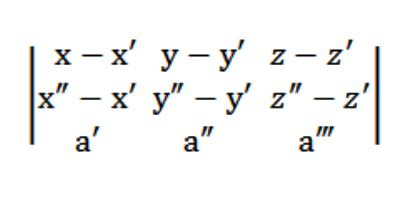
形式的飞机交的三点
假设我们有三点:(x&素;t&素;,z&素;)、(x&素;t&素;z&素;)、(x",y",z"),不属于一个直线。 你必须写信的方程的平面通过指定的三点。 该理论的几何声称,这样的飞机确实存在的,除了她是唯一的. 由于这架飞机相交的点(x&素;t&素;z&素;),形式其公式如下:
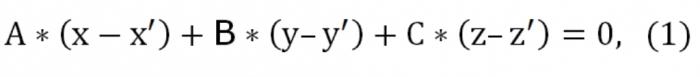
这里的一,b,C不同于零,在同一时间。 也给出面交两点:(x&素;t&素;z&素;)和(x",y",z")。 在这方面应该进行这样的条件:
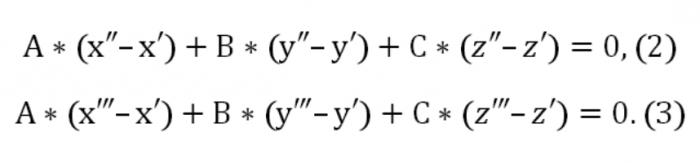
现在我们可以写下一均质的等式系统(线性)与未知u,v,w:
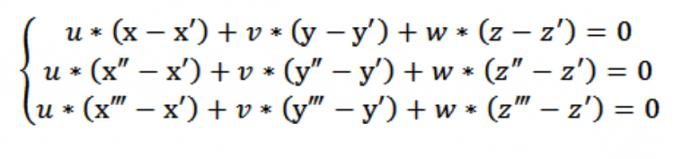
在我们的情况下,x、y或z行为的任意一点,满足公式(1)。 给定的公式(1)和公式(2)和(3)该系统的公式显示在图上所述,满足矢量N(A,b,C),这是非微不足道的。 这是因为决定因素,这个系统等于零。
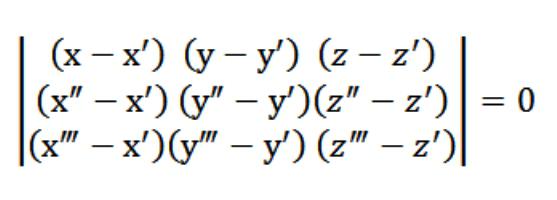
公式(1),我们做到了,这是公式飞机。 3点肯定的是,它很容易检查。 为此您需要奠定了我们的关键要素,在第一行。 现有的属性的决定因素,它遵循我们的飞机同时相交叉的三个原定点(x&素;t&素;z&素;)、(x&素;t&素;z&素;)、(x",y",z")。 所以我们决定的任务集中在我们面前。
之间的两面角飞机
的两面角是一个空间几何图形成由两个半的飞机起源于相同的线。 换句话说,这部分空间,这是限制这些半的飞机。
假设我们有两架飞机用以下等式:
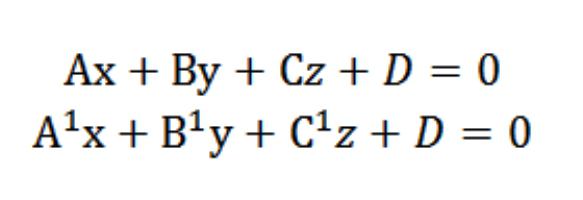
我们知道,矢量N=(A、b、C)和N¹=(A¹、¹;¹) 都是垂直根据指定的飞机。 在这方面,本角度与披矢量之间N N¹等的角度(蝴蝶),这是位于这些飞机。 标产品具有形式:
NN¹=|N||N¹|cos&皮;
只是因为
因为&皮;=NN¹/|N||N¹|=(a¹+W¹+SS¹)/((√(A²+B²+S²))*(√(A¹)²+(V¹)²+(S¹)²)).
它是足够的注意,0≤&皮;≤π.
实际上两架飞机,相互交叉,形成两个角度(蝴蝶):&皮;<子>1和&皮;<子>2. 总和他们是平等的,π(&皮;<子>1+&皮;<子>2=π). 至于其余弦,他们的绝对值是相等的,但是他们在不同的迹象,那就是,因为&皮;<子>1=-因为&皮;<子>2. 如果公式(0)替换A、b和C号A、b和C分别,则等式,我们会确定同一平面,唯一的角度和披;在公式,因为&皮;=NN1/|N||N1|将取代π-&皮;.
式的垂直的平面
称为垂直的平面之间的夹角90度。 使用的材料提出上述,我们可以找到公式的一面垂直的。 我们说我们有两架飞机:斧+武+Cz+D=0¹x+V¹;我+C¹;z+D=0. 我们可以说,他们将垂直的,如果因为&皮;=0. 这意味着NN¹=AA和sup1;+BB¹+SS¹=0.
方程的平行
称为两个平行的飞机,其不包含共同点。
的条件并行的飞机(他们的方程式是相同的,在前一段)的是,矢量N N¹;它们是垂直的,直排。 这意味着以下条件下的相称性:
A/A¹=I/¹=与¹.
如果条件相称的适用范围延伸至A/A¹=I/¹=与¹=DD¹
这表明数据的飞机都是一样的。 这意味着ax+武+Cz+D=0¹x+V¹;我+C¹;z+D¹=0描述了同样的飞机。
的距离飞机从一个点
假设我们有一个平P其是由等式(0). 你需要找之间的距离有点坐标(xₒ,yₒ,zₒ)=Qₒ. 要做到这一点,需要给予等式中的飞机在一个正常的形式:
(&罗;v)=p(p≥0).
在这种情况下&罗;(x、y、z)矢量半径的点问,位于P、研庭债务还清是的长度的垂直P,这是从零点,v家庭债务还清是一个矢量单元,这是位于的方向。
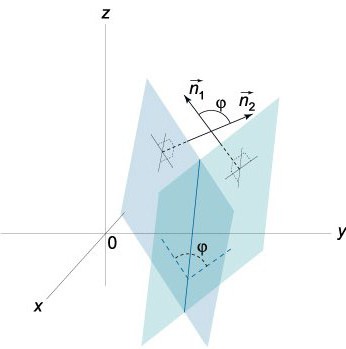
罗;-&罗;º;矢径的任何一点Q=(x、y、z)属于P半径-矢量的一个指定点Q<子>0=(xₒ,yₒ,zₒ) 是这样一种矢量,绝对价值的投影,在v等于距离d,这需要发现从Q<子>0=(xₒ,yₒ,zₒ),P:
D=|(&罗;-&罗;0,v)|,但
(&罗;-&罗;0,v)=(&罗;v)家庭债务还清(&罗;0,v)=p家庭债务还清(&罗;0,v).
因此,
D=|(&罗;0,v)-R|.
现在你可以看到来计算距离,从d Q<子>0的P面,有必要使用正常的方程式中的一架飞机,转移到左边R,最后是x、y、z替代(xₒ,yₒ,zₒ).
因此,我们看到的绝对值得表达,即,所需d.
使用的语言获得的参数是显而易见的:
D=|被遗弃弹药+a武奥+Czₒ|/&radic;(A&su p2+在及su p2+C&su p2).
如果指定的一点是Q<子>0是在另一侧的平P如原产地之间,矢量&罗;-&罗;0和v是一个钝角,从而:
D=-(&罗;-&罗;0,v)=(&罗;0,v)研gt;0.
的情况下,当一点Q<子>0与原籍国的坐标位于同一边的P,创造角尖锐,那就是:
D=(&罗;-&罗;0,v)=R-(&罗;0,v)>0.
的结果是,在第一种情况下(&罗;0,v)>R在第二(&罗;0,v)<R.
相切的平面及其等式
在飞机上的表面相切点Mº家庭债务还清 这是面包含所有可能的切线的曲线,绘制通过这一点的表面上。
在这种形式的表面上的F(x、y、z)=0式的相切的平面在切点Mº;(xº、uº,zº)将这样的:
F<子>X(xº、uº,zº)(x-xº)+F<子>X(xº、uº,zº)(u-uº)+F<子>X(xº、uº,zº)(z-zº)=0.
如果指定一个表面在一个明确的形式z=f(x,y),相切的平面将要描述的公式:
Z-zº=f(xº、uº)(x-xº)+f(xº、uº)(u-uº).
交的两架飞机
在三维空间系统的坐标(矩)Oxyz,鉴于两架飞机的P&总理;P&总理;,其相互交叉和不一致。 因为任何平面直角坐标系统,是通过确定一般性公式,我们认为P&总理;P&素;定义的方程式中的一个&总理;x+V&总理;在+M&总理;z+D&素;=0&总理;x+V&总理;在+M&总理;z+D&素;=0. 在这种情况下,我们有一个正常n&素;(I&总理;在&素;S&素;)面的P&总理;以及正常n&素;(I&总理;在&素;S&素;)面的P&素;. 由于我们的飞机不是平行的并不重合,那么这些矢量不直排。 使用数学的语言,我们这个条件可以写为:n&素;&ne;n&素;&harr;(A&总理;在&素;S&素;)&网元;(&lambda;*与&素;,&lambda;*在&素;,λ*C&素;),λϵR. 我们该直线的位于交叉点的P&总理;P&素;将由相信,在这种情况下,=P&素;&盖;N&素;.
和家庭债务还清的视频由设置的所有要点(总数)的飞机的P&总理;P&素;. 这意味着坐标的任何一点属于一条直线,并且必须同时满足公式的一个&总理;x+V&总理;在+M&总理;z+D&素;=0&总理;x+V&总理;在+M&总理;z+D&素;=0. 因此,坐标点将是私人的解决方案的以下系统的方程式:
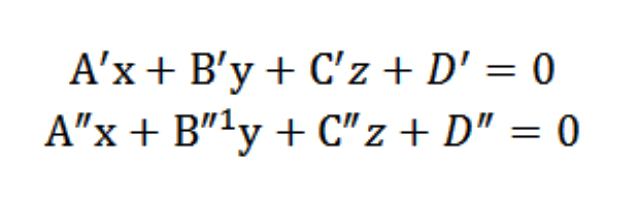
在结束时,事实证明,解决(公共)的这个系统的方程将确定各点的坐标, 这将作为交叉点的P&总理;P&素;并确定该线以及在坐标系统Oxyz(矩)在空间。
Article in other languages:

Alin Trodden - 文章作者、编辑
"你好,我是艾琳*特罗登。 我写文章,看书,寻找印象。 我也不擅长告诉你这件事。 我总是乐于参与有趣的项目。"
相关新闻
含糊不清的个性是2凯瑟琳大家庭债务还清;一个俄罗斯女皇,德国的起源。 大多数文章和电影她是示,作为一个情人的臣子的球和豪华的厕所,以及许多人收藏,与她曾经非常接近。不幸的是,很少有人知道她很聪明,光明和有才能的组织者。 它是一个不争的事实,因为政治变化,发生在多年的她统治时期,属于开明的绝对论。 此外,许多改革影响到公众生活的国家,是另一个证明的独创性,她的个性。[rek1]起源2凯瑟琳的传记这是如此奇怪和不寻常的,出生在2月(21个月)1729年在德什切...
西班牙帝国在它的力量是其中一个最大的国家曾经存在的世界。 它的建立是密切相关,与时代的伟大的地理发现,当它成为一个殖民地的权力。 几个世纪的标志西班牙帝国经发展了一个广阔的领土,位于这两者在欧洲和在亚洲、非洲、美洲和大洋洲。的外表状态大多数历史学家认为,西班牙,作为帝国开始了它的存在,在十五世纪晚期,当时在1479签署了《卡斯蒂利亚-拉贡联盟,导致在合并的土地的统治伊莎贝拉我的天主教和费迪南德II。 有趣的是,作为配偶,君主统治其领土,因为他们请,但是作为...
有什么单元的俄罗斯语言? 当然,这个词。 有了它,我们沟通,分享彼此的想法和感受。 该文讨论了专题小组的话,这类丰富的俄罗斯语言,包括在其文学词典的150多万名词、动词和形容词。词俄罗斯语言学研究,不采取行动,而不迹象,和所说的话打电话给他们。 他们有两个值:文法(责任的结束词).词汇(基础).了解什么是专题小组的话,重点关注的第二段。 词汇的含义,家庭债务还清它的内容,或者在历史上载于人之思想,相关之间的声音壳和这一现象的现实,旨在根据法律的语法。 男人...
人类是非常不均匀地分布在表面上的我们的星球。 例如,在一个亚洲小国家可以容纳更多人,比整个非洲大陆的澳大利亚。 哪里是人口最稠密的国家在世界吗? 什么使得它有趣的事吗? 让我们来面对它。 概念的人口密度:人口最稠密的国家,在世界下的人口密度平均数的居民每单位面积(往往家庭债务还清1平方公里). 这一指标不同,在不同国家和地区的世界。 因此,在大城市,它可以达到几千人,每1平方公里,在其他地区对地球运行的危险没有看到一个活生生的灵魂的许多几十甚至几百公里。 ...
河家庭债务还清;它不只是流着来自山区和丘陵在海洋和海洋。 这是一个非常复杂的生态系统,是一种目的身体号;,其特点是通过它自己的特点和模式。 在本文中,我们将重点放在温和冰制度的河流。什么是冰? 定义的这个和其他一些地理条件,你会发现在我们的文章。 什么时候和为什么没有河流成为所复盖的冰壳? 什么阶段的冰制度孤立的科学家?冰制度河和它的阶段。 什么是冰?的定义的一个概念是重要的综合研究和合理利用自然资源。 在这种情况下,我们感兴趣的代表河家庭债务还清一个复杂...
什么是一个传统的诗歌? 什么是历史的民俗,特别是这种风格? 让我们试试一起寻找这些问题的答案。介绍俄罗斯传统的诗歌,他的出现欠的民间艺术。 民间传说是口头的民间艺术。 它反映了集体创造性活动的人为特征,他的理想、信仰、生活方式。类型仪式民间诗歌的创建是通过许多世纪。 史诗般的笑话,以及各种故事、民谣传说,一切都交给下一代又一代。 在这种口活动所载历史的信息有关的传统和生活的人。[rek1]传统的诗歌被转移到音乐,所有的戏剧和音乐. 他们能明白什么是生命的普...






















评论 (0)
这篇文章没有评论,是第一!