Now - 20:58:05
A equação do plano: como fazer? Tipos de equações do plano
Em um espaço plano, você pode definir diferentes formas (um ponto e um vetor, dois pontos e um vetor a, com três pontos e др.). É com isso em mente, a equação do plano podem ser de vários tipos. Também está sujeito a certas condições do plano podem ser paralelas, перпендикулярными, sobrepostos e т. д. e falar Sobre isso neste artigo. Aprendemos a ser de equação geral do plano e não só.
Normal equação
Digamos que há espaço R3, que tem retangular координатную sistema XYZ. Definimos um vetor α, que será lançado a partir de um ponto inicial О. Através da extremidade do vetor α traçar um plano de N, que lhe é perpendicular.
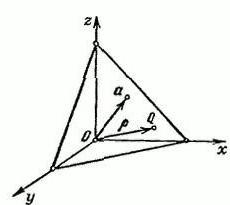
Denotar por P um ponto arbitrário Q=(x,y,z). O raio vetor do ponto Q assinaremos a letra р. neste comprimento do vetor α é igual a p=IαI e Ʋ=(cosα,cosβ,cosγ).
Este É o único vetor, que é direcionado para o lado, como vector α. α, β e γ ã o os ângulos que se formam entre o vetor de Ʋ e sentidos positivos dos eixos do espaço x, y, z, respectivamente. A projeção de um qualquer ponto de QϵП no vetor Ʋ é um valor constante que é igual a p: (p,Ʋ) = p(p≥0).
Indicado a equação tem sentido quando p=0. A única coisa, o plano de N neste caso, vai atravessar a ponto De (α a=0), que é o início de coordenadas, e um único vetor de Ʋ, lançado a partir de um ponto Sobre, será perpendicular à análise, apesar de sua direção, o que significa que o vetor Ʋ determinada com precisão até a marca. Anterior, a equação é a equação de nosso plano N, pronunciado em forma de vetor. E aqui em coordenadas de sua vista será assim:
Mais:
A história do desenvolvimento da tecnologia de computação
Os primeiros dispositivos de computação foram os próprios dedos de uma pessoa. Quando a ferramenta foi suficiente, no curso de iam pedras, galhos, conchas. Dobrando-se de um conjunto de dezenas, depois centenas, o homem aprendeu a contar e usar as fe...
O impulso nervoso, a sua conversão e o mecanismo de transmissão
O sistema Nervoso humano atua como uma espécie de coordenador no nosso corpo. Ela passa o comando do cérebro musculatura, órgãos, tecidos e processa os sinais de longo alcance deles. Como uma espécie de suporte de dados, é usado o impulso nervoso. O ...
Canal do panamá: um ano, a abertura oficial do objecto e a sua importância histórica
Durante séculos, a humanidade tenta recriar condições naturais da Terra, com o objetivo de receber quaisquer benefícios. Um desses casos, a adaptação é do canal do Panamá, o ano, a abertura oficial deste objeto foi marcado por um evento, повлиявшим p...
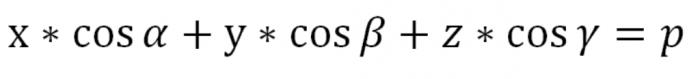
Aqui P maior ou igual a 0. Nós encontramos a equação do plano no espaço na forma normal.
Equação Geral
Se a equação em coordenadas de se multiplicar em qualquer número que não é igual a zero, obtemos uma equação equivalente à dada, indicando a maior lisura. Ele terá o seguinte formato:
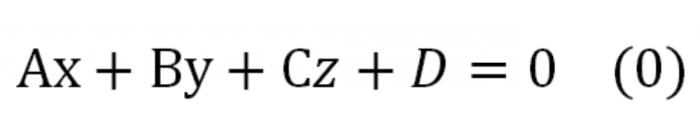
Aqui, Em s ã o número, simultaneamente, diferente de zero. Esta equação é conhecido como equação de plano de aspecto geral.
Equações de planos. Casos especiais
A Equação na forma geral pode evoluir se tiver mais condições. Vejamos algumas delas.
Por exemplo, Suponha que o coeficiente E é igual a 0. Isso significa que esse plano está paralela ao determinado eixo Ox. Neste caso, o tipo de equação será alterado: Wu+Cz+D=0.
Da mesma forma vista equação irá mudar e se as condições seguintes:
- Primeiro, se A=0, então a equação de mudar o Ah+Cz+D=0, o que indicaria paralelo ao eixo do amp-op.
- Em segundo lugar, se c=0, então a equação é convertido em Ah+Wu+D=0, que vai falar sobre a concorrência a um determinado eixo Oz.
- Em terceiro lugar, se D=0, a equação será parecido com Ah+Wu+Cz=0, o que significa que o avião cruza-se Sobre o (a origem).
- Em quarto lugar, se A=B=0, então a equação muda para Cz+D=0, o que vai provar o paralelismo ao Oxy.
- Em quinto lugar, se B=C=0, então a equação será o Ah+D=0, o que significa que o plano a Oyz está paralela.
- Em sexto lugar, se A=C=0, então a equação de adquirir vista Wu+D=0, ou seja, terá de informar a concorrência Oxz.
O Tipo de equação, em cortes
Em caso de quando os números A, b, c, D são diferentes de zero, vista a equação (0) pode ser a seguinte:
X/ + /b + z = 1,
Em que e = -D/E, b = -D/A, com a = -D/С.
Recebemos finalmente a equação do plano de cortes. Vale ressaltar que este plano vai cruzar o eixo Ox no ponto de coordenadas (a,0,0), Ou – (0,b,0) e Onças – (0,0,c).
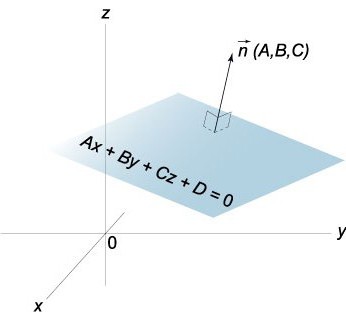
Dada a equação x/ + /b + z = 1 é fácil de visualizar pelos planos relativamente a determinado sistema de coordenadas.
As Coordenadas do vetor normal
O vetor Normal n ao plano P tem coordenadas, que são os coeficientes a equação geral deste plano, ou seja, n (A,b,c).
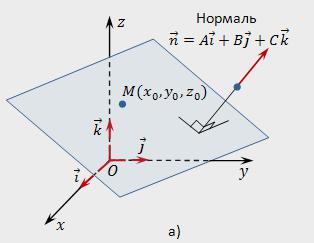
Para determinar as coordenadas de normal n, é o suficiente para saber equação determinado plano.
Ao utilizar a equação em cortes, que tem a aparência de x/ + /b + z = 1, como e quando utilizar a equação geral, pode gravar as coordenadas de qualquer normal do vetor set avião: (1/a + 1/b + 1/c).
Vale ressaltar que o vetor normal ajuda a resolver uma variedade de tarefas. O mais comum são as tarefas que ocorrem na prova perpendicularidade ou de concorrência dos planos, a tarefa de encontrar os ângulos entre os planos, ângulos entre planos e retas.
O Tipo de equação do plano de acordo com as coordenadas de um ponto e normal do vetor
Zero de um vetor de n, perpendicular determinado plano, chamado de normal (нормалью) para um determinado plano.
Por exemplo, Suponha que no координатном espaço retangular de coordenadas o sistema Oxyz feitas:
- Ponto de Мₒ com coordenadas (хₒ,уₒ,zₒ);
- Zero vetor n=E*i+*j+k*.
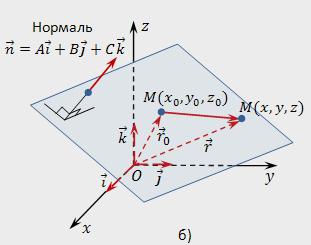
, você Precisará criar uma equação do plano, que será realizada através de um ponto de Мₒ perpendicular a normal n.
No espaço de escolher qualquer ponto arbitrário e nós deixamo-la M (x, y,z). Deixeo raio-vetor qualquer ponto M (x,y,z) é r=x*i+y*j+z*k, e o raio vetor do ponto de Мₒ (хₒ,уₒ,zₒ) – rₒ=хₒ*i+уₒ*j+zₒ*k. O ponto M é pertencer a um determinado plano, se o vetor МₒМ vai está perpendicular ao vetor n. Vou escrever a condição de ортогональности usando escalar obras:
[МₒМ, n] = 0.
Uma Vez МₒМ = r–rₒ, uma equação vetorial do plano do olhar seria assim:
[r – rₒ, n] = 0.
Esta equação pode ter uma forma diferente. Para isso, são utilizadas as propriedades de escalar obras, e converte o lado esquerdo da equação. [i – rₒ, n] = [r, n] – [rₒ, n]. Se [rₒ, n] indicar como, obtemos a seguinte equação: [r, n] – com a = 0 ou a [p, n] = a, que expressa a permanência das projeções para o vetor normal raio-vetores conjunto de pontos que pertencem ao plano.
Agora você pode obter координатный tipo de registro vetorial da equação de nosso plano [r – rₒ, n] = 0. Porque r–rₒ = (x–хₒ)*i + (y–уₒ)*j + (z–zₒ)*k e n = E*i+*j+*k, temos que:
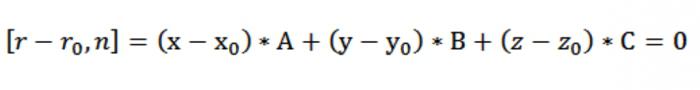
Sai, temos образовывается a equação do plano que passa através de um ponto perpendicular ao normal n:
*(x - хₒ)+*(– уₒ)*(z–zₒ)=0.
O Tipo de equação do plano de acordo com as coordenadas de dois pontos e de um vetor, коллинеарного plano
Temos dois pontos arbitrários M′ (x′,′,z′) e M″ (x″,″,z″), bem como o vetor e (e′,e″ e").
Agora somos capazes de elaborar uma equação de determinado plano, que será realizada através de um ponto disponível de M′ e M″ e também todo ponto de M, com coordenadas (x,y,z), paralelamente a um determinado vetor e.
Apesar de vetores de M′M={x-x′;y-y′;z-z′} e M″M={x″-x′;″-′;z″-z′} deve ser компланарными com vetor a=(e′,e″ e"), e isso significa que (M′M, M″M, a)=0.
Então, nossa equação do plano no espaço ficaria assim:
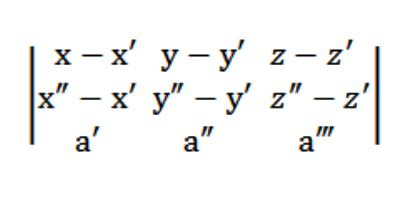
Vista equação de avião, uma travessa de três pontos
Por exemplo, Suponha que temos três pontos: (x′,′,z′), (x″,″,z″), (x",y", "z"), que não pertencem à mesma reta. Você precisa escrever uma equação do plano que passa através definidos três pontos. A teoria da geometria afirma que esse tipo de plano realmente existe, isso é só ele o único e inimitável. Porque esse avião cruza o ponto (x′,′,z′), vista a sua equação é a seguinte:
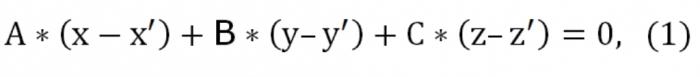
Aqui, diferente de zero ao mesmo tempo. Também definido o plano de cruza-se ainda dois pontos: (x″,″,z″) e (x",y", "z"). Por este motivo, devem ser executados esse tipo de condição:
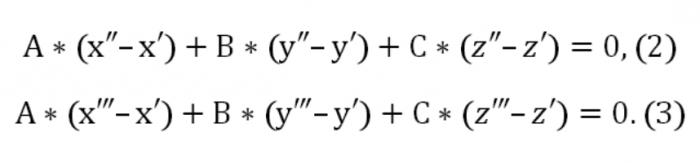
Agora podemos formar uma massa homogénea sistema de equações (linear) com desconhecidos, u, v, w:
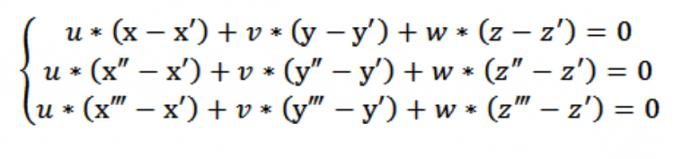
No nosso caso x,y ou z atua arbitrária de partida, que satisfaz a equação (1). Considerando a equação (1) e o sistema de equações (2) e (3), sistema de equações, indicada na figura acima, satisfaz o vector N (A,b,c), que é trivial. Precisamente porque o determinante deste sistema é igual a zero.
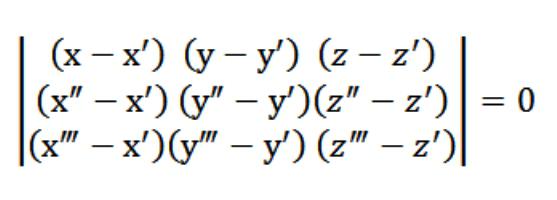
A Equação (1), que nós temos, é a equação do plano. Através de 3 pontos, ela só passa, e isso é fácil de verificar. Para isso, é necessário colocar o nosso determinante de todos os elementos que estão na primeira linha. A partir de propriedades existentes determinante que se segue, que o nosso plano, simultaneamente, cruza três originalmente especificados de um ponto (x′,′,z′), (x″,″,z″), (x",y", "z"). Ou seja, nós decidimos colocado diante de nós a tarefa.
Двухгранный o ângulo entre os planos
Двухгранный ângulo é uma figura geométrica espacial, formado a dois полуплоскостями, que se originam a partir de uma única linha. Em outras palavras, é parte do espaço que é limitado полуплоскостями.
Suponhamos que temos dois planos com as seguintes equações:
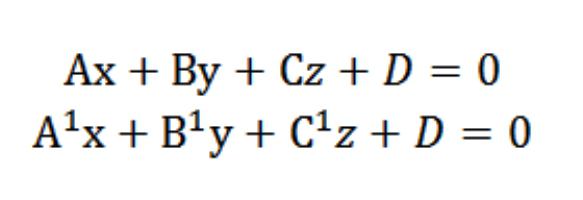
Sabemos que os vetores N=(A,b,c) e N¹=(E¹¹¹) perpendicular de acordo com aviões. Neste contexto, o ângulo φ entre os vetores N e N¹ igual canto (двухгранному), que está entre os planos. O produto escalar é:
NN¹=||N / |N¹|cos φ,
é porque
Cosφ= NN¹/|N||N¹|=(АА¹+ВВ¹+СС¹)/((√(А²+В²+С²))*(√(А¹)²+(В¹)²+(С¹)²)).
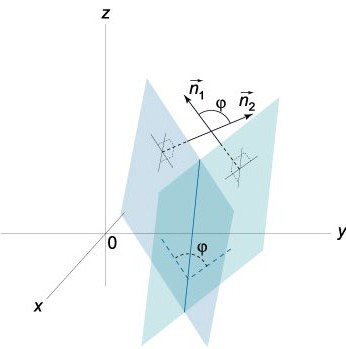
O Suficiente para considerar que 0≤φ≤π.
Na verdade, os dois planos que se cruzam formam ângulo de dois (двухгранных): φ1 e φ2. A soma deles é igual a π (φ1+ φ2= π). No que diz respeito a sua co-seno, seus valores absolutos são iguais, mas são diferentes eles são registradas, ou seja, cos φ1=-cos φ2. Se na equação (0) substituir o Bem, e Com o número -E-e -s, respectivamente, então a equação que recebemos, é identificar esse mesmo plano, a única coisa ângulo φ na equação cos φ= NN1/|N||N1| será substituído por π-φ.
A Equação perpendicular ao plano
Перпендикулярными são chamados de planos, entre os quais o ângulo é igual a 90 graus. Usando o material indicado acima, podemos encontrar a equação do plano,uma perpendicular à outra. Suponha que você tem dois planos: Ah+Wu+Cz+D=0 e E¹x+¹+¹z+D=0. Podemos afirmar que перпендикулярными eles vão se cosφ a=0. Isso significa que NN¹=AA¹+BB¹+SS¹=0.
A Equação do plano paralelo
Em Paralelo, são chamados de os dois planos, que não contêm pontos em comum.
A Condição de concorrência dos planos (equação é o mesmo que no item anterior) é que os vetores N e N¹, que lhe são perpendiculares, коллинеарные. E isso significa que as seguintes condições forem verdadeiras proporcionalidade:
A/E¹=Na/Em¹=Com/S¹.
Se as condições de proporcionalidade são avançados - Em/Em¹=Na/Em¹=Com/S¹=DD¹,
Isso indica que o plano de dados coincidem. E isso significa que a equação Ah+Wu+Cz+D=0 e E¹x+¹+¹z+D¹=0 descrevem um plano.
A Distância até o plano do ponto de
Suponhamos que temos um plano de N, que é definida pela equação (0). A necessidade de encontrar para ela, a distância de um ponto com coordenadas (хₒ,уₒ,zₒ)=Qₒ. Para fazer isso, você precisa levar a equação do plano N ao normal tipo:
(ρ v,v)=p (p≥0).
Neste caso, ρ (x,y,z) é o raio-vetor de nosso ponto Q, situado em N, p – é o comprimento da perpendicular N, que foi lançado a partir do ponto zero, v ã o único vetor que está na direção do bem.
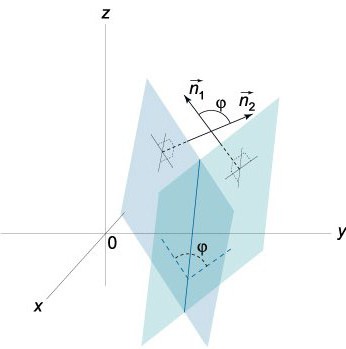
A Diferença ρ-ρº o raio-vetor de algum ponto Q=(x,y,z), pertencente N e o raio vetor de um determinado ponto Q0=(хₒ,уₒ,zₒ) é o vetor que o valor absoluto da projeção que v é igual a uma distância d, que precisa de encontrar a partir de Q0=(хₒ,уₒ,zₒ) até N:
D=|(ρ-ρ0,v)|, mas o
(ρ-ρ0,v)= (ρ v)–(ρ0,v) =p–(ρ0,v).
Assim, verifica-se
D=|(ρ0,v)-p|.
Agora, visível, para calcular a distância d do Q0 até o plano de N, você precisa usar o tipo normal equação do plano, quando este transferir na parte esquerda do p, e, por último, em vez de x,y,z substituir (хₒ,уₒ,zₒ).
Desta forma, vamos encontrar o valor absoluto da derivada da expressão, isto é, a palavra de d.
Usando a linguagem de parâmetros, obtém-se o óbvio:
D=|Ахₒ+Вуₒ+Czₒ|/√(E²+²+²).
Se a um ponto Q0 está do outro lado do plano de N, como a origem, então, entre o vetor ρ-ρ0 e v encontra-se um ângulo obtuso, portanto:
D=-(ρ-ρ0,v)=(ρ0,v)-p>0.
Em caso de quando o ponto Q0 junto com o início de coordenadas localiza-se a mesma direção de N, então é criado um ângulo agudo, ou seja:
D=(ρ-ρ0,v)=p (ρ0, v)>0.
O resultado é que, no primeiro caso (aρ0,v)>p, o segundo (ρ0,v)<р.
Plano Tangente e a equação
Sobre o plano à superfície no ponto de toque de Mº ã o plano que contém todos os possíveis tangentes às curvas, realizada por esse ponto na superfície.
Neste tipo de equação da superfície F(x,y,z)=0 a equação do plano tangente a tangente de um ponto de Mº(xºº,zº) ficaria assim:
F(xºº,zº)(x - xº)+ F(xºº, zº)(y - yº)+ F(xºº,zº)(z-zº)=0.
Se você definir a superfície de forma explícita z=f (x,y), então a tangente plano será descrita pela equação:
Z-zº =f(xºº)(x - xº)+f(xºº)(y - yº).
A Interseção de dois planos
No espaço tridimensional, está o sistema de coordenadas (retangular) Oxyz, são dadas duas plano de P′ e N″ que se cruzam e se não coincidirem. Como qualquer plano, localizada na retangular de coordenadas de um sistema, determinada pelo equação, vamos supor que N′ e N″ são definidas equações E′x+′+′z+D′ a=0 e E″x+″+″z+D″ a=0. Nesse caso, temos o vetor normal n′ (E′,′,′) plano de P′ e o vetor normal n″ (E″,″,″) plano de P″. Já que nossos planos não são paralelos e não são iguais, então estes vetores não são collinear. Usando a linguagem da matemática, temos esta condição podemos escrever assim: n′≠ n″ ↔ (E′,′,′) ≠ (λ*E″,λ*″,λ*″), λϵR. Deixe direta, que se encontra na intersecção de N′ e N″ será designado pela letra e, neste caso, e = N′ ∩ N″.
– é uma linha reta, que consiste do conjunto de todos os pontos (comum) dos planos de P′ e N″. Isso significa que as coordenadas de qualquer ponto pertencente a uma reta e, têm que satisfazer a equação de E′x+′+′z+D′ a=0 e E″x+″+″z+D″ a=0. Significa o ponto de coordenadas será privado de solução do seguinte sistema de equações:
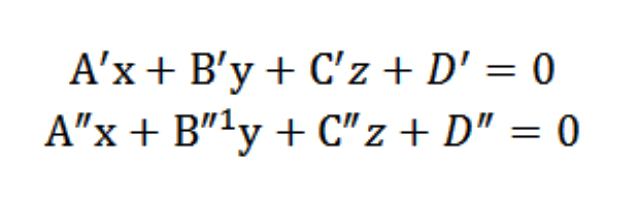
O resultado é que a decisão (total) este sistema de equações irá determinar as coordenadas de cada um dos pontos de uma reta, que será um ponto de intersecção de N′ e N″ e definir uma reta e no sistema de coordenadas Oxyz (retangular) no espaço.
Article in other languages:

Alin Trodden - autor do artigo, editor
"Olá, sou o Alin Trodden. Escrevo textos, leio livros e procuro impressões. E eu não sou ruim em falar sobre isso. Estou sempre feliz em participar de projetos interessantes."
Notícias Relacionadas
Catherine 2: a biografia de imperatriz. A História Da Rússia
Ambígua personalidade foi Catherine 2 Grande – a imperatriz russa de origem alemã. Na maioria dos artigos e filmes, em que ela mostra como o bebedor de cortesãos bailes e luxuosos banheiros, bem como de uma variedade de favo...
Espanhol império: descrição, história e bandeira
Espanhol império durante a época do seu poder foi um dos maiores estados, que já existiu no mundo. Criando um olhar relacionada com a era dos descobrimentos, quando tornou-se um poder colonial. Durante vários séculos, a bandeira d...
Os grupos temáticos palavras: exemplos
o Que é a unidade de russo? Certamente, a palavra. Com a ajuda dele nós nos comunicamos, compartilhamos uns aos outros os pensamentos e experiências. O artigo aborda a temática do grupo de palavras que permitem classificar a rique...
"Dizer" ou "diga-me": assim como ainda a escrever corretamente?
A pergunta sobre como escrever corretamente a palavra de deus: "dizer" ou "diga", podemos responder que ambas as opções têm o direito de existir, mas apenas no caso em que esses verbos estão em diferentes morfo...
O país mais populoso do mundo. Mônaco: fatos interessantes sobre o principado de
a Humanidade é extremamente desigualmente distribuída sobre a superfície de nosso planeta. Por exemplo, na pequena área asiática de estado, pode ficar mais de pessoas do que em todo o continente da Austrália. Onde está o país mais...
O que é ледостав: a definição do conceito e suas principais características
Rio – não é apenas водоток, несущийся com montanhas e elevações em mares e oceanos. É bastante complexo ecossistema, uma espécie de "corpo", o qual tem suas próprias características e modos. Que trata este artigo i...





















Comentários (0)
Este artigo possui nenhum comentário, seja o primeiro!