Now - 17:15:03
Equation of a plane: how to make? Types of equations of a plane
The space plane can be set in different ways (one point and a vector, two points and a vector, three points, etc.). With that in mind, the equation of the plane can have different types. Also, subject to certain conditions, the plane can be parallel, perpendicular, intersecting, etc. and talk About this in this article. We will learn how to get a General equation of a plane and not only.
Normal equations
For example, there is a space R3, which has a rectangular coordinate system XYZ. We define the vector α, which will be released from the initial point O Through the end of the vector α draw a plane P which is perpendicular to him.
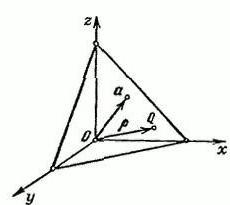
Denote by P an arbitrary point Q=(x,y,z). The radius-vector of point Q will sign the letter R. the length of the vector α is equal to R=IαI and Ʋʋ=(cosα cosβ cosγ).
This is a unit vector that is directed in the direction as the vector of α. α, β and γ – angles formed between a vector Ʋʋ and positive directions of the axes of space x, y, z, respectively. The projection of any point on QϵП Ʋʋ vector is constant, which is equal to R: (p,Ʋʋ) = p(p≥0).
The Specified equation makes sense when R=0. The only plane P in this case will cross the point (α=0), which is the origin, and unit vector Ʋʋ fired from point O perpendicular to P, despite its direction, which means that the Ʋʋ vector is determined up to sign. The preceding equation is the equation of our plane P is expressed in vector form. But in the coordinates it will look like this:
Recommended
"Knowledge is light and ignorance is darkness": the value, meaning and alternatives
There are some sayings that would seem to need no explanation, such as “teaching & ndash; light and ignorance – darkness”. But some still do not understand their meaning. But not only for such people is written by our article. I...
What was invented by Mendeleev for the army. The history and fate of the invention
D. I. Mendeleev was a brilliant Russian scientist-polymath, who made many important discoveries in various fields of science and technology. Many people know that he is the author of “Fundamentals of chemistry" and the periodic law of chem...
The origin of the Slavs. The influence of different cultures
Slavs (under this name), according to some researchers, appeared in the story only in 6 century ad. However, the language of nationality bears the archaic features of the Indo-European community. This, in turn, suggests that the origin of the Slavs h...
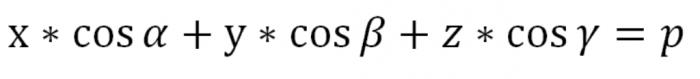
Here, R is greater than or equal to 0. We found the equation of a plane in space in the normal form.
General equations
If the equation in the coordinates multiply by any number that is not zero, we will obtain the equation, this is equivalent to specifying the same plane. It will look like this:
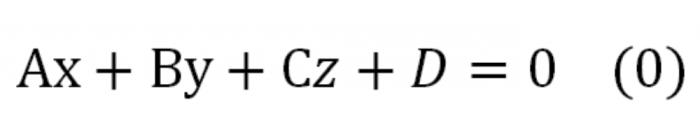
Here A, b, C – this is the number of simultaneously different from zero. This equation is referred to as the equation of a plane the General form.
Equations of planes. Special cases
The Equation in General form can be modified with additional conditions. Consider some of them.
Suppose that a coefficient is equal to 0. This means that the given plane is parallel to the ox axis. In this case, the equation will change: vu+Cz+D=0.
Similarly, the equation will change under the following conditions:
- First, if=0, then the equation will change to ax+Cz+D=0, which would indicate parallel to the axis Oy.
- Second, if C=0, the equation is converted to Oh+Wu+D=0, which will speak about the parallel to a given axis Oz.
- Third, if D=0, the equation will look like ax+Wu+Cz=0, which would mean that the plane intersects O (origin of coordinates).
- Fourth, if A=B=0, the equation will change to Cz+D=0, which will prove a parallel to Oxy.
- Fifth, if B=C=0, the equation becomes ax+D=0, and this means the plane parallel to Oyz.
- Sixth, if A=C=0, the equation will take the form vu+D=0, that is, will report parallel to Oxz.
Form of the equation in segments
In the case when the numbers A, b, C, D are nonzero, the equation (0) can be as follows:
X/a + y/b + z/C = 1
In which a = -D/A, b = -D/, C = -D/S.
The Resulting equation of the plane in segments. It should be noted that this plane will cross the axis ox at the point with coordinates (a,0,0), Oh – (0,b,0), and Oz – (0,0,C).
Given the equation x/a + y/b + z/C = 1 it is easy to visualize the location of the plane relative to the defined coordinate system.
The coordinates of the normal vector
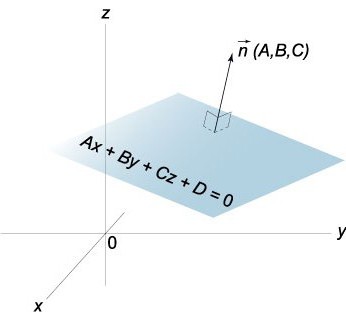
The Normal vector n to the plane P has coordinates that are the coefficients of the General equation of this plane, that is, n (A,b,C).
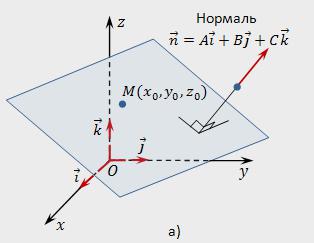
To determine the coordinates of the normal n, it is enough to know the General equation of the given plane.
When using the equation in segments, which has the form x/a + y/b + z/C = 1, as in the General equation, we can write the coordinates of any normal vector to a given plane: (1/a + 1/b + 1/C).
It is Worth noting that the normal vector helps to solve a variety of problems. The most common are objective proof of perpendicularity or parallelism of the surfaces, the task of finding the angles between the planes or angles between planes and straight lines.
Form of the equation of the plane according to the coordinates of the point and normal vector
A Nonzero vector n perpendicular to the specified plane, called normal (normal) for the given plane.
Suppose that in the coordinate space (rectangular coordinate system) Oxyz is specified:
- Point Mo with coordinates (хₒ,уₒ,zₒ);
- Zero vector n=A*i+A*j+C*k.
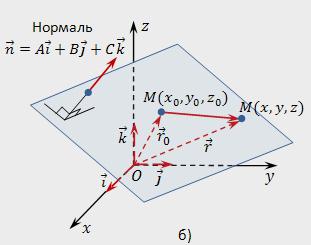
We Need to write the equation of the plane which will pass through the point Mo is perpendicular to the normal n.
In the space we choose any arbitrary point and denote it M (x,z). Letthe radius-vector of any point M (x,y,z) is r=x*i+y*j+z*k, and the radius-vector of the point Mo (хₒ,уₒ,zₒ) – rₒ=хₒ*i+уₒ*j+zₒ*k. Point M will belong to the specified plane, if the vector of the IOM will be perpendicular to the vector n. Write the condition of orthogonality using the dot product:
[IOM, n] = 0.
Since MΩ = r– rₒ, vector equation of a plane will look like this:
[r-rₒ, n] = 0.
This equation may have different shape. For this purpose, the properties of the scalar product, and is converted to the left side of the equation. [r-rₒ, n] = [r, n] – [rₒ, n]. If [rₒ, n] denote by C, we get the following equation: [r, n] - C = 0 or [r, n] = C, which expresses the constancy of the projections on the normal vector of the radius-vectors of the given points that belong to the plane.
It is Now possible to coordinate the record vector equation of our plane [r-rₒ, n] = 0. Since r–rₒ = (x–хₒ)*i + (–уₒ)*j + (z-zₒ)*k and n = A*i+A*j+C*k, we have:
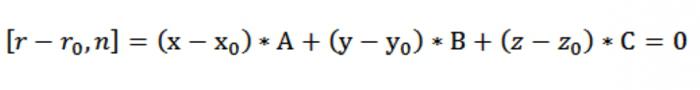
So, we have formed the equation of the plane passing through the point perpendicular to normal n:
A*(x - хₒ)+*(– уₒ)*(z-zₒ)=0.
Form of the equation of the plane according to the coordinates of two points and a vector, collinear to the plane
We Define two arbitrary points M′ (x′,′,z′) and M″ (x″,″,z″) and a vector a (a′ and″,and").
Now we can write the equation of the given plane which will pass through the point M′ M″, and any point M with coordinates (x,y,z) parallel to a specified vector.
The vectors in M′M={x-x′, t′;z′} M″M={x″ x′;u″-y′ z″ z′} must be coplanar with the vector a=(a′ and″,and"), which means (M′M″M, a)=0.
So, our equation of plane in space will look like this:
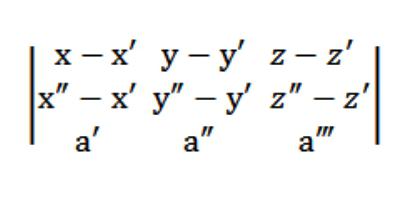
Form of the equation of the plane that intersects three points
Suppose we have three points: (x′,′,z′), (x″,″,z″), (x",y",z") that do not belong to one straight line. You must write the equation of the plane passing through the specified three points. The theory of geometry asserts that such a plane does exist, except she's the one and only. Since this plane intersects the point (x′,′,z′), its equation will be as follows:
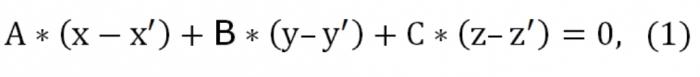
Here A, b, C different from zero at the same time. Also the given plane intersects two points: (x″,″,z″) and (x",y",z"). In this connection it should be performed such conditions:
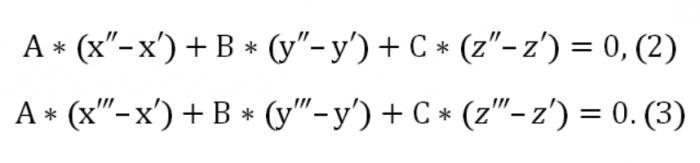
Now we can write down a homogeneous system of equations (linear) with unknown u, v, w:
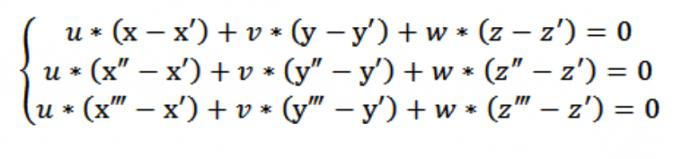
In our case x,y or z acts arbitrary point that satisfies equation (1). Given equation (1) and the system of equations (2) and (3) the system of equations shown on the figure above, satisfies the vector N (A,b,C), which is non-trivial. This is because the determinant of this system equal to zero.
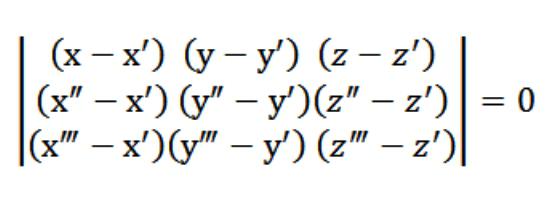
Equation (1), which we did, this is the equation of the plane. 3 point it definitely is, and it's easy to check. For this you need to lay out our keys to the elements in the first row. Of the existing properties of the determinant it follows that our plane simultaneously intersects the three originally given points (x′,′,z′), (x″,″,z″), (x",y",z"). So we decided the task set before us.
Dihedral angle between planes
The Dihedral angle is a spatial geometric figure formed by two half-planes that originate from the same line. In other words, this part of the space, which is restricted to these half-planes.
Suppose we have two planes with the following equations:
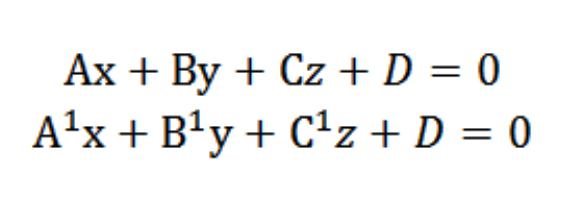
We know that the vectors N=(A,b,C) and N¹=(A¹¹,¹) are perpendicular according to the specified planes. In this regard, the angle &phi between vectors N and N¹ is equal to the angle (dihedral), which is located between these planes. The scalar product has the form:
NN¹=|N||N¹|cos φ
Just because
Cosφ= NN¹/|N||N¹|=(a¹+W¹+SS¹)/((√(A²+B²+S²))*(√(A¹)²+(V¹)²+(S¹)²)).
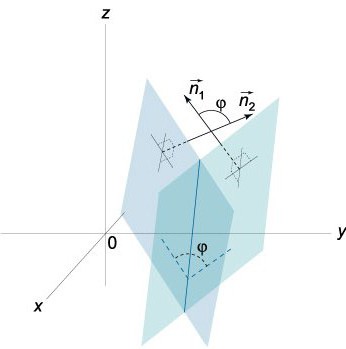
It is Enough to note that 0≤φ≤π.
Actually two planes that intersect to form two angles (dihedral): φ1 and φ2. The sum of them is equal to π (φ1+ φ2= π). As for their cosines, their absolute values are equal, but they differ in signs, that is, cos φ1=-cos φ2. If the equation (0) to replace A, b and C the numbers A, -b and -C, respectively, then the equation that we get will determine the same plane, only the angle φ in the equation cos φ= NN1/|N||N1| will be replaced by π-φ.
The equation of the perpendicular to the plane
Called Perpendicular plane, between which the angle is 90 degrees. Using the material presented above, we can find the equation of a planeperpendicular to the other. Let's say we have two planes: ax+Wu+Cz+D=0 and A¹x¹+¹z+D=0. We can say that they will be perpendicular if cosφ=0. This means that NN¹=AA¹+BB¹+SS¹=0.
The equation of the parallel plane
Referred to as two Parallel planes which do not contain common points.
The Condition of parallelism of planes (their equations are the same as in the previous paragraph) is that the vectors N and N¹ they are perpendicular, collinear. This means that the following conditions of proportionality:
A/A¹=/¹=/¹.
If the conditions of proportionality are extended to A/A¹=/¹=/¹=DD¹
This indicates that the data plane are the same. This means that the equation ax+Wu+Cz+D=0 and A¹x¹+¹z+D¹=0 describe the same plane.
The distance to the plane from a point
Suppose we have a plane P which is given by the equation (0). You need to find the distance between a point with coordinates (хₒ,уₒ,zₒ)=Qₒ. To do this, you need to give the equation of the plane P in a normal form:
(ρ v)=p (p≥0).
In this case ρ (x,y,z) is the radius vector of our point Q, located at P, R & ndash; is the length of the perpendicular P, which was released from the zero point, v – is a unit vector that is in the direction.
The ρ-ρº the radius vector of any point Q=(x,y,z) belonging to P, and the radius-vector of a given point Q0=(хₒ,уₒ,zₒ) is such a vector, the absolute value of the projection of which in v equals the distance d, which need to be found from Q0=(хₒ,уₒ,zₒ) to P:
D=|(ρ-ρ0,v)|, but
(ρ-ρ0,v)= (ρ v)–(ρ0,v) =R - (ρ0,v).
So,
D=|(ρ0,v)-R|.
Now you can see to calculate the distance d from Q0 to the plane P, it is necessary to use normal equations of a plane, to transfer to the left side of R, and the last is x,y,z to substitute (хₒ,уₒ,zₒ).
Thus, we find the absolute value of the resulting expression, d is the sought.
Using the language of the parameters obtained are obvious:
D=|AXO+Vuo+Czₒ|/√(A²+²+C²).
If the specified point is Q0 is on the other side of plane P as the origin, vector ρ-ρ0 and v is an obtuse angle, thus:
D=-(ρ-ρ0,v)=(ρ0,v)-R>0.
In the case when the point Q0 together with the origin of coordinates is located at the same side of P, the created angle is sharp, that is:
D=(ρ-ρ0,v)=R - (ρ0, v)>0.
The result is that in the first case (ρ0,v)>R in the second (ρ0,v)<R.
Tangent plane and its equation
On the plane to the surface at the tangent point Mº – this is the plane containing all possible tangents to curves, drawn through this point on the surface.
In this form of the equation of the surface F(x,y,z)=0 the equation of the tangent plane at a tangent point Mº(xº,º,zº) will look like this:
FX(xº,º,zº)(x - xº)+ FX(xº,º, zº)(u - uº)+ FX(xº,º,zº)(z-zº)=0.
If you specify a surface in an explicit form z=f (x,y), the tangent plane will be described by the equation:
Z-zº =f(xº,º)(x - xº)+f(xº,º)(u - uº).
The Intersection of two planes
In three-dimensional space is a system of coordinates (rectangular) Oxyz, given two planes P′ P″, which intersect and do not coincide. Because any plane in the rectangular coordinate system, is determined by the General equation, we assume that P′ P″ are defined by equations of A′x′y′z+D′=0 And″x″y″z+D″=0. In this case, we have a normal n′ (I′,′,′) - plane, P′ and normal n″ (I″,″,″) - plane, P″. Since our planes are not parallel and do not coincide, then these vectors are not collinear. Using the language of mathematics, we this condition can be written as: n′≠ n″ ↔ (A′,′,′) ≠ (λ*And″,λ*″,λ*″), λϵR. Let the straight line which lies at the intersection of the P′ P″, will be denoted by the letter a, in this case a = P′ ∩, P″.
And – video consisting of the set of all points (total) planes of the P′ P″. This means that the coordinates of any point belonging to a straight line and must simultaneously satisfy the equations of A′x′y′z+D′=0 And″x″y″z+D″=0. So, the coordinates of the point will be the private solution of the following system of equations:
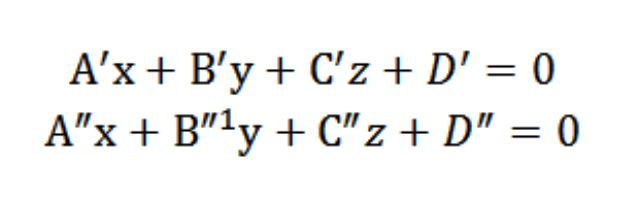
In the end, it turns out that the solution to (common) this system of equations will determine the coordinates of each point of the line, which will act as the point of intersection of the P′ P″, and determine the line and in a coordinate system Oxyz (rectangular) in space.
Article in other languages:

Alin Trodden - author of the article, editor
"Hi, I'm Alin Trodden. I write texts, read books, and look for impressions. And I'm not bad at telling you about it. I am always happy to participate in interesting projects."
Related News
Where to hide a cheat sheet: the best ideas for brave students
In the life of student is all. You will come across a teacher, especially to create conditions for bribes, the list of topics for the exam are issued for three days before his passing, the course requires accurate knowledge and in...
the human Skull is the skeleton of his head. Divided the bone on the facial and cerebral parts. In the brain region skeleton head in the form close to the ball. Part this part consists of two parietal, frontal, occipital, two temp...
The technology of developing training
In view of the rapid technologization of the educational process the advanced ideas of training and education couched in the form of technology. One of the recognized is technology developmental education. Psychologica...
Obtuse triangle: length of sides, sum of angles. Described obtuse-angled triangle
Even preschool children know what it looks like a triangle. But what they are, the guys are beginning to understand in school. One type is an obtuse triangle. To understand what it is, the easiest way, if you see the picture with ...
oil Reserves in the world can be estimated on the basis of various indicators. However, today they are determined by the number of extracted raw materials, which allows to extract at the moment the current level of technology and ...
How to finish letters correctly
How often have to write letters? Many use electronic and conventional mail services for sending mass notifications to send business emails from a corporate email or formal request to state bodies. To write a good letter is only ha...






















Comments (0)
This article has no comment, be the first!