How to solve inequality? How to solve fractional and quadratic inequalities?
The Concept of mathematical inequality originated in ancient times. It happened when primitive man felt the need at halftime and actions with different objects to compare their number and size. Since the ancient times and of the inequalities used in his reasoning, Archimedes, Euclid, and other celebrated scientists: mathematicians, astronomers, designers, and philosophers.
But they, as a rule, used in his work verbal terminology. The first modern signs to represent the concepts of “more” and “less”, which they today every schoolchild knows, invented and applied in practice in England. Favour of the descendants of the mathematician Thomas Harriot. And it happened nearly four centuries ago.

There are many types of inequalities. Among them are simple, containing one, two or more variables, quadratic, fractional, complex relationships and even represented by a system of expressions. But to understand how to solve inequalities, it is best to various examples.
Don't miss the train
To begin, let us imagine that a resident of a rural area in a hurry at the train station, which is located at a distance of 20 km from his village. In order not to miss the train, departing at 11 o'clock, it is time to leave the house. What time it must be done, if its speed is 5 km/h? The solution to this practical problem is reduced to the expression: 5 (11-X) ≥ 20, where X-the time of departure.
This is understandable, because the distance that must be overcome villager station is equal to the speed multiplied by the number of hours. To reach before the person can, but that's to be late he does not. Knowing how to solve the inequality, and applying their skills in practice, in the end we get X ≤ 7, and that is the answer. This means that the peasants should go to the train station at seven in the morning or a little earlier.
Numeric intervals on the coordinate axis
Now let's figure out how to display the described ratios on the coordinate axis. The above inequality is not strict. It means that the variable can take values less than 7, and can be equal to this number. We give other examples. To do this, look carefully at the four figures below.
Recommended
"Knowledge is light and ignorance is darkness": the value, meaning and alternatives
There are some sayings that would seem to need no explanation, such as “teaching & ndash; light and ignorance – darkness”. But some still do not understand their meaning. But not only for such people is written by our article. I...
What was invented by Mendeleev for the army. The history and fate of the invention
D. I. Mendeleev was a brilliant Russian scientist-polymath, who made many important discoveries in various fields of science and technology. Many people know that he is the author of “Fundamentals of chemistry" and the periodic law of chem...
The origin of the Slavs. The influence of different cultures
Slavs (under this name), according to some researchers, appeared in the story only in 6 century ad. However, the language of nationality bears the archaic features of the Indo-European community. This, in turn, suggests that the origin of the Slavs h...
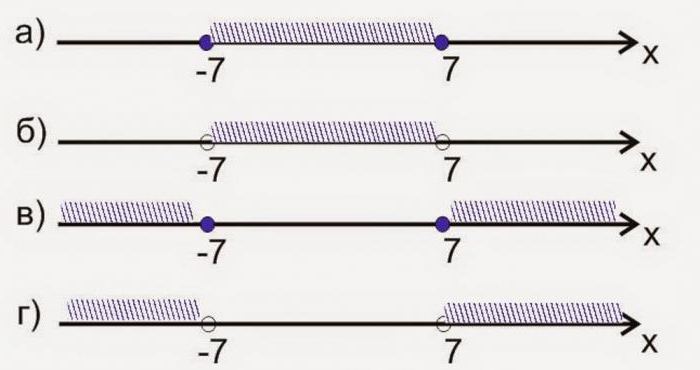
The first of them you can see a graphic image of the interval [-7; 7]. It consists of a set of numbers placed on the coordinate axis and located between -7 and 7, including the border. In this case the data points are shown as filled circles, and the recording interval is done using square brackets.
The Second figure is a graphical representation of strict inequalities. In this case, the edge numbers are -7 and 7, shown punctured (not shaded) points are not included in the specified set. A record of the period is in parentheses as follows: (-7; 7).
That is, finding out how to solve inequalities Of this type, and received a similar response, we can conclude that it consists of numbers contained between these boundaries, except -7 and 7. The following two cases need to be assessed in the same way. On the third picture are the images of the intervals (-∞; -7] U [7; +∞) and the fourth (-∞; -7) U (7; +∞).
Two expressions in one
You can Often find the following entry: 7 < 2 – 3 < 12. How to solve a double inequality? This means that on expression imposed two conditions. And each of them should be taken into account to obtain the correct answer for the variable X. Taking into account this situation, we obtain from relations 2 – 3 > 7 and 2 – 3 < 11
5 < X < 7. The final answer is recorded thus: (5; 7). This means that the variable takes many values that are enclosed in the interval between the numbers 5 and 7, except for the border.
Similar properties with the equation
An Equation is an expression that combine the sign = , which means that both parts of it (left and right) are identical in size. So often these relationships linked with the image of vintage scales with bowl mounted and fastened by means of a lever. This device is always in equilibrium, if both ends have the same weight. The position is not changed if the left and right sides are padded or lose the goods of the same mass.

In a mathematical equation to both sides of this equality that it has not violated, is also possible to add the same number. It may be positive or negative. How to solve inequalities in this case, and whether you can do the same with them? The previous examples showed that, Yes.
Contrast to equations
Both parts of the expression connected by the signs < or > you can multiply and divide by any positive number. The true ratio is not disturbed. But how to solve inequality with fractions and negative integers multipliers, preceded by a minus sign? Here the situation is quite different.
Let us Examine this with an example: -3X < 12. To highlight a variable in the left part, we have to divide each by -3. In this case the inequality sign is reversed. Get X > -4, what is the answertasks.
Interval methods
Inequality is called quadratic if it contains a variable raised to the second power. An example of such a relationship may serve the following expression: X2 – 2 + 3 > 0. How to solve quadratic inequalities? The most convenient method is the method of intervals. For implementation of the plan should be to factorize the left part of the ratio. Is obtained: (X-3)(X + 1). Then it is recommended to find the zeros of the function and place the resulting points in the correct order on the coordinate axis.
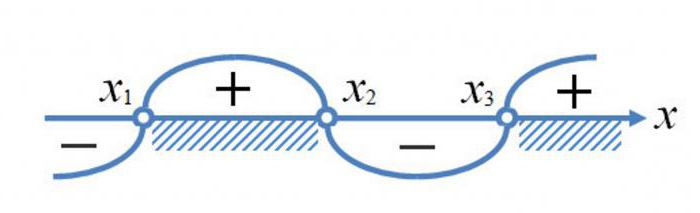
Next you need to allocate the signs of the resulting intervals, substituting in the expression any of the numbers that belong to the given interval. While in simple cases it is usually enough to understand at least one of them, and the rest set according to the rule of alternation. In conclusion, it remains only to select the appropriate intervals to obtain the final decision.
Square inequality here obey the law of correspondence of the negative areas cons, and a positive advantages. That is, if the expression is greater than zero, you should take the numeric intervals are marked with + . And in the opposite case, the solution will be areas marked with - . Thus, the solution to our inequality can be written as: (-∞; -1) U (3; +∞).
Other examples of applying the method of intervals
The Described method gives the answer to another important question: how to solve fractional inequalities, if this case is applicable the same method intervals? Let us consider how this can be done, for example relations presented below.
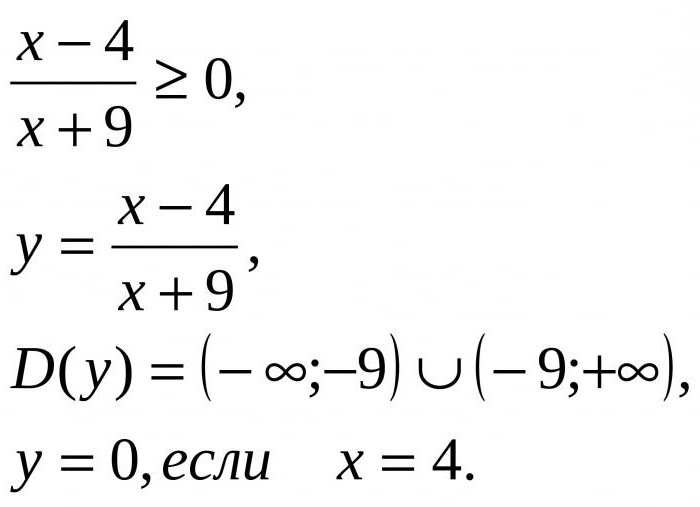
Here the zeros of the function are points -9 and 4. For finding the solution should be applied to them to coordinate direct and determine the signs of the intervals, selecting those that will be marked with a plus sign. It should be note that the shaded is only the number 4.
Another point bude punctured, since -9 is not included in the range of values that are valid. Indeed, while in the denominator turns zero that in mathematics impossible. How to solve fractional inequalities? In this case, the final answer will be the Union of the intervals: (-∞; -9) U [4; +∞).
Parabolas on a graph
Find Out all about the inequalities often help not only figures on the coordinate axis, but the image in the Cartesian plane. The graph of the quadratic dependence, as is known, is a parabola. Even a schematic drawing of this type is able to give answers to questions. Consider some of the kinds of parabolas, giving an idea about the solution of quadratic inequalities.
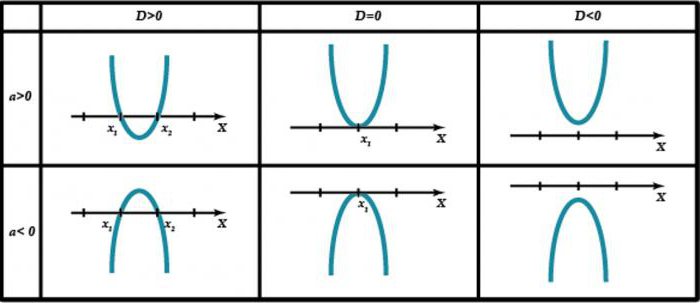
Here, first of all understand certain truths. Any expression of this type is to mind: Oh2 + BX + C = 0. In this case, if a coefficient is positive, then the parabola to draw branches the top, in case the opposite – down. But the roots of the equation are the points where the intersection of the function with the axis OX.
Interpretation
Know the above statements are very important for understanding of square inequalities, and responses to questions associated with them. Draw a diagram of a parabola on a Cartesian plane, to solve you need to find out what time a function (that is, values of coordinates of points on the axis Oy) takes the indices + and -. Thus, if the inequality sign is>, then his decision is the set of values taken by variable X at positive U.
In the case of the < indicates the indicators to X at negative U. it Happens that the parabola does not intersect with the axis OX. This happens in cases where D < 0. Then, if the graph is in the upper half plane, the answer to the quadratic inequality with a sign > will be the interval (-∞; +∞). And < solution is the empty set. With the lower half-plane, the situation is exactly the opposite.
About the use of graphic images
The Image on a Cartesian plane substantially facilitate the task for systems of equations. The drawings clearly show solutions that are points of intersection of the marked lines. It remains only to calculate their coordinates and record the response.
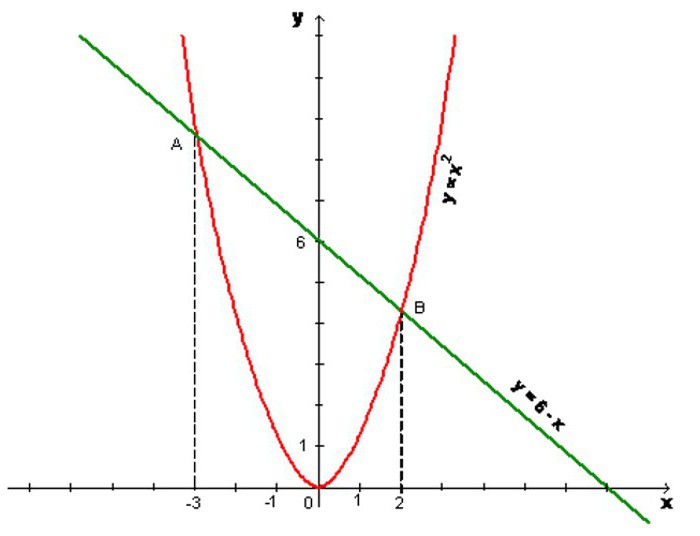
The same applies to inequalities. For example, the decision of the ratio u ≤ 6 – x (as is clear in the picture) is itself a direct y = 6 - x, as well as the half-plane below the boundary. For exact answer, you can take any point on the graph (e.g. (1; 3) and substitute its coordinates into the inequality. We obtain: 3 ≤ 6 - 1, that is the correct ratio. So, the above argument was true.
The Inequality u ≥ x2 describes a region in the Cartesian plane located in the bowl of a parabola, including its borders. And at the intersection of these sectors we can find a solution of a ratio written in the form: x2 ≤ I ≤ 6 – H. It will be limited to the bottom line of the parabola and the top to be clipped straight. For sure will do again the test, substituting the coordinate values of any point, since to this region.
Take (1; 4). Get: 1 ≤ 4 ≤ 6 - 1, i.e., again the right balance. Here again there is a sense to note that inequality has many similar features with the equations, albeit endowed with significantdifferences.
Article in other languages:

Alin Trodden - author of the article, editor
"Hi, I'm Alin Trodden. I write texts, read books, and look for impressions. And I'm not bad at telling you about it. I am always happy to participate in interesting projects."
Related News
the School prom-an event that will definitely be remembered for a lifetime. It's not just parting with the school, it is also the separation from friends and the unknown that frightens and attracts at the same time former students...
Conclusion on production practice at the enterprise: example
While teaching a variety of qualifications in the curriculum lays a large number of practical sessions, where students are required to experience the charm of the received profession. As the report future specialists and bachelors...
Lability - what is it? The value of the concept in medicine and psychology
You probably have heard the word “liability”. What does it mean? Where used this term? He came from the Latin labilis, which means “rolling” or “unsustainable”. For the first time this concept w...
Gydansky Peninsula: the field, the climate, the territory. Reserve on the Gydan Peninsula
gydansky Peninsula with a harsh climate, the famous oil and gas fields. But not only that. Its territory is a nature reserve. What animals live on land and in the sea that grows there, read the article.Where is the gydansky Penins...
The Stirling engine principle of operation. Low temperature Stirling engine (photo)
the Stirling Engine, which is qualitatively different from the usual for all the engines, once was the last decent competition. However, at some time forgot about it. As this motor is used today, what is the principle of its actio...
the Conflict between Egypt and Israel has been brewing long before the events of June 1967. This time was a turning point in Israel's history. The six-day war lasted from 5 to 10 June and brought unexpected results for both partie...






















Comments (0)
This article has no comment, be the first!